决策树是一种常见的机器学习算法,既能做分类,也能做回归,不过大多数情况用决策树来解决分类问题。决策树算法是以树状结构来表示数据的分类结果。一般来说,一颗决策树包含一个根节点,若干个非叶子节点和若干个叶子节点
决策树
信息熵和信息增益
在热力学中,熵表示着物质的混乱程度,在计算机领域中,信息熵越大表示越混乱,表示该数据集越不纯净,类别越多,反之亦然。而我们构造决策树的基本思想就是,在非叶子节点中选择合适的条件,使得其子孙节点的熵尽可能的低(分类结果尽可能纯净),且树的深度还要比较短(速度快)。熵的计算公式如下:
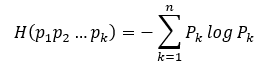
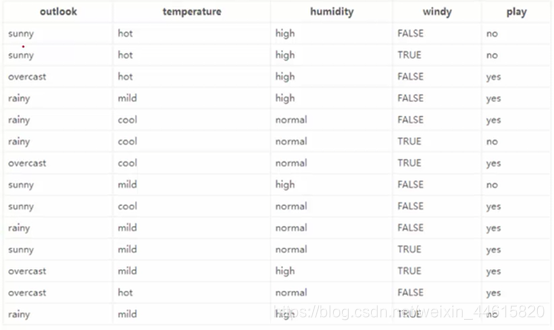
我们要判断今天是否打球(play),用下图数据为例:
从play这一栏看到,play的概率是9/14,no-play的概率是5/14,那么此时的熵就为: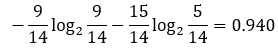
我们记 H(Play)=0.940H(Play)=0.940H(Play)=0.940 为原始熵。
如果要基于某个条件(事件)计算某个事件的熵,该熵就成为条件熵,条件熵表示为:
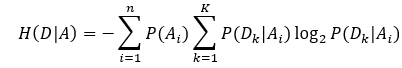
P(Ai)P(A_i)P(Ai)表示A事件的第iii种值对应的概率。
就以Outlook来看,其有三个label:sunny(5/14)、rainy(5/14)、overcast(4/14)。在sunny条件下,打球的概率为2/5,不打球的概率为3/5,此时熵为0.971,同理可求rainy=0.971,overcast=0(因为打球概率100%,不打球概率为0)。所以当基于outlook计算是否打球这个事件,
H(Play∣Outlook)=−5/14∗0.971−0−5/14∗0.971=0.694H(Play|Outlook)=-5/14*0.971-0-5/14*0.971=0.694H(Play∣Outlook)=−5/14∗0.971−0−5/14∗0.971=0.694
同理可求其他几个变量对因变量Play的条件熵为:
H(Play∣Tempreture)=0.911H(Play|Tempreture)=0.911H(Play∣Tempreture)=0.911
H(Play∣Humidiy)=0.789H(Play|Humidiy)=0.789H(Play∣Humidiy)=0.789
H(Play∣Windy)=0.892H(Play|Windy)=0.892H(Play∣Windy)=0.892
那么我们要如何选择哪个变量为根节点呢?这里就要涉及到信息增益这个概念。决策树在构建过程中,从根节点到叶子节点,信息熵是下降的过程,这个下降的量,就为信息增益。在根节点或内部节点的变量选择中,选择信息增益最大的的变量为判断条件,这样能使得熵值下降的最快,分类结果最纯净。
上述几个变量的信息增益为:
GainOutlook(Play)=H(Play)−H(Play│Outlook)=0.246Gain_{Outlook}(Play)=H(Play)-H(Play│Outlook)=0.246GainOutlook(Play)=H(Play)−H(Play│Outlook)=0.246
GainTempreture(Play)=H(Play)−H(Play│Tempreture)=0.029Gain_{Tempreture}(Play)=H(Play)-H(Play│Tempreture)=0.029GainTempreture(Play)=H(Play)−H(Play│Tempreture)=0.029
GainHumidiy(Play)=H(Play)−H(Play│Humidiy)=0.151Gain_{Humidiy}(Play)=H(Play)-H(Play│Humidiy)=0.151GainHumidiy(Play)=H(Play)−H(Play│Humidiy)=0.151
GainWindy(Play)=H(Play)−H(Play│Windy)=0.0.048Gain_{Windy}(Play)=H(Play)-H(Play│Windy)=0.0.048GainWindy(Play)=H(Play)−H(Play│Windy)=0.0.048
所以选择Outlook作为根节点。
基尼系数
基尼系数和信息增益类似,其表达式为:
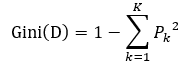
根据基尼系数下降的快慢ΔGini(D)=Gini(D)−GiniA(D)ΔGini(D)=Gini(D)-Gini_A(D)ΔGini(D)=Gini(D)−GiniA(D)来选择根节点或内部节点。
我们还是以是否打球为例,根据基尼系数来选择其根节点。
【回宿舍算吧】
信息增益率
如果单单采用比较信息增益来选择根节点或内部节点就会面临一个问题,当分支节点非常多,且每个AiA_iAi仅包含一个样本(或极少),这种分支节点的纯度将很高,比如将数据编号(1,2,3…)也加入数据集进行分类,那编号的信息增益将会远大于其他变量,很显然这不能真实的反映分类结果。比如有1000个样本,有一个特征,这个特征有100个判别级别,这一个特征正好就可以将所有的样本划分完成,直接分成了100个子节点。为了避免这种情况的发生,引入了信息增益率。
信息增益率=信息增益/自身的熵
如果在分类数据集中各自变量的取值个数没哟太大差异,那么信息增益率和信息增益其实没有太大差异。
剪枝
剪枝是决策树中一个很关键的概念。只要树的深度足够深,其实是可以将每个数据都分类来,但这样岂不是过拟合了,所以在合适的时候就有必要进行剪枝。剪枝分为预剪枝和后剪枝。预剪枝即在决策树生长过程中,提前结束或者限制其节点个数。
后剪枝则是在决策树生成以后再剪枝。那么该怎么剪将是一个大问题,剪枝后的结果要对决策树的损失最小,所以通常采用极小化损失函数。
损失函数表达式如下:
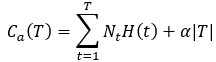
∣T∣|T|∣T∣为节点T所对应叶结点个数,t是节点T下第t个叶结点,NtN_tNt为第t叶节点的样本数,H(t)H(t)H(t)是第t个叶节点的信息熵,α是调节参数,可以手动设置。
其中的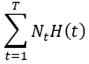 也称评价函数,写做C(T)C(T)C(T)。对比节点T剪枝前的损失函数(Ca(T)before)(C_a(T)_{before})(Ca(T)before),和剪枝后的损失函数(Ca(T)after)(C_a(T)_{after})(Ca(T)after),若Ca(T)after≥Ca(T)beforeC_a(T)_{after}≥C_a(T)_{before}Ca(T)after≥Ca(T)before,则把父节点做为新的叶节点。循环这个步骤,知道得到损失函数最小的子树TaT_aTa
也称评价函数,写做C(T)C(T)C(T)。对比节点T剪枝前的损失函数(Ca(T)before)(C_a(T)_{before})(Ca(T)before),和剪枝后的损失函数(Ca(T)after)(C_a(T)_{after})(Ca(T)after),若Ca(T)after≥Ca(T)beforeC_a(T)_{after}≥C_a(T)_{before}Ca(T)after≥Ca(T)before,则把父节点做为新的叶节点。循环这个步骤,知道得到损失函数最小的子树TaT_aTa
下面泰坦尼克号船员获救的数据集为例
导入模块和数据集
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
titanic_=pd.read_csv('C:\\Users\\HP\\Titanic\\train.csv')
titanic_.head()
前五行如下:

查看缺失值
print(titanic_.isnull().sum())
print('>>>>>>>>>>>>')
titanic_.Survived.value_counts().plot(kind='bar',title="Number of survivors and deaths")
泰坦尼克号船员获救我们知道和姓名、船票价格、船员标号等信息无关,但是假如面对的是未知的数据集,还是应该对每个特征进行分析的,找出对获救最主要的几个特征。以后把分析补上。。
#舍去无关变量
titanic=titanic_.drop(['PassengerId','Cabin','Name','Ticket'],axis=1)
titanic.head()
做一个简单的可视化
#统计男女人数
males=(titanic['Sex']=='male').sum()
females=(titanic['Sex']=='female').sum()
#统计比例
proportions=[males,females]
#创建饼图
plt.pie(proportions,labels=['Males','Females'],startangle=90,autopct='%1.1f%%',wedgeprops={'linewidth':20},textprops={'fontsize':20})
plt.axis('equal')
plt.title("Sex Proportion")
plt.tight_layout()
plt.show()
填补缺失值
titanic["Age"]=titanic["Age"].fillna(titanic["Age"].mean())
titanic["Embarked"]=titanic["Embarked"].fillna("S")
print(titanic.isnull().sum())

#Pclass,Sex,Embarked为数值型变量,将其转化为类别型,进行哑变量处理
titanic.Pclass=titanic.Pclass.astype('category')
#哑变量处理
dummy=pd.get_dummies(titanic[['Sex','Embarked','Pclass']])
#水平合并原数据集和哑变量
titanic=pd.concat([titanic,dummy],axis=1)
#删除为处理时时变量,保留哑变量
titanic.drop(['Sex','Embarked','Pclass'],inplace=True,axis=1)
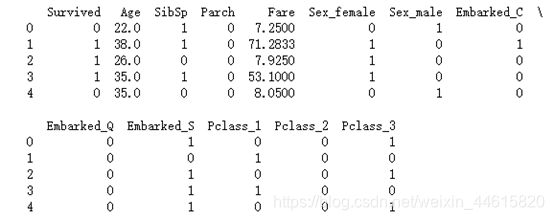
print(titanic.head())
处理后的输出结果如下:
#数据分割
predictors=titanic.columns[1:]
from sklearn.cross_validation import train_test_split
X_train,X_test,y_train,y_test=train_test_split(titanic[predictors],titanic['Survived'],test_size=0.3)
导入决策树
from sklearn.tree import DecisionTreeClassifier
dtc=DecisionTreeClassifier()
dtc.fit(X_train,y_train)
y_predict=dtc.predict(X_test)
print(y_predict)
print("模型在测试集上的准确率为:",dtc.score(X_test,y_test))
模型在测试集上的准确率为: 0.7723880597014925
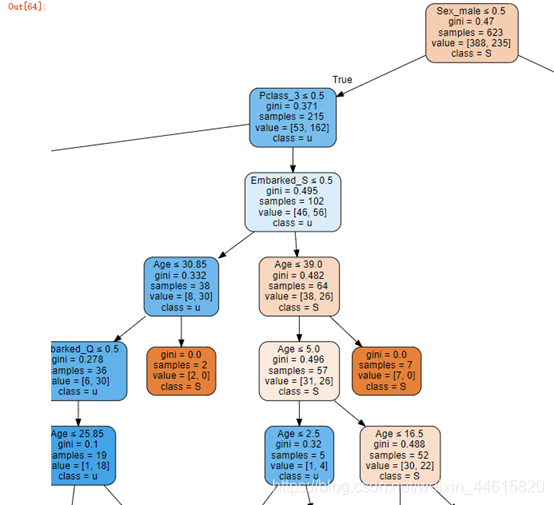
决策树的简单展现
import graphviz
dot_data = export_graphviz(dtc,out_file=None,feature_names=predictors,class_names="Survived",filled=True, rounded=True,special_characters=True)
graph = graphviz.Source(dot_data)
graph
























 1854
1854

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








