欧拉定理

一、欧拉函数的求法
证明及讲解
模版
直接求解欧拉函数

int oula(int n)
{
    int r=n;
    for(int i=2;i*i<=n;i++)
    {
        if(n%i==0)
        {
            r=r-r/i;
            do
            {
                n/=i;
            }
            while(n%i==0);
        }
    }
    if(n>1)
        r=r-r/n;
    return r;

}

欧拉性质
费马小定理 a^（p-1）≡1（mod p）
下面一道题就用到了费马小定理
要求(A/B)%9973，但由于A很大，我们只给出n(n=A%9973)(我们给定的A必能被B整除，且gcd(B,9973) = 1)。
Input
数据的第一行是一个T，表示有T组数据。
每组数据有两个数n(0 <= n < 9973)和B(1 <= B <= 10^9)。
Output
对应每组数据输出(A/B)%9973。
Sample Input
2
1000 53
87 123456789
Sample Output
7922
6060

（A/B%9973)=(AB^-1)%9973
根据费马小定理 B^9973-1=1(mod 9973）
BB^9973-2=1(mod 9973)
B^9973-2=(1/B)(mod 9973)
所以 (1/B)=B^9971%9973
所以原式=(A*B^9971%9973)%9973
用快速幂求出B^9971%9973即可

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <math.h>
#define ll  long long
using namespace std;
const  int maxn=1e7+10;
ll poww(ll a,ll b)//快速幂
{
    ll ans=1;
    while(b)
    {
        if(b&1)
            ans=ans*a%9973;
        a=a*a%9973;
        b>>=1;
    }
    return ans;
}
int main()
{
    int t;
    scanf("%d",&t);
    ll n;
    ll b;
    while(t--)
    {
        scanf("%lld%lld",&n,&b);
        ll ans=poww(b,9971);
        printf("%lld\n",n*ans%9973%9973);
    }
    return 0;

}

欧拉筛选

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <math.h>
#define ll  long long
using namespace std;
const  int maxn=1e7+10;
int vis[maxn];
int prime[maxn];
int num=0;
int n;
void pri()
{
    memset(vis,0,sizeof(vis));
    memset(q,0,sizeof(q));
    for(int i=2;i<=n;i++)
    {
        if(vis[i]==0)
        {
            prime[num++]=i;
        }

        for(int j=0;j<=num&&i*prime[j]<=n;j++)
        {
            vis[i*prime[j]]=1;
            if(i%prime[j]==0)
                break;//表明这个数已经被筛选过
        }
    }
}

频繁使用欧拉函数值，预先打表
可预先之所有数的欧拉函数值都为她本身。
有定理可知，如果p是一个正整数且满足φ（p）=p-1;那么p是素数，在遍历过程中如果遇到欧拉函数与自身相等的情况。
那么说明该数为素数，把这个数的欧拉函数值改变，同时也把能被素因子整除的数改变。

void oula()
{
    for(int i=2;i<maxn;i++)
        p[i]=i;//预先假设所有的欧拉函数值为本身自己
    for(int i=2;i<maxn;i+=2)
        p[i]/=2;
    for(int i=2;i<maxn;i++)
    {
        if(p[i]==i)
        {
            for(int j=i;j<maxn;j+=i)
            {
                p[j]=p[j]/i*(i-1);
            }
        }
    }
}

欧拉降幂

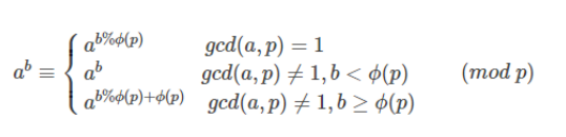
p为质数的话，欧拉函数值即为1.
详见