手写VIO之Bundle Adjustment-优快云博客

深蓝学院《从零开始手写VIO》作业五

1. 完成Bundle Adjustment求解器
2. 完成测试函数
3. 论文总结

1. 完成Bundle Adjustment求解器

完成单目 Bundle Adjustment 求解器 problem.cc 中的部分代码。
• 完成 Problem::MakeHessian() 中信息矩阵 H 的计算。
• 完成 Problem::SolveLinearSystem() 中 SLAM 问题的求解

MakeHessian() 补充代码如下：

// TODO:: home work. 完成 H index 的填写.
H.block(index_i,index_j, dim_i, dim_j).noalias() += hessian;
if (j != i) {
	// 对称的下三角
	// TODO:: home work. 完成 H index 的填写.
	H.block(index_j,index_i, dim_j, dim_i).noalias() += hessian.transpose();

SolveLinearSystem()补充代码如下：

// TODO:: home work. 完成矩阵块取值，Hmm，Hpm，Hmp，bpp，bmm
MatXX Hmm = Hessian_.block(reserve_size,reserve_size, marg_size, marg_size);
MatXX Hmp = Hessian_.block(reserve_size,0, marg_size, reserve_size);
MatXX Hpm = Hessian_.block(0, reserve_size, reserve_size, marg_size);
VecX bpp = b_.segment(0,reserve_size);
VecX bmm = b_.segment(reserve_size,marg_size);

// TODO:: home work. 完成舒尔补 Hpp, bpp 代码
MatXX tempH = Hpm * Hmm_inv;
H_pp_schur_ = Hessian_.block(0,0,reserve_size,reserve_size) - tempH * Hmp;
b_pp_schur_ = bpp - tempH * bmm;

// TODO:: home work. step3: solve landmark
VecX delta_x_ll(marg_size);
delta_x_ll = Hmm_inv*(bmm-Hmp*delta_x_pp);
delta_x_.tail(marg_size) = delta_x_ll;

运行结果如下：

0 order: 0
1 order: 6
2 order: 12

 ordered_landmark_vertices_ size : 20
iter: 0 , chi= 5.35099 , Lambda= 0.00597396
iter: 1 , chi= 0.0289048 , Lambda= 0.00199132
iter: 2 , chi= 0.000109162 , Lambda= 0.000663774
problem solve cost: 22.7924 ms
   makeHessian cost: 19.2487 ms

Compare MonoBA results after opt...
after opt, point 0 : gt 0.220938 ,noise 0.227057 ,opt 0.220992
after opt, point 1 : gt 0.234336 ,noise 0.314411 ,opt 0.234854
after opt, point 2 : gt 0.142336 ,noise 0.129703 ,opt 0.142666
after opt, point 3 : gt 0.214315 ,noise 0.278486 ,opt 0.214502
after opt, point 4 : gt 0.130629 ,noise 0.130064 ,opt 0.130562
after opt, point 5 : gt 0.191377 ,noise 0.167501 ,opt 0.191892
after opt, point 6 : gt 0.166836 ,noise 0.165906 ,opt 0.167247
after opt, point 7 : gt 0.201627 ,noise 0.225581 ,opt 0.202172
after opt, point 8 : gt 0.167953 ,noise 0.155846 ,opt 0.168029
after opt, point 9 : gt 0.21891 ,noise 0.209697 ,opt 0.219314
after opt, point 10 : gt 0.205719 ,noise 0.14315 ,opt 0.205995
after opt, point 11 : gt 0.127916 ,noise 0.122109 ,opt 0.127908
after opt, point 12 : gt 0.167904 ,noise 0.143334 ,opt 0.168228
after opt, point 13 : gt 0.216712 ,noise 0.18526 ,opt 0.216866
after opt, point 14 : gt 0.180009 ,noise 0.184249 ,opt 0.180036
after opt, point 15 : gt 0.226935 ,noise 0.245716 ,opt 0.227491
after opt, point 16 : gt 0.157432 ,noise 0.176529 ,opt 0.157589
after opt, point 17 : gt 0.182452 ,noise 0.14729 ,opt 0.182444
after opt, point 18 : gt 0.155701 ,noise 0.182258 ,opt 0.155769
after opt, point 19 : gt 0.14646 ,noise 0.240649 ,opt 0.14677
------------ pose translation ----------------
translation after opt: 0 :-0.000478009   0.00115904  0.000366508 || gt: 0 0 0
translation after opt: 1 :-1.06959  4.00018 0.863877 || gt:  -1.0718        4 0.866025
translation after opt: 2 :-4.00232  6.92678 0.867244 || gt:       -4   6.9282 0.866025

2. 完成测试函数

完成滑动窗口算法测试函数。
• 完成 Problem::TestMarginalize() 中的代码,并通过测试。

补充代码如下：

// TODO:: home work. 将变量移动到右下角
/// 准备工作： move the marg pose to the Hmm bottown right
// 将 row i 移动矩阵最下面
Eigen::MatrixXd temp_rows = H_marg.block(idx, 0, dim, reserve_size);
Eigen::MatrixXd temp_botRows = H_marg.block(idx + dim, 0, reserve_size - idx - dim, reserve_size);
H_marg.block(idx, 0, dim, reserve_size) = temp_botRows;
H_marg.block(idx + dim, 0, reserve_size - idx - dim, reserve_size) = temp_rows;

// TODO:: home work. 完成舒尔补操作
Eigen::MatrixXd Arm = H_marg.block(0,n2,n2,m2);
Eigen::MatrixXd Amr = H_marg.block(n2,0,m2,n2);
Eigen::MatrixXd Arr = H_marg.block(0,0,n2,n2);

运行结果如下：

---------- TEST Marg: before marg------------
     100     -100        0
    -100  136.111 -11.1111
       0 -11.1111  11.1111
---------- TEST Marg: 将变量移动到右下角------------
     100        0     -100
       0  11.1111 -11.1111
    -100 -11.1111  136.111
---------- TEST Marg: after marg------------
 26.5306 -8.16327
-8.16327  10.2041

3. 论文总结

论文我没有完全看懂，但是我还是结合贺博的讲解尝试将其中提到的对于H矩阵的不同操作方式总一个总结：
论文和课件中由一丢丢不同的是，课件中讨论的是视觉SLAM中的操作方式，而论文中讨论的是VIO中的操作方式，这两者本质不同在于起不可观量不同，视觉SLAM中不可观量由七个，而VIO中只有四个，论文中提到的不同操作方式一共由三种，分别是：
（1）gauge fixation
这种方式的操作是固定第一个相机的位置和yaw轴这四个状态量，在论文中给出的公式为： $\mathbf{p}_{0}=\mathbf{p}_{0}^{0}, \quad \Delta \phi_{0 z} \doteq \mathbf{e}_{z}^{\top} \Delta \phi_{0}=0$ 类比到课件中的操作方式就是：

（2）gauge prior
这种方式的操作是添加先验，增加系统可观性，公式如下： $\left\|\mathbf{r}_{0}^{P}\right\|_{\Sigma_{0}^{P}}^{2}, \quad \text { where } \quad \mathbf{r}_{0}^{P}(\boldsymbol{\theta}) \doteq\left(\mathbf{p}_{0}-\mathbf{p}_{0}^{0}, \Delta \phi_{0 z}\right)$ 类比到课件中的操作方式是：

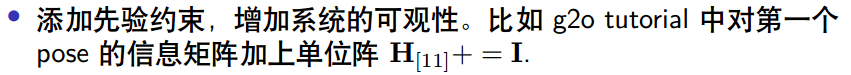
（3）free gauge
这种才操作方式是不对可观性进行操作，但是为了防止奇异矩阵的产生，采用伪逆或者增加一些阻尼项（列文伯格法），因此这种方法实施后可能会对可观性造成影响，也就是会是系统零空间发生变换，对应到课件中操作方式是：

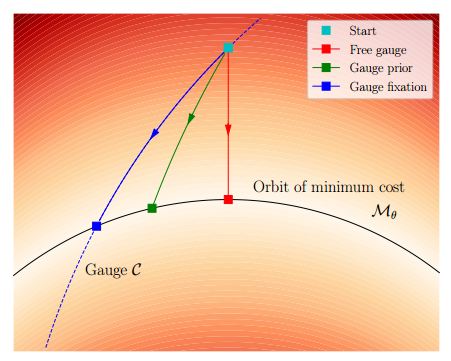
论文中的结论是三种方法的准确性和计算时间是相似的，free gauge的方法会稍微快一些，另外因为free gauge方法会使得零空间发生变化，因此它求解的结果会有很大不同。，下面这幅图说明了三种方法之间的不同，我的个人理解是，黑线

\mathcal{M}_{\theta}

是最小损失值的曲线， 蓝色的线是四个自由度的流形空间的曲线，也是gauge fixation方法代表的曲线，因为gauge fixation中仅仅是固定了第一个状态的位置，因此它的结果会沿着流形空间变换，而 绿色的线是gauge prior方法代表的曲线，因为其增加了先验约束，可以说其损失函数发生了些许变换，因此其最后的状态结果和gauge fixation方法也会由些许不同，而 红色的线是free gauge方法代表的曲线，对于给定的损失函数，free gauge方法使用伪逆选择最小尺寸的参数步骤，因此垂直于成本的等值线移动（最后这一点我不太明白），但是可以看出来其结果与前两者会有很大区别。