基于mxnet的LSTM实现

RNN理论基础

基本RNN结构

rnn_base.png

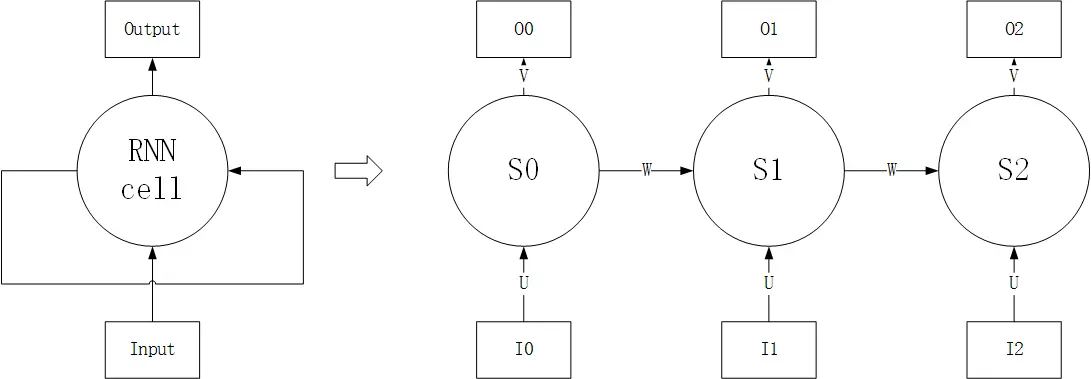
RNN的基本结构如上左图所示，输出除了与当前输入有关，还与上一时刻状态有关。RNN结构展开可视为上右图，传播过程如下所示：

• $I_{n}$为当前状态的输入
• $S_{n}$为当前状态，与当前输入与上一时刻状态有关，即$S_{n} = f(W * S_{n - 1} + U * I_{n})$，其中f(x)为激活函数
• $O_{n}$为当前输出，与状态有关，为$O_{n} = g(V * S_{n})$，其中f(x)为激活函数

整个结构共享参数U,W,V。

当输入很长时，RNN的状态中的包含最早输入的信息会被“遗忘”，因此RNN无法处理非常长的输入

基本LSTM结构

lstm_base.png

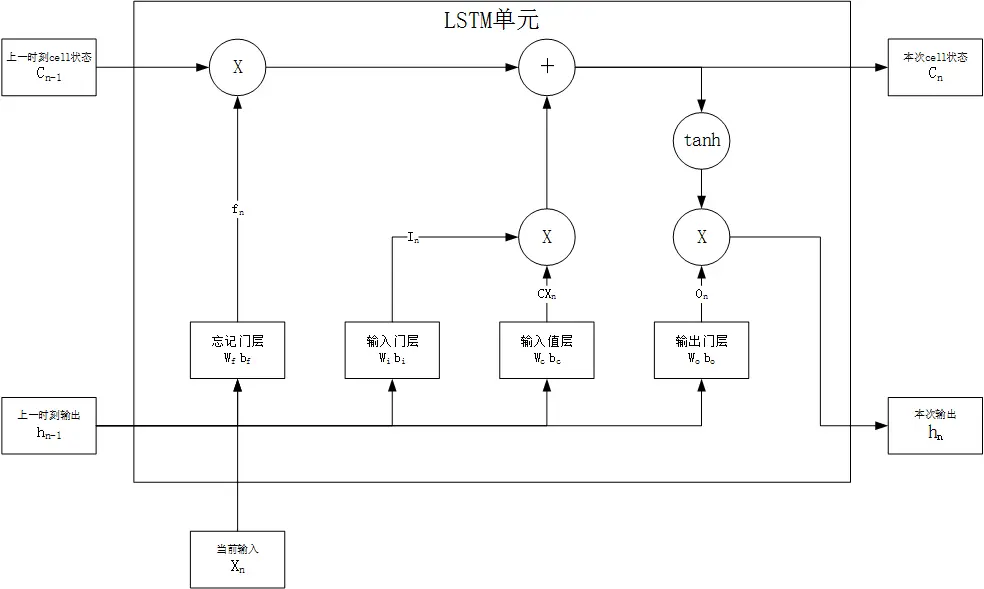
LSTM为特殊为保存长时记忆而设计的RNN单元，传递过程如下：

• 遗忘：决定上一时刻的状态有多少被遗忘，由遗忘门层完成，有$f_{n} = sigmoid(W_{f} * [h_{n-1},x_{n}] + b_{f})$，该结果输出的矩阵与$C_{n-1}$对应位置相乘，对状态起衰减作用
• 输入：决定哪些新信息被整合进状态，由输入值层和输入门层完成：
  • 输入值层决定新输入数据，有$CX_{n} = tanh(W_{c} * [h_{n - 1},x_{n}] + b_{c})$
  • 输入门层决定哪些新数据被整合入状态，有$I_{n} = sigmoid(W_{i} * [h_{n - 1},x_{n}] + b_{i})$
  • 最终汇入状态的输入有$C_{n} = C_{n-1} * f_{n} + I_{n} * CX_{n}$
• 输出：决定哪些状态被输出，由输出门层完成：
  • 输出门层决定哪些状态被输出，有$O_{n} = sigmoid(W_{o} * [h_{n-1},x_{n}] + b_{o})$
  • 最终输入为$h_{n} = O_{n} * tanh(C_{n})$

参数一共有4对，如下表所示

参数功能	参数对
忘记门层，决定哪些状态被遗忘	$W_{f}$,$b_{f}$
输入门层，决定哪些新输入被累积入状态	$W_{c}$,$b_{c}$
输入值层，产生新输入	$W_{i}$,$b_{i}$
输出门层，决定哪些状态被输出	$W_{o}$,$b_{o}$