一、 卡尔曼滤波
卡尔曼滤波的应用要求系统和底层过程的测量模型都是线性的。离散时间线性状态空间系统的描述为:
x
k
=
Φ
k
,
k
−
1
x
k
−
1
+
G
k
−
1
w
k
−
1
x_k=\Phi_{k,k-1}x_{k-1}+G_{k-1}w_{k-1}
xk=Φk,k−1xk−1+Gk−1wk−1
式中
Φ
k
,
k
−
1
\Phi_{k,k-1}
Φk,k−1为状态转移矩阵,
x
k
x_k
xk为状态向量,
G
k
−
1
G_{k-1}
Gk−1为噪声分布矩阵,
w
k
−
1
w_{k-1}
wk−1为过程噪声向量,k为测量历元。
系统的测量方程由下式给出
z
k
=
H
k
x
k
+
η
k
z_k=H_kx_k+\eta_k
zk=Hkxk+ηk
式中
z
k
z_k
zk为系统输出的测量向量,
H
k
H_k
Hk为观测或设计,
η
k
\eta_k
ηk为测量噪声。系统噪声w和测量噪声
η
k
\eta_k
ηk是具有确定的自协方差函数的非相关零均值白噪声过程。
通过对钻柱动力学的分析,提出了一种新的状态空间模型算法。在计算方法中,我们定义KF-1的输入矢量为
X
=
[
a
x
a
y
a
z
m
x
m
y
m
z
]
X=\begin{bmatrix}a_x&a_y&a_z\\ m_x&m_y&m_z\end{bmatrix}
X=[axmxaymyazmz],由三轴磁强计和三轴加速度计测量。KF-2的输入向量为井眼倾角和方位角,定义为
X
=
[
I
A
]
X=\begin{bmatrix}I\\ A\end{bmatrix}
X=[IA],其中
I
I
I为井眼倾角,
A
A
A为井眼方位角。
求解过程如下图所示:

在此过程中,设计两个卡尔曼滤波器。在KF-1之后,我们可以得到更精确的重力加速度信号gx, gy和gz,定义为KF-1的输出。利用重力加速度,通过建立钻柱旋转时的方程,可以得到钻柱的倾角和方位角。然后使用KF-2进一步平滑钻井轨迹。KF-2的输出定义为
M
′
=
[
I
′
A
′
]
T
M'=\begin{bmatrix}I'&A'\end{bmatrix}^T
M′=[I′A′]T,这是更精确的。
1.1 KF-1的状态空间模型
传感器安装在钻柱的中心,在旋转过程中,x轴和y轴的测量信号呈现正弦波。理论上,加速度计和磁力计的信号有相同的规律。在实际钻井过程中,钻柱的振动对磁强计信号的影响较小。也就是说,磁力计信号是用来校准加速度计信号的。通过实验室测试,我们可以得出磁通门信号的变化与重力加速度信号的变化是一致的。
假设角速度为
w
x
,
y
,
z
w_{x,y,z}
wx,y,z,采样间隔为Δt,则
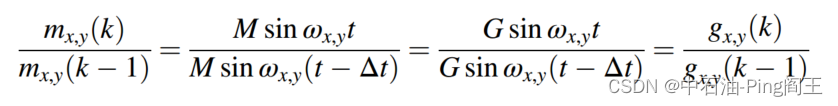
在KF-1中,我们将状态向量定义为
X
=
[
g
x
(
k
)
g
y
(
k
)
g
z
(
k
)
]
X=\begin{bmatrix}g_x{(k)}\\g_y{(k)}\\g_z{(k)}\end{bmatrix}
X=
gx(k)gy(k)gz(k)
,从
a
x
,
a
y
,
a
z
a_x,a_y,a_z
ax,ay,az的振动信号可以得到重力加速度信号
x
g
(
k
)
x_g{(k)}
xg(k)。因此,系统输出的测量矢量为,当钻柱旋转时,除了z轴信号外,x轴和y轴的测量信号将呈现正弦波。因此,变换矩阵定义为
z
(
k
)
=
[
a
x
a
y
a
z
]
z(k)=\begin{bmatrix}a_x\\a_y\\a_z\end{bmatrix}
z(k)=
axayaz
,
H
k
=
[
m
x
(
k
−
1
)
m
x
(
k
)
0
0
0
m
y
(
k
−
1
)
m
y
(
k
)
0
0
0
1
]
H_k=\begin{bmatrix}\frac{m_x{(k-1)}}{m_x{(k)}}&0&0\\ 0&\frac{m_y{(k-1)}}{m_y{(k)}}&0\\ 0&0&1\end{bmatrix}
Hk=
mx(k)mx(k−1)000my(k)my(k−1)0001
。系统噪声
w
k
w_k
wk和测量噪声
η
k
\eta_k
ηk是不相关的零均值白噪声过程。因此,我们得到KF-1的状态空间模型如下:
x
g
(
k
)
=
[
m
x
(
k
−
1
)
m
x
(
k
)
0
0
0
m
y
(
k
−
1
)
m
y
(
k
)
0
0
0
1
]
x
g
(
k
−
1
)
+
[
w
x
(
k
−
1
)
w
y
(
k
−
1
)
w
z
(
k
−
1
)
]
x_g{(k)}=\begin{bmatrix}\frac{m_x{(k-1)}}{m_x{(k)}}&0&0\\ 0&\frac{m_y{(k-1)}}{m_y{(k)}}&0\\ 0&0&1\end{bmatrix}x_g{(k-1)+\begin{bmatrix}w_x{(k-1)}\\w_y{(k-1)}\\w_z{(k-1)}\end{bmatrix}}
xg(k)=
mx(k)mx(k−1)000my(k)my(k−1)0001
xg(k−1)+
wx(k−1)wy(k−1)wz(k−1)
z
(
k
)
=
H
k
x
g
(
k
)
+
η
(
k
)
z(k)=H_kx_g{(k)}+\eta(k)
z(k)=Hkxg(k)+η(k)
1.2 计算倾角和方位角
钻柱旋转时,上述方程不适用。安装在钻柱中心的传感器,即x轴和y轴的测量信号,在旋转过程中呈现正弦波。
通过KF-1,我们得到gx、gy和gz,它们分别定义为x、y和z轴上的重力加速度测量信号。然后定义系统的输入向量为
X
′
=
[
g
x
g
y
g
z
m
x
m
y
m
z
]
X'=\begin{bmatrix}g_x&g_y&g_z\\ m_x&m_y&m_z\end{bmatrix}
X′=[gxmxgymygzmz]。
定义转速为R,若R为0,则用下式计算倾角和方位角。
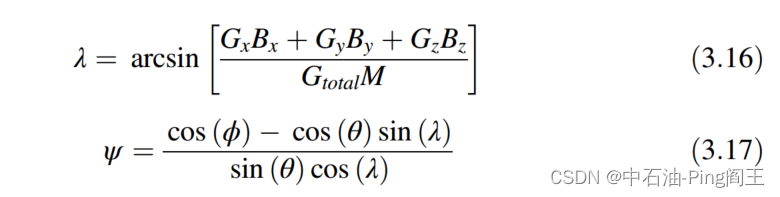
R
≠
0
R\neq0
R=0表示钻柱在旋转,倾角I和方位角A的计算公式如下:
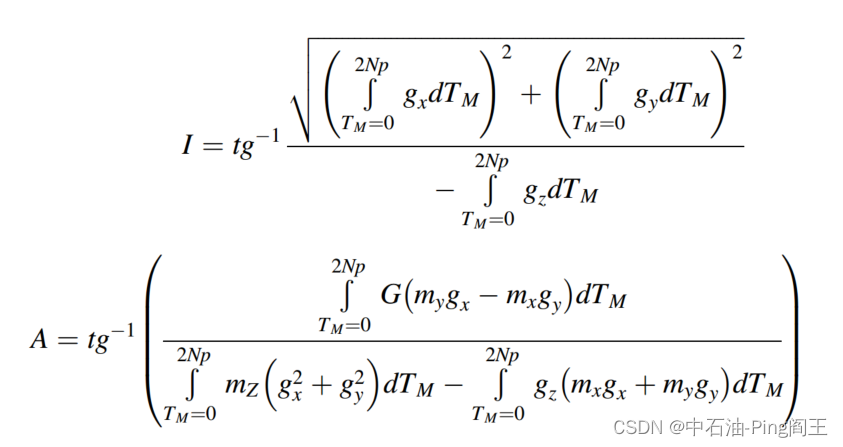
式中
T
M
T_M
TM为磁性工具面角:
T
M
=
t
g
−
1
(
−
m
y
m
x
)
T_M=tg^-1(\frac{-m_y}{m_x})
TM=tg−1(mx−my)。用于近直井的工具面角。磁性工具面是在垂直于井筒轴线的平面上,顺时针方向测量的井眼测量仪器在井筒内的角度或方位角;北、东、南、西方向的磁性工具面角分别为0°、90°、180°和270°。磁性工具面可以校正为参考栅格北或真北。
虽然钻柱转速是判断钻柱是否旋转的一种方法,但这种方法的可靠性不高。相反,使用标准差统计方法来确定钻柱的运动更加可靠,因为它反映了群体中个体之间的分散程度。使用50个数据点作为时间窗口,假设它们是x1, x2,…, x49, x50,我们得到标准差
σ
=
1
N
∑
i
=
1
N
(
x
i
−
x
ˉ
)
2
\sigma=\sqrt{\frac{1}{N}\sum_{i=1}^N(x_i-\bar{x})^2}
σ=N1∑i=1N(xi−xˉ)2,当标准差σ接近于零时,钻柱可以认为是静止的。
1.3 KF-2的状态空间模型
在钻孔过程中,运动状态为
σ
=
0
\sigma=0
σ=0和
σ
≠
0
\sigma\neq0
σ=0交替出现。当
σ
≠
0
\sigma\neq0
σ=0时,由于钻柱不旋转时振动较小,求解结果更为准确。我们开发了另一种卡尔曼滤波器(KF-2)来平滑钻井轨迹。(KF-2分别分为KF-2.1和KF2.2,如下图所示。)
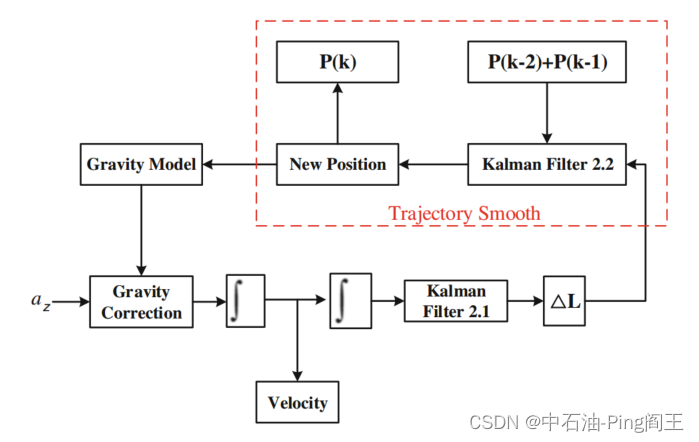
在正常的钻井过程中,为了测量倾角和方位角,钻井作业经常要停在测量站。然后根据数学假设计算两个测量站之间的井眼轨迹。例如,可以假设钻孔距离为直线、圆弧或多角线;每个都需要不同的计算方法。设实际钻井轨迹测量第N点的三维坐标为
(
x
N
,
y
N
,
z
N
)
(x_N,y_N,z_N)
(xN,yN,zN),则测量(N +1)点为
(
x
N
+
1
,
y
N
+
1
,
z
N
+
1
)
(x_{N+1},y_{N+1},z_{N+1})
(xN+1,yN+1,zN+1),井深、垂深、倾角、方位角分别为
L
N
、
H
N
、
θ
N
、
Ψ
N
L_N、H_N、\theta_N、\Psi_N
LN、HN、θN、ΨN和$L_{N+1}、H_{N+1}、\theta_{N+1}、\Psi_{N+1}。两点之间的井眼轨迹定义如下:

如果垂直深度H已知,则测量(N + 1)-th点的三维坐标可定义为
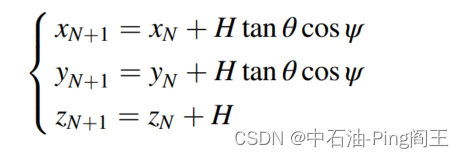
我们可以通过递归计算得到每个点的空间坐标,从而得到整个钻井轨迹。如下图所示,我们可以使用井眼轨迹外推法建立相邻两个测点之间的递推关系。
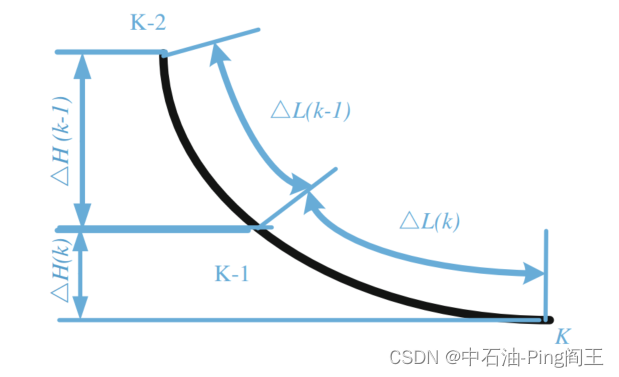
假设L是钻孔深度,
γ
\gamma
γ是钻孔轨迹与其切线的夹角,然后:
L
(
k
)
=
L
(
k
−
1
)
+
Δ
L
(
K
)
L(k)=L(k-1)+\Delta L(K)
L(k)=L(k−1)+ΔL(K)
γ
=
a
r
c
c
o
s
[
c
o
s
(
I
k
−
2
)
c
o
s
(
I
k
−
1
)
+
s
i
n
(
I
k
−
2
)
s
i
n
(
I
k
−
1
)
c
o
s
(
A
k
−
1
−
A
k
−
2
)
]
\gamma=arccos[cos(I_{k-2})cos(I_{k-1})+sin(I_{k-2})sin(I_{k-1})cos(A_{k-1}-A_{k-2})]
γ=arccos[cos(Ik−2)cos(Ik−1)+sin(Ik−2)sin(Ik−1)cos(Ak−1−Ak−2)]
γ
(
k
)
=
γ
Δ
L
(
k
−
1
)
Δ
L
(
k
)
\gamma(k)=\frac{\gamma}{\Delta L(k-1)}\Delta L(k)
γ(k)=ΔL(k−1)γΔL(k)
从上面三个公式看出,我们可以使用两个点来估计下一个点,因此可以平滑井眼轨迹。我们可以使用Kalman Filter 2.2对钻井轨迹进行校准,其中将第k个测量点定义为
P
(
k
)
=
[
I
k
A
k
]
P(k)=[I_k A_k]
P(k)=[IkAk]。系统输入为P(K -2)和P(K -1), KF-2.2结合实测值和理论计算值估算P(K)。
KF-2.2通过倾角和方位角作为输入,实现井眼轨迹平滑。假设状态向量为
x
(
k
)
=
[
I
k
A
k
]
x(k)=\begin{bmatrix}I_k\\A_k\end{bmatrix}
x(k)=[IkAk],则系统输出的测量向量为
x
(
k
)
=
[
I
k
A
k
]
m
x(k)=\begin{bmatrix}I_k\\A_k\end{bmatrix}_m
x(k)=[IkAk]m,
H
(
k
)
=
[
1
0
0
1
]
H(k)=\begin{bmatrix}1&0\\0&1\end{bmatrix}
H(k)=[1001]。得到KF-2.2的状态空间模型:
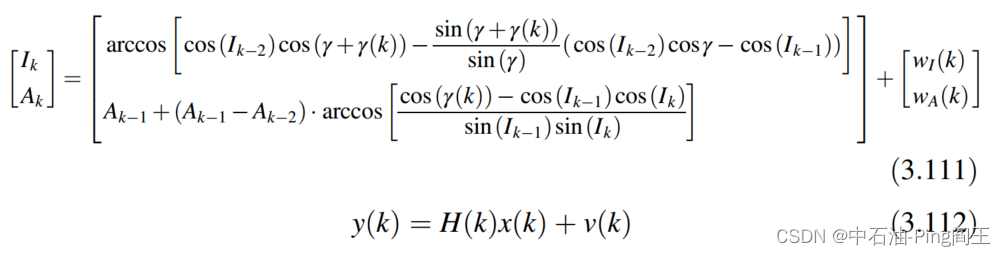
如上所示,我们应该确定
Δ
L
\Delta L
ΔL作为KF-2.2的输入。(
Δ
t
\Delta t
Δt期间钻头向前移动的距离)。我们可以通过测量z轴上的加速度来计算位移。
A
z
A_z
Az是z轴上三轴加速度计的信号,它与重力加速度和振动加速度相结合。定义加速度在z轴时间序列上的测量为
a
z
(
k
)
a_z(k)
az(k)。
所以在计算位移
Δ
L
\Delta L
ΔL之前,我们首先要排除重力的影响,如下所示:
f
g
z
(
k
)
=
a
z
(
k
)
−
G
⋅
c
o
s
(
I
k
−
1
)
f_{g_z}(k)=a_z(k)-G·cos(I_{k-1})
fgz(k)=az(k)−G⋅cos(Ik−1)
其中
f
g
z
(
k
)
f_{g_z}(k)
fgz(k)是加速度时间序列函数,通过去掉
g
z
g_z
gz的加速度,可以计算出
a
z
(
k
)
a_z(k)
az(k)和倾角
I
k
−
1
I_{k-1}
Ik−1对应的同一时间。
然后我们可以使用z轴时间序列
f
g
z
(
k
)
f_{g_z}(k)
fgz(k)上的加速度来计算钻探深度(
Δ
L
\Delta L
ΔL)。将状态向量定义为
Δ
L
(
k
)
=
[
Δ
L
(
k
)
Δ
L
˙
(
k
)
Δ
L
¨
(
k
)
]
\Delta L(k)=\begin{bmatrix}\Delta L(k)\\\Delta \dot L(k)\\\Delta \ddot L(k)\end{bmatrix}
ΔL(k)=
ΔL(k)ΔL˙(k)ΔL¨(k)
,系统输出的测量向量为
z
(
k
)
=
f
g
z
(
k
)
z(k)=f_{g_z}(k)
z(k)=fgz(k),我们建立了KF-2.1的状态空间模型如下:
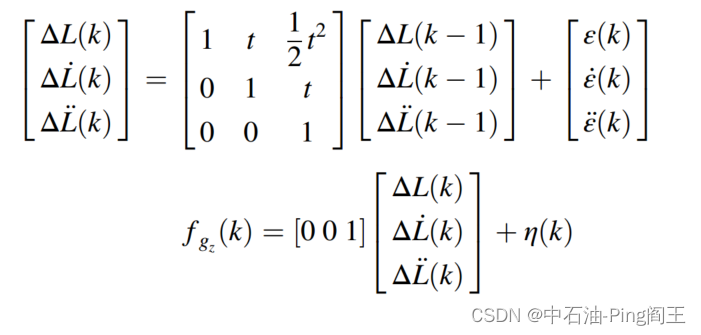
通过对实测信号进行预处理,建立了一种基于底部旋转钻具动力学分析的动态方位和倾角求解算法。在理论模型的基础上,我们开发了一种卡尔曼滤波器来提高求解器的精度;在预测钻井轨迹的基础上,建立了卡尔曼滤波的状态空间方程。基于卡尔曼滤波的动态测量算法是一种能够大大降低求解误差的新模型。
二、 往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法





 文章详细介绍了卡尔曼滤波在钻柱动力学中的应用,包括KF-1和KF-2两种滤波器的设计,用于处理加速度计和磁强计数据,计算重力加速度并平滑井眼轨迹。文中涉及状态空间模型、测量噪声处理和动态角度计算方法。
文章详细介绍了卡尔曼滤波在钻柱动力学中的应用,包括KF-1和KF-2两种滤波器的设计,用于处理加速度计和磁强计数据,计算重力加速度并平滑井眼轨迹。文中涉及状态空间模型、测量噪声处理和动态角度计算方法。


















 1862
1862

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










