PCL点云处理之分层切片法计算树冠投影面积 （一百七十四）

已于 2023-06-03 22:46:01 修改
阅读量2k 收藏 7
点赞数 1
CC 4.0 BY-SA版权
分类专栏： 点云算法合集 PCL点云处理学习 文章标签： 分层投影 切片法 树冠投影面积 几何学 PCL算法
于 2023-06-03 11:26:28 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_44329757/article/details/131019136
本文介绍了使用PCL库通过分层切片法来精确计算树冠投影面积的方法。首先，概述了算法原理，然后详细说明了包括设置切片层数、计算层高等步骤，接着展示了代码实现和实验效果。最后，对算法使用时的注意事项进行了总结，强调了点云层数不宜过多以及投影面积计算可采用二维凸包算法。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

PCL点云处理之分层切片法计算树冠投影面积 （一百七十四）

一、算法介绍

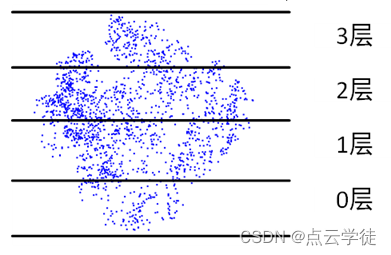
在这里插入图片描述

在上一节中，通过树冠整体投影到同一水平面后，计算凸包面积，粗略估计了树冠投影面积，但在通常的研究学习中，这种方法较为笼统，大部分的树冠投影面积计算是通过将整个树冠分层切片后，逐一计算比较切片点云面积，将最大面积作为树冠投影面积，这一计算结果相对更合理准确，但其计算过程稍微复杂一些，这里对此进行实现，具体的实现方法和代码，以及效果如下所示意：

二、方法流程

1、人工选择切片层数，预设置点云容器
2、计算点云高程最值，最大与最小
3、根据高差和切片数量，计算层高
4、遍历点云，依次确定每个点的所在层数，放入对应容器
5、使用二维凸包面积计算，对每层点云进行面积计算
6、比较确定最大面积，作为最终的投影面积

三、具体实验

1.代码

#include <pcl/io/
了解本专栏 订阅专栏 解锁全文
PCL 点云切片
点云侠的博客
11-10 6064
点云切片的C++代码实现
PCL：实现点云切片（附完整源码）
希望我的博客，能帮上你解决学习中工作中所遇到的问题
10-13 466
PCL：实现点云切片（附完整源码）
PCL点云切片：从基础算法到实际应用
QsPascal的博客
09-26 691
其中最常用的滤波器是体素滤波器（VoxelGrid），它将点云数据划分为小立方体（体素），并取每个体素内的一个点作为该体素的代表。在处理点云数据时，点云切片是一种重要的算法，它可以将点云数据按照特定的切片方式进行分割和处理。本文将介绍PCL（点云库）中点云切片的基础算法，并通过源代码实现一个简单的点云切片应用。总结起来，PCL点云库提供了丰富的滤波器和算法，能够实现灵活高效的点云切片。当然，PCL还提供了其他各种滤波器和算法，可以根据具体需求进行选择和组合，并实现更复杂的点云切片应用。
点云切片；点云平面切割
11-23
主要用于三维点云的平板分割, 每次只能分割出一个平面。 (It is mainly used for 3D point cloud segmentation.Only one plane can be segmented at a time.)
PCL 点云沿任意指定方向进行等距切片（C++详细过程版）
点云侠的博客
05-16 1723
从点云中选取两个点，构成指定的切片方向，沿着给定方向对点云进行等间距切片。
PCL点云处理之单木树冠投影面积粗略估计（一百七十三）
weixin_44329757的博客
06-02 603
树冠投影面积、体积、树高、胸径、等森林单木因子的精确测量是林业从业者进行生长监测的必要手段，这些因子的测量最好满足操作简单、自动化、精度高、不破坏林木本身生长等要求。激光雷达可以快速扫描树木的点云，不必接触到树木，后续通过算法可以快速实现相关因子的计算。最近那个最高树不就是激光扫描得到的吗哈哈。
PCL点云处理之凸包法提取树冠体积 （一百七十六）
weixin_44329757的博客
06-03 672
凸包法直接计算树冠体积，对于部分冠点分布均匀充盈的树种是非常快速准确计算体积的方法，下面是具体实现和效果测试。后面会逐步实现其他的不规则点云体积计算方法，用于树冠体积或者其他体积的计算应用。
PCL点云处理之全字段重心计算 （一百七十八）
weixin_44329757的博客
06-04 489
点云属性除了三维坐标外，还包括颜色，强度等多种属性，在后续计算中不可或缺，PCL库提供了专门的点云重心计算方法，可以对点云的全部属性进行重心计算，而不是只对坐标计算重心，具体的计算代码和结果如下所示： 2.效果
树冠点云投影面积计算（凸包法）
dayuhaitang1的博客
02-08 4848
树冠投影面积计算
基于PCL的点云切片算法
QsPascal的博客
09-25 531
通过创建条件滤波器和调用滤波器对象的filter函数，我们可以对点云数据进行切片操作，并得到切片后的点云数据。点云切片是一种常用的点云处理技术，它可以将点云数据按照特定的切片方式进行分割和提取，从而实现对点云数据的进一步分析和处理。在主函数中，我们首先读取一个点云文件，然后调用切片函数进行点云切片操作，并将切片后的点云数据保存到另一个文件。通过调用切片函数，我们可以将输入点云数据按照指定的切片阈值进行切片，并得到切片后的点云数据。该函数接受一个输入点云和一个切片阈值作为参数，并返回切片后的点云数据。
点云切片C++代码 求取点云体积的上一步
01-23
点云切片C++代码 求取点云体积的上一步
基于PCL、VTK的切片法计算三维模型的体积
07-22
采用C++ 切片法计算封闭三维模型（三角形网格模型）的体积。计算速度快，计算准确。
点云切片的C++代码实现.rar
09-03
基于PCL使用C++代码实现的点云切片，包含代码，算法原理和实验数据。基于PCL使用C++代码实现的点云切片，包含代码，算法原理和实验数据。基于PCL使用C++代码实现的点云切片，包含代码，算法原理和实验数据。基于PCL使用C++代码实现的点云切片，包含代码，算法原理和实验数据。
PCL 点云沿坐标轴进行等距切片【2024最新版】
点云侠的博客
08-11 3235
沿坐标轴方向对点云数据进行等距离切片的PCL普通代码以及多线程并行加速代码实现。博客长期更新，本文最近更新时间为：2024年11月20日。
PCL点云切片算法程序
qq_39897387的博客
02-22 2346
#include <pcl/ModelCoefficients.h> #include <pcl/io/pcd_io.h> #include <pcl/io/pcd_io.h> #include <pcl/point_types.h> #include <pcl/filters/extract_indices.h> #include <pcl/filters/passthrough.h> #include <pcl/featur.
PCL 切片法实现点云模型的体积测量、面积测量（二）
weixin_43896283的博客
01-05 1483
通过PCL VTK进行切片法，实现点云模型的体积测量、面积测量。
CloudCompare&PCL 点云等间距切片
dayuhaitang1的博客
07-14 1934
CloudCompare&PCL 点云等间距切片
PCL提供的几种点云分割的方法
热门推荐
AmbitiousRuralDog的博客
05-11 1万+
前言： 点云识别的深度学习极其需要噪声少的物体点云来作为训练集。获得噪声少的物体点云需要一个好的点云分割器。PCL官方网站:http://pointclouds.org/documentation/tutorials/#segmentation-tutorial提供10来种点云分割的方法，让我来聊聊我的浅见。 PCL提供的点云分割的方法： 1. Plane model segmenta...
PCL点云处理之基于最小割的点云分割（九十六）
weixin_44329757的博客
01-30 1092
点云分割方法之最小割PCL
pcl点云处理之手写
最新发布
03-15
### 手写实现 PCL 点云处理 #### 主成分分析 (PCA) 计算点云最小包围盒 为了计算点云的最小包围盒，可以利用主成分分析（Principal Component Analysis, PCA），这种方法适用于小场景物体（如人、树、车辆等）并具有较高的效率。以下是具体实现过程： 1. **加载点云数据** 需要先读取或生成目标点云数据。 2. **中心化点云** 将点云中的所有点平移到原点附近，以便后续计算更加稳定。 3. **构建协方差矩阵** 使用点云坐标构建协方差矩阵，并对其进行特征分解以获得主方向。 4. **旋转点云至标准姿态** 利用主方向对齐点云到新的坐标系下。 5. **计算边界框尺寸** 在新坐标系中找到最大和最小值作为包围盒的边长。 ```cpp #include <iostream> #include <Eigen/Dense> // Eigen库用于线性代数运算 #include <pcl/point_cloud.h> #include <pcl/point_types.h> void computeBoundingBox(const pcl::PointCloud<pcl::PointXYZ>::Ptr& cloud) { // 中心化点云 Eigen::Vector4f centroid; pcl::compute3DCentroid(*cloud, centroid); for(auto& point : cloud->points){ point.x -= centroid[0]; point.y -= centroid[1]; point.z -= centroid[2]; } // 构建协方差矩阵 Eigen::Matrix3f covariance_matrix = Eigen::Matrix3f::Zero(); pcl::computeCovarianceMatrixNormalized(*cloud, centroid, covariance_matrix); // 特征分解得到主方向 Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> eigen_solver(covariance_matrix); Eigen::Matrix3f eigenvectors = eigen_solver.eigenvectors(); // 创建变换矩阵 Eigen::Matrix4f rotation = Eigen::Matrix4f::Identity(); rotation.block<3, 3>(0, 0) = eigenvectors.transpose(); // 应用变换 pcl::PointCloud<pcl::PointXYZ>::Ptr rotated_cloud(new pcl::PointCloud<pcl::PointXYZ>()); pcl::transformPointCloud(*cloud, *rotated_cloud, rotation); // 寻找包围盒大小 float min_x = std::numeric_limits<float>::max(), max_x = -std::numeric_limits<float>::max(); float min_y = std::numeric_limits<float>::max(), max_y = -std::numeric_limits<float>::max(); float min_z = std::numeric_limits<float>::max(), max_z = -std::numeric_limits<float>::max(); for(auto const &pt : rotated_cloud->points){ if(pt.x < min_x){min_x= pt.x;} if(pt.x > max_x){max_x= pt.x;} if(pt.y < min_y){min_y= pt.y;} if(pt.y > max_y){max_y= pt.y;} if(pt.z < min_z){min_z= pt.z;} if(pt.z > max_z){max_z= pt.z;} } } int main(){ pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>()); // 假设此处已填充点云数据... computeBoundingBox(cloud); } ``` 上述代码实现了基于 PCA 的点云最小包围盒计算[^1]。 --- #### 直通滤波器的应用 对于去除不需要的部分点云区域，可以通过直通滤波器完成这一操作。以下是一个简单的 C++ 实现示例： ```cpp #include <pcl/filters/passthrough.h> void passThroughFilter(pcl::PointCloud<pcl::PointXYZ>::Ptr inputCloud, pcl::PointCloud<pcl::PointXYZ>::Ptr outputCloud, const std::string& filterField, double lowerLimit, double upperLimit) { pcl::PassThrough<pcl::PointXYZ> pass; pass.setInputCloud(inputCloud); // 设置输入点云 pass.setFilterFieldName(filterField.c_str()); // 设置过滤字段名（X,Y,Z） pass.setFilterLimits(lowerLimit, upperLimit);// 设定上下限 pass.filter(*outputCloud); // 输出结果 } int main() { pcl::PointCloud<pcl::PointXYZ>::Ptr inputCloud(new pcl::PointCloud<pcl::PointXYZ>()); pcl::PointCloud<pcl::PointXYZ>::Ptr filteredCloud(new pcl::PointCloud<pcl::PointXYZ>()); // 调用函数执行滤波 passThroughFilter(inputCloud, filteredCloud, "z", 0.0, 1.0); return 0; } ``` 这段代码展示了如何使用 `pcl::PassThrough` 类来移除指定范围内不符合条件的点云部分[^2]。 --- #### 圆锥形点云生成 如果需要生成特定形状的点云（例如圆锥体），则可以根据几何关系手动定义其顶点分布。下面提供了一个生成圆锥面点云的例子： ```cpp #include <cmath> #include <vector> #include <pcl/point_cloud.h> #include <pcl/point_types.h> pcl::PointCloud<pcl::PointXYZ>::Ptr generateCone(float baseRadius, float height, int resolution) { pcl::PointCloud<pcl::PointXYZ>::Ptr coneCloud(new pcl::PointCloud<pcl::PointXYZ>()); for(int i = 0; i <=resolution;i++){ float h = static_cast<float>(i)/resolution*height; // 当前高度比例 float r = baseRadius*(1-h/height); // 半径随高度变化 for(int j =0 ;j<=resolution;j++) { // 绘制一圈上的点 float theta = 2*M_PI/static_cast<float>(resolution)*j;// 角度 pcl::PointXYZ p(r*cos(theta),r*sin(theta),h); // 定义三维空间位置 coneCloud->push_back(p); } } return coneCloud; } int main(){ auto cone = generateCone(1.0, 2.0, 100); } ``` 以上程序能够按照给定分辨率生成一个近似圆锥结构的点云集[^3]。 ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

点云学徒

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值