1. 电磁波
电磁波,即空间中移动的磁场和电场,是电磁学中的基本现象之一。在真空中,电磁波移动速度为光速,且运动轨迹通常为直线
我们可以将电磁波解析为磁场分量和电场分量,示意图如下:
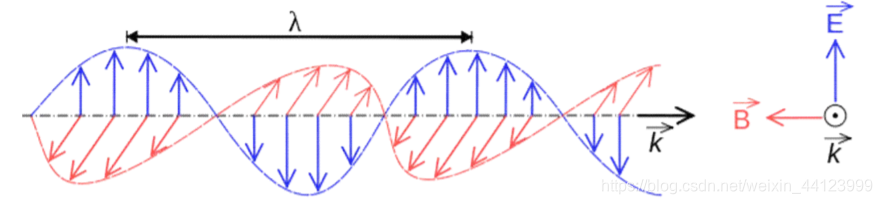
电磁波的特性有两个,频率(frequency)和波长(wavelength),可能的频率范围被称为频谱(spectrum),真空中波长λ\lambdaλ和频率fff的关系如下
λ=c0f\lambda=\frac{c_0}{f}λ=fc0
其中c0c_0c0是光速,c0=3×108m/sc_0=3\times10^8m/sc0=3×108m/s
2. 波动方程
假设有一个均匀的无源介质,它的介电常数为ε\varepsilonε,磁导率为μ\muμ,电导率为σ\sigmaσ,则根据麦克斯韦方程组,可以得出
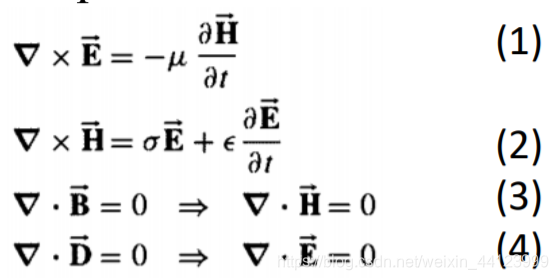
上面方程的变量为E和H,现在,我们尝试推导出只含有一个变量E的方程
推导的过程这里不会详细介绍,但我们需要记住推导中做出的一些假设
2.1 假设1
波传递的介质是无源介质
ρ=0\rho=0ρ=0
2.2 假设2
我们假设波传递的介质是一个理想的无损介质,这种介质的电导率为0,即
σ=0\sigma=0σ=0
这意味着波在传播的过程中不会出现衰减
2.3 假设3
对于一个平面波,电场分量EEE和磁场分量HHH都处于横截面上,横截面与波传递的方向垂直,鉴于两个分量在纵向z,即波传递的方向上都没有分量,我们可以知道
Ez=0E_z=0Ez=0
Hz=0H_z=0Hz=0
这种波也被称为横向电磁波(tranverse electromagnetic wave),简写为TEM波
2.4 假设4
假设波在一个均匀平面上传播,对于均匀平面波(uniform plane wave),电场分量和磁场分量的值只与z有关,与x,y无关,即E和H的表达式包含z,不包含x,y,因此可以得出

2.5 假设5
电磁波是谐波,关于时间的微分可以用相位表示
2. 6 结果
最终得到只包含E的表达式为
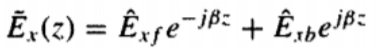
其中ExfE_{xf}Exf是波向前移动时的表达式,ExbE_{xb}Exb是波向后移动时的表达式
2.7 参数计算
2.7.1 波的传播速度
up=ωβ=c0μrϵru_p=\frac{\omega}{\beta}=\frac{c_0}{\sqrt{\mu_r\epsilon_r}}up=βω=μrϵrc0
其中c0c_0c0是光速
2.7.2 波长
λ=upf\lambda=\frac{u_p}{f}λ=fup
2.7.3 固有阻抗
η=η0μrϵr\eta=\eta_0\sqrt\frac{\mu_r}{\epsilon_r}η=η0ϵrμr
其中η0\eta_0η0是真空固有阻抗
























 1822
1822

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








