李萨如图(Lissajous figure)详解与 MATLAB 可视化示例
摘要:李萨如图是由两个互相垂直方向上的简谐运动合成而成的平面轨迹,既有优美的几何形状,又能直接反映两个正弦信号的频率比与相位差。因此它在物理(示波器相位/频率测量)、信号处理与数学视觉化中都很常用。下面先从数学定义、几何性质与仪器学意义讲起,再给出若干 MATLAB 可视化与相位估计的实用代码示例,便于实验与教学使用。
1. 什么是李萨如图(定义)
给定两个互相垂直的简单正弦振动
{x(t)=Asin(at+δ),y(t)=Bsin(bt), \begin{cases} x(t)=A\sin(a t+\delta),\\[4pt] y(t)=B\sin(b t), \end{cases} {x(t)=Asin(at+δ),y(t)=Bsin(bt),
其中 A,BA,BA,B 为振幅,a,ba,ba,b 为角频率(或简记为频率比),δ\deltaδ 为相位差。随着参数 ttt 变化,(x(t),y(t))(x(t),y(t))(x(t),y(t)) 在平面上描出的轨迹即为李萨如图。
李萨如图是指两个沿着垂直方向的正弦信号合成的轨迹,由于其能同时反映两垂直信号的幅值和相位差,常用于信号处理领域。
2. 几何与代数性质(重要结论)
-
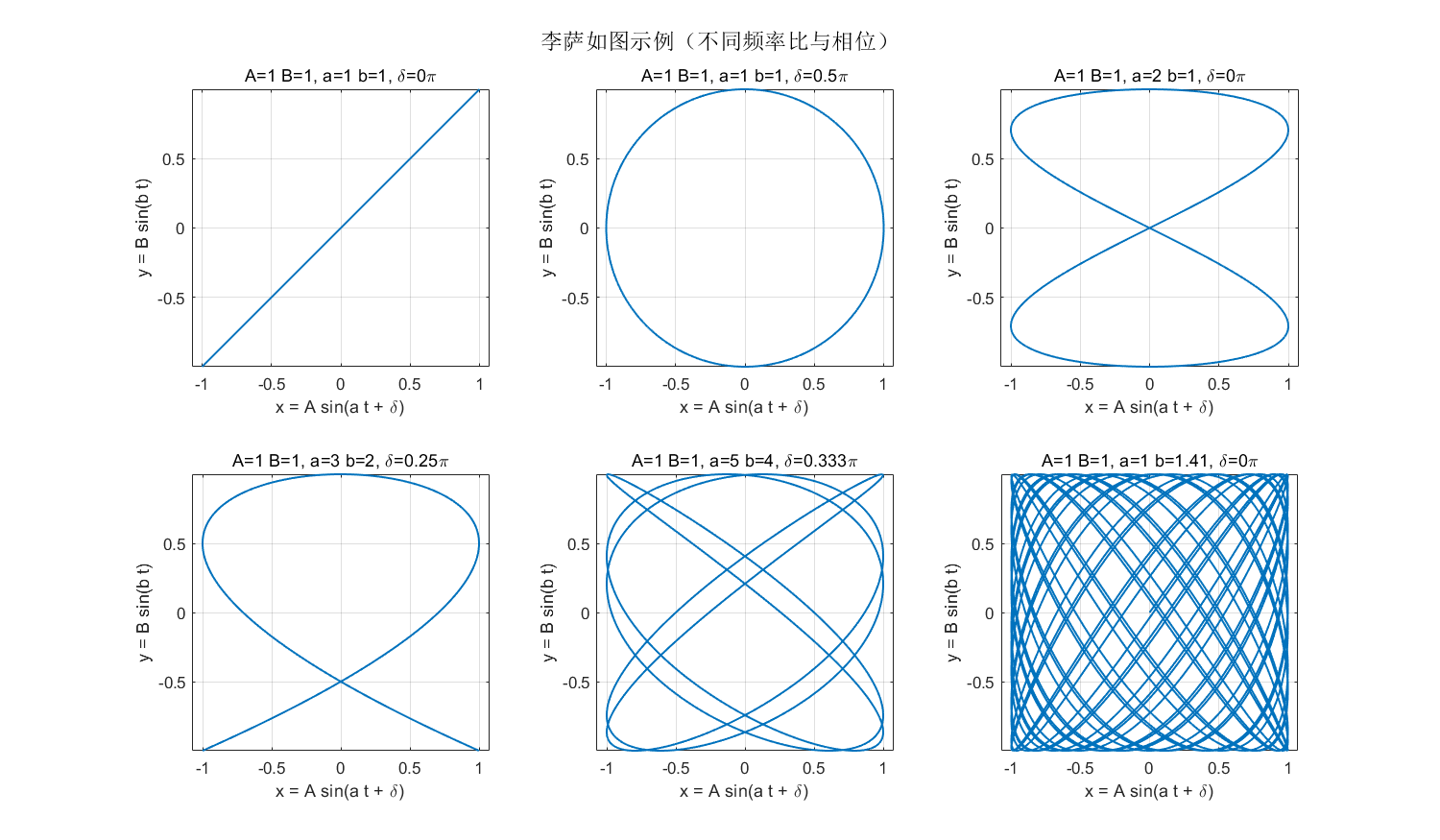
相等频率(a=ba=ba=b):轨迹为椭圆(包括退化为直线或圆的特例)。特别地,当 A=BA=BA=B 且 δ=π2\delta=\tfrac{\pi}{2}δ=2π 时为圆;当 δ=0\delta=0δ=0 时为通过原点的直线 y=(B/A)xy=(B/A)xy=(B/A)x。
可以从三角恒等式消去 ttt 得到常见的椭圆方程(设 s=sin(at)s=\sin(at)s=sin(at)):
x2A2+y2B2−2xycosδAB=sin2δ, \frac{x^2}{A^2}+\frac{y^2}{B^2}-\frac{2xy\cos\delta}{AB}=\sin^2\delta, A2x2+B2y2−AB2xycosδ=sin2δ,
它是一般的二次曲线,δ\deltaδ 控制椭圆的倾角与长短轴比。
-
频率比为有理数(闭合性):若 ab\frac{a}{b}ba 为有理数,设在最简形式为 m:nm:nm:n(互素整数),则轨迹是闭合曲线,会重复。
若 aaa 和 bbb 都是整数,记 g=gcd(a,b)g=\gcd(a,b)g=gcd(a,b),则函数对 ttt 的最小重复周期为T=2πg, T=\frac{2\pi}{g}, T=g2π,
曲线在一个周期内完成闭合。
-
频率比为无理数(致密):若 ab\frac{a}{b}ba 为无理数,则轨迹不会闭合,而是在某区域内稠密填充(随采样时间越长越像填满区域)。
3. 仪器学意义(示波器上的应用)
-
在示波器的 X-Y 模式下,将一通道接 x(t)x(t)x(t)、另一通道接 y(t)y(t)y(t),李萨如图直接给出两信号间的频率比与相位差信息:
-
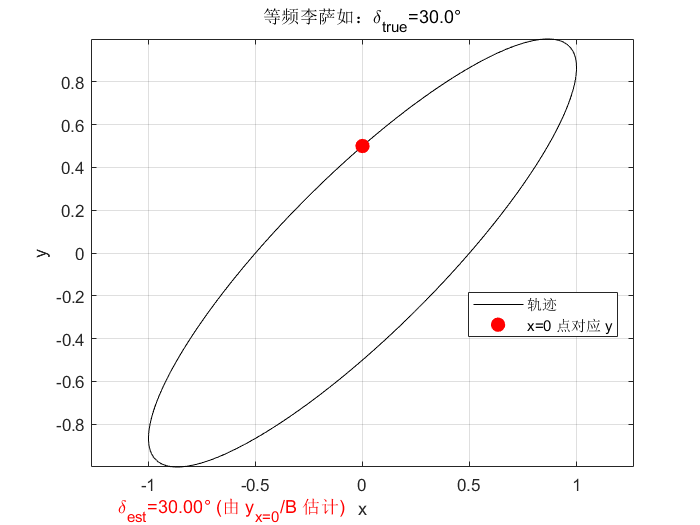
若频率相同 (a=ba=ba=b),用 xxx-轴过零点时 yyy 的截距可估相位:当 x=0x=0x=0(即 sin(at)=0\sin(at)=0sin(at)=0)时 y=Bsinδy=B\sin\deltay=Bsinδ,因此
δ=arcsin (yat x=0B), \delta=\arcsin\!\Big(\frac{y_{\text{at }x=0}}{B}\Big), δ=arcsin(Byat x=0),
这是示波器上常见的相位测量法(注意有符号与 π\piπ 的模糊,需要结合方向或多次测量判定象限)。
-
若频率比为简单整数比 m:nm:nm:n,图形的“瓣数/形状”可直接读出比例,从而判定频率比。
-
4. MATLAB 可视化代码(完整示例脚本)
下面给出一个自包含的 MATLAB 脚本 Lissajous_demo.m,它演示若干典型参数、整数比闭合与无理比稠密两类情形,并给出一个用于 等频情况估算相位差 的简单方法。
把下面代码复制到一个文件 Lissajous_demo.m,在 MATLAB 中运行即可。
% Lissajous_demo.m
% 李萨如图示例脚本:绘制若干典型参数并演示等频相位估计
clear; close all; clc;
% ------- 示例参数(每行:A B a b delta) delta 单位为弧度
examples = [
1 1 1 1 0; % 同频,同相 -> 直线
1 1 1 1 pi/2; % 同频,90度 -> 圆(若A=B)
1 1 2 1 0; % 频率比 2:1
1 1 3 2 pi/4; % 频率比 3:2 带相位
1 1 5 4 pi/3; % 频率比 5:4
1 1 1 sqrt(2) 0 % 无理比示例(稠密)
];
figure('Position',[100 100 1200 700]);
rows = 2; cols = 3;
for k = 1:size(examples,1)
A = examples(k,1); B = examples(k,2);
a = examples(k,3); b = examples(k,4); delta = examples(k,5);
% 智能选取绘制时间长度 t_end:
if abs(a-round(a))<1e-10 && abs(b-round(b))<1e-10
% 若 a,b 为整数,则最小重复周期 T = 2*pi / gcd(a,b)
g = gcd(round(a), round(b));
T = 2*pi / max(g,1);
t_end = T; % 一个周期即可见闭合图形
N = 4000;
else
% 非整数(可能为无理比),用较长时间观察稠密性
t_end = 40*pi;
N = 20000;
end
% ------- 绘制李萨如图 -------
t = linspace(0,t_end,N);
x = A*sin(a*t + delta);
y = B*sin(b*t);
subplot(rows,cols,k);
plot(x,y,'LineWidth',1.2);
axis equal; grid on;
xlabel('x = A sin(a t + \delta)');
ylabel('y = B sin(b t)');
title(sprintf('A=%.2g B=%.2g, a=%.3g b=%.3g, \\delta=%.3g\\pi', ...
A,B,a,b,delta/pi));
end
sgtitle('李萨如图示例(不同频率比与相位)','FontSize',14);
% ------- 等频(a==b)时的相位估计演示 -------
figure('Name','等频相位估计示例','NumberTitle','off');
A = 1; B = 1; a = 1; b = 1; delta_true = pi/6; % 30度
t = linspace(0,2*pi,5000);
x = A*sin(a*t + delta_true);
y = B*sin(b*t);
plot(x,y,'k'); axis equal; grid on;
xlabel('x'); ylabel('y');
title(sprintf('等频李萨如:\\delta_{true}=%.1f°', delta_true*180/pi));
hold on;
% 找到 x=0 处的第一个交点并内插算出对应 y 值(线性内插)
zc = find(x(1:end-1).*x(2:end) < 0, 1, 'first');
if ~isempty(zc)
kidx = zc;
% 线性内插求零点时刻 t0
t0 = t(kidx) - x(kidx)*(t(kidx+1)-t(kidx)) / (x(kidx+1)-x(kidx));
y0 = interp1(t,y,t0);
plot(0,y0,'ro','MarkerFaceColor','r','MarkerSize',8);
% 估计相位(取 principal branch)
delta_est = asin( y0 / B );
txt = sprintf('\\delta_{est}=%.2f° (由 y_{x=0}/B 估计)', delta_est*180/pi);
legend('轨迹','x=0 点对应 y','Location','best');
text(0.05, -0.1, txt, 'Units','normalized','FontSize',11,'Color','r');
fprintf('真实相位 (rad) = %.6f, 估计相位 (rad) = %.6f\n', delta_true, delta_est);
else
warning('未找到 x=0 的交点(采样/参数问题)');
end
% 保存示例图
% saveas(gcf, 'Lissajous_phase_estimation.png');
5. 李萨如图的应用
1. 频率比测量
李萨如图最经典的用途是在示波器上比较两个信号的频率。
-
原理:当两个互相垂直的输入信号分别驱动 X 轴与 Y 轴时,如果它们是正弦波,屏幕上会显示闭合的李萨如曲线。曲线形状与两个信号的频率比 a:ba:ba:b 有直接关系。
-
用途:通过观察图形的交点数目,可以快速判断频率比。例如:
- 频率比 1:1 → 圆、椭圆或直线
- 频率比 2:1 → “8” 字形
- 频率比 3:2 → 三叶形等
-
应用场景:
- 早期电子仪器中,用于校准信号源、音叉或振荡器频率
- 无需复杂数学计算,直接肉眼判断频率比
2. 相位差测量
-
原理:当两个信号的频率相同(a = b),李萨如图是椭圆,椭圆的倾斜程度与相位差 δ\deltaδ 相关。
-
用途:通过测量椭圆的截距比例,或者直接找 x=0x=0x=0 时的 yyy 值,就可以估算相位差。
-
应用场景:
- 测量电路中电压与电流的相位差
- 声学中测量麦克风信号的相位差
- 振动分析中比较两个传感器的时延
3. 双通道信号分析
- 在信号分析中,如果需要同时观察两个通道信号的同步性与波形关系,李萨如图提供了一个二维视图。
- 这比单独看两个时域波形更容易发现周期性关系或失真。
4. 机械振动与模式识别
-
原理:李萨如图可视化两个垂直方向上的运动。
-
应用:
- 在机械系统(如悬挂系统、桥梁、飞机机翼)中,用两个方向的位移信号绘制李萨如图,可以判断振动模式是否为简谐、是否存在耦合或共振。
5. 光学与激光扫描
- 在激光灯光秀、示教仪器中,利用两个正交方向的扫描信号(X 扫描、Y 扫描)叠加,就可以生成李萨如曲线的光学图案。
- 通过调节频率比与相位,可以产生艺术性的动态图案(音乐可视化、艺术装置等)。
6. 通信与调制分析
- 在调幅(AM)、调频(FM)、调相(PM)信号分析中,李萨如图可用于快速识别调制类型和参数。
- 在 IQ 调制解调中,李萨如图和星座图有一定联系,都利用正交分量作二维显示。
📌 总结:
李萨如图的核心价值就是用二维轨迹可视化两个信号的关系,尤其是频率比与相位差的测量。在示波器普及之前,它几乎是工程师的“必修技能”,现在虽然有更先进的频谱仪、相位计,但在教学、艺术和某些快速诊断中依然非常有用。























 1826
1826

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










