时域卷积定理和频域卷积定理，一图看懂卷积的过程！

时域卷积定理和频域卷积定理是信号与系统领域的重要定理，它们在时域和频域之间建立了卷积和乘积的对偶关系。以下是对两个定理的详细讲解：

1. 时域卷积定理

定义：
时域卷积定理表明，两个信号在时域上的卷积对应于它们在频域上的乘积。

数学公式：
设 $x(t)$ 和 $h(t)$ 是两个时域信号，其傅里叶变换分别为 $X(f)$ 和 $H(f)$。则：

$$x(t)\ast h(t)\stackrel{\mathcal{F}}{\leftrightarrow }X(f)\cdot H(f)$$

其中：

• $x(t)\ast h(t)$ 是 $x(t)$ 和 $h(t)$ 的卷积，定义为：

$$(x\ast h)(t)={\int }_{-\infty }^{\infty }x(\tau )h(t-\tau )d\tau$$

• $\stackrel{\mathcal{F}}{\leftrightarrow }$ 表示傅里叶变换的对应关系。

物理意义：

• 在时域中对两个信号进行卷积，相当于在频域中将其频谱逐点相乘。这说明卷积在频域中简化为代数运算。
• 应用场景：信号处理中的滤波，系统响应分析。

2. 频域卷积定理

定义：
频域卷积定理表明，两个信号在频域上的卷积对应于它们在时域上的乘积。

数学公式：
设 $X(f)$ 和 $H(f)$ 是两个频域信号，其对应的时域信号为 $x(t)$ 和 $h(t)$。则：

$$X(f)\ast H(f)\stackrel{{\mathcal{F}}^{-1}}{\leftrightarrow }x(t)\cdot h(t)$$

其中：

• $X(f)\ast H(f)$ 是 $X(f)$ 和 $H(f)$ 的频域卷积，定义为：

$$(X\ast H)(f)={\int }_{-\infty }^{\infty }X(f^{\prime })H(f-f^{\prime })d{f}^{\prime }$$

• $\stackrel{{\mathcal{F}}^{-1}}{\leftrightarrow }$ 表示逆傅里叶变换的对应关系。

物理意义：

• 在频域中对两个信号进行卷积，相当于在时域中将它们逐点相乘。这体现了频域和时域之间的对偶性。
• 应用场景：信号调制、系统带宽分析。

3. 两者的区别与联系

• 区别：时域卷积定理描述时域卷积与频域乘积的关系；频域卷积定理描述频域卷积与时域乘积的关系。
• 联系：二者体现了傅里叶变换的对偶性，时域和频域可以互相映射并简化运算。

4. 总结

• 时域卷积定理：时域卷积 ↔ 频域乘积
• 频域卷积定理：频域卷积 ↔ 时域乘积
  它们广泛应用于信号与系统分析、滤波器设计、通信系统等领域，帮助我们在时域与频域之间切换，选择更简单的计算方式。

通俗易懂地理解“卷积”

卷积本质上是一个“滑动叠加”的过程，类似于用一个函数去“扫描”另一个函数，计算它们在每个位置的重叠程度。下面用一个简单的例子来解释卷积的概念。

1. 想象一个场景

你有一个长长的窗户（代表函数 $h(t)$），可以移动窗户的位置；窗外是一个风景（代表函数 $x(t)$）。当窗户滑过风景时，你通过窗户看到了某个区域的景色，并对这部分的景色进行了加权求和。

2. 具体步骤

以时域卷积为例，两个信号 $x(t)$ 和 $h(t)$ 的卷积可以表示为：

$$(x\ast h)(t)={\int }_{-\infty }^{\infty }x(\tau )h(t-\tau )d\tau$$

这里的过程可以分为以下几步：

（1）翻转函数

先将函数 $h(t)$ 水平翻转（变成 $h(-\tau )$）。
这个翻转的步骤可以理解为“对准观察窗的一个固定端”。

（2）移动函数

将翻转后的 $h(-\tau )$ 按 $t$ 的位置移动（变成 $h(t-\tau )$）。
这一步相当于把窗户从左到右滑动，观察风景。

（3）点对点相乘

在每个位置，将 $x(\tau )$ 和 $h(t-\tau )$ 这两个函数的值点对点相乘。
就像在滑动窗户时，只看窗户覆盖部分的风景，并且对每一部分赋予权重。

（4）求和

把所有相乘后的结果求和，得到卷积结果 $(x\ast h)(t)$ 在当前位置的值。

3. 通俗比喻

• $x(t)$ 是一段道路上的信号，比如街道上某个时间段的车流量。
• $h(t)$ 是一个“模糊窗”，比如一个移动的平均滤波器（滑动窗口）。

你想知道在每一时刻，当这个“模糊窗”覆盖街道时，街道车流量的平均情况。
于是你用“模糊窗”去街道信号上滑动：

1. 每次叠加计算覆盖区域的车流量；
2. 然后移动窗户，重复这个过程。

最后得到的结果是一个新信号，反映了车流量的整体趋势，而不是瞬时的车流量。

4. 卷积的意义

卷积的本质是通过一个“模板”去分析信号的局部特性：

• $h(t)$ 可以看成是一个模板，描述我们关心的“形状”或“响应”。
• 滑动它，与 $x(t)$ 相互作用，来看看 $x(t)$ 在每个位置与模板的匹配程度。

5. 直观总结

• 卷积就像用一个窗户 $h(t)$ 去扫描一个风景 $x(t)$，记录窗户每次覆盖区域的重叠程度。
• 如果信号 $x(t)$ 和窗户 $h(t)$ 很匹配，卷积值就大；如果不匹配，卷积值就小甚至为零。

这样，卷积可以用来分析信号的变化趋势、平滑信号、提取特定特征等。

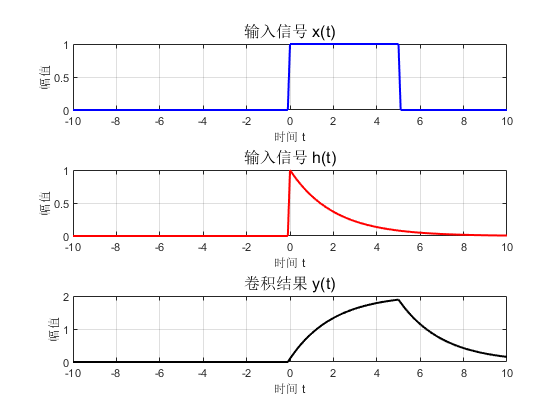
以下是用 MATLAB 可视化时域卷积过程的代码。这个例子会生成两个简单的函数并展示卷积过程的动画。

MATLAB 代码

% 清空工作空间
clear; clc; close all;

% 定义时间轴
t = -10:0.1:10;  % 时间范围
dt = t(2) - t(1); % 时间间隔

% 定义两个时域信号
x = double(t >= 0 & t <= 5);   % 信号x(t)，一个矩形脉冲
h = exp(-0.5 * t) .* (t >= 0); % 信号h(t)，一个指数衰减信号

% 计算卷积结果
y = conv(x, h, 'same') * dt;   % 卷积结果，归一化到时间范围

% 创建GIF文件名
gif_filename = 'convolution_animation_full.gif';

% 动画演示卷积过程
h_flipped = flip(h); % 翻转h(t)
h_shifted = zeros(size(t)); % 用于动态展示滑动

% 调整偏移量为整数
midpoint = round(length(t) / 2);

% 定义绘图窗口
figure('Color', 'w', 'Position', [100, 100, 1200, 800]); % 调整窗口大小

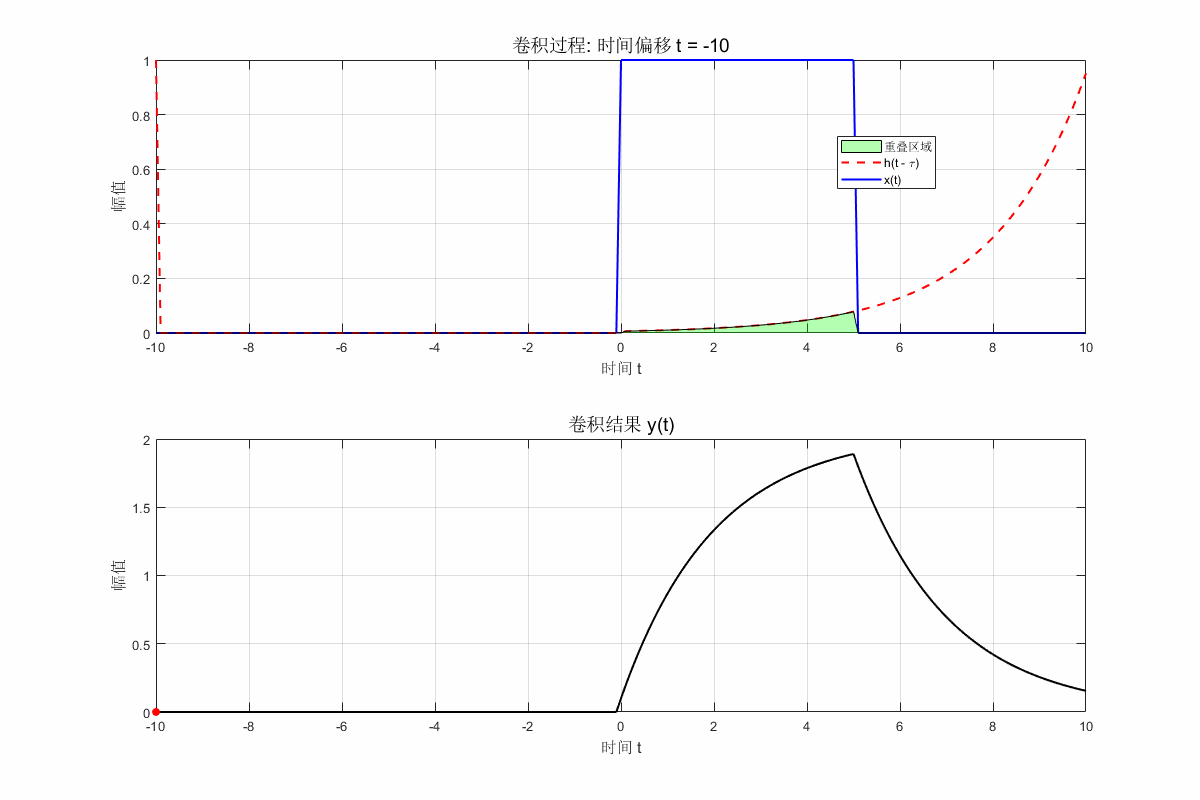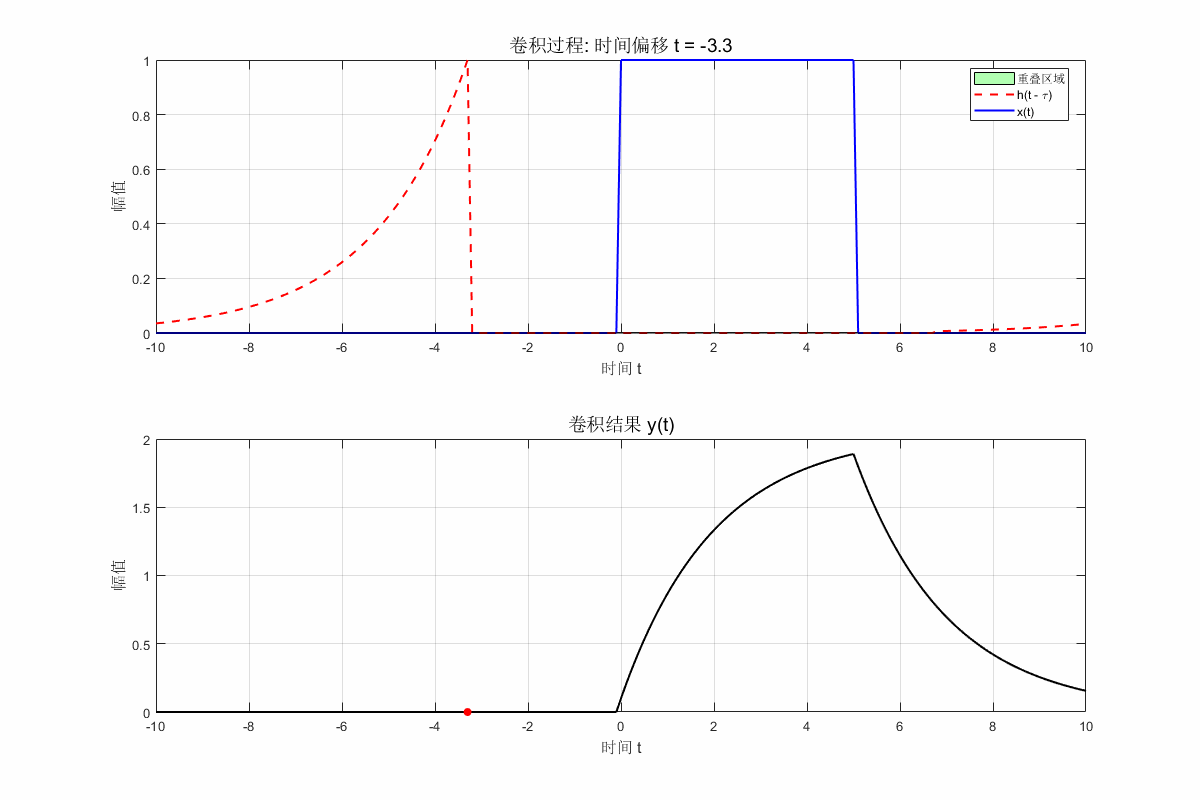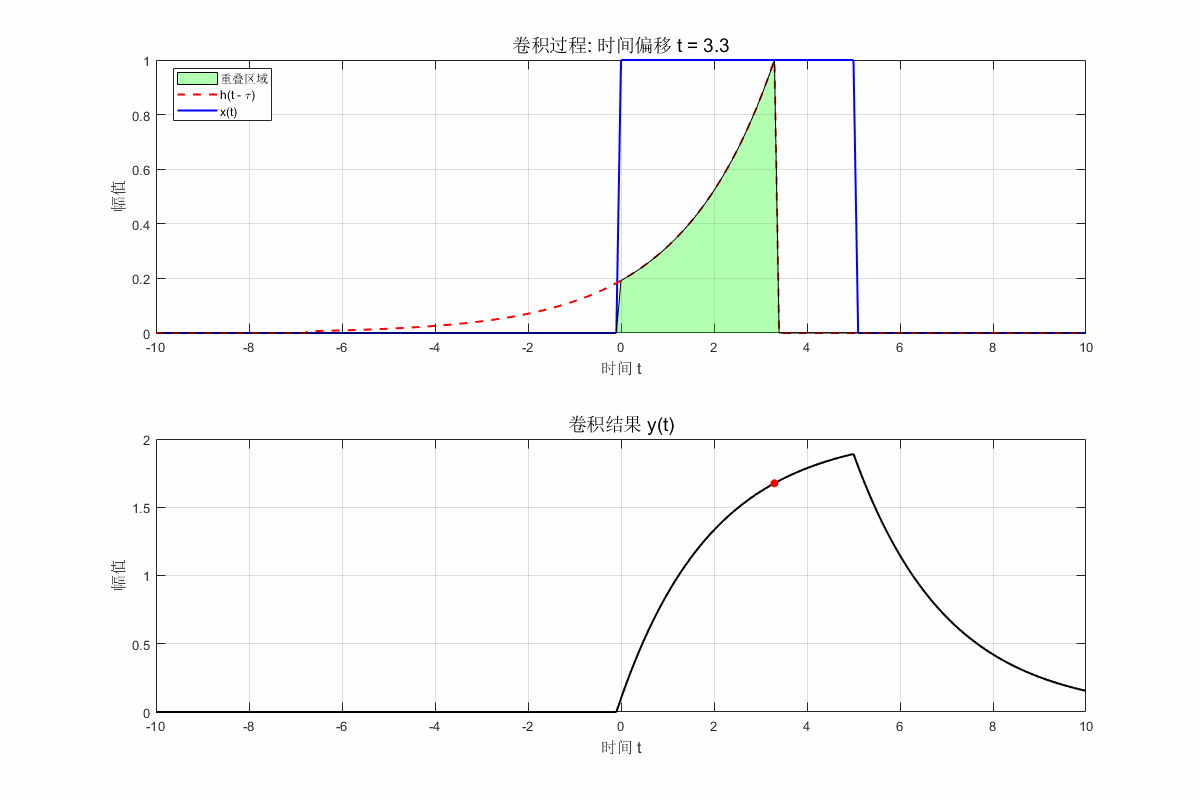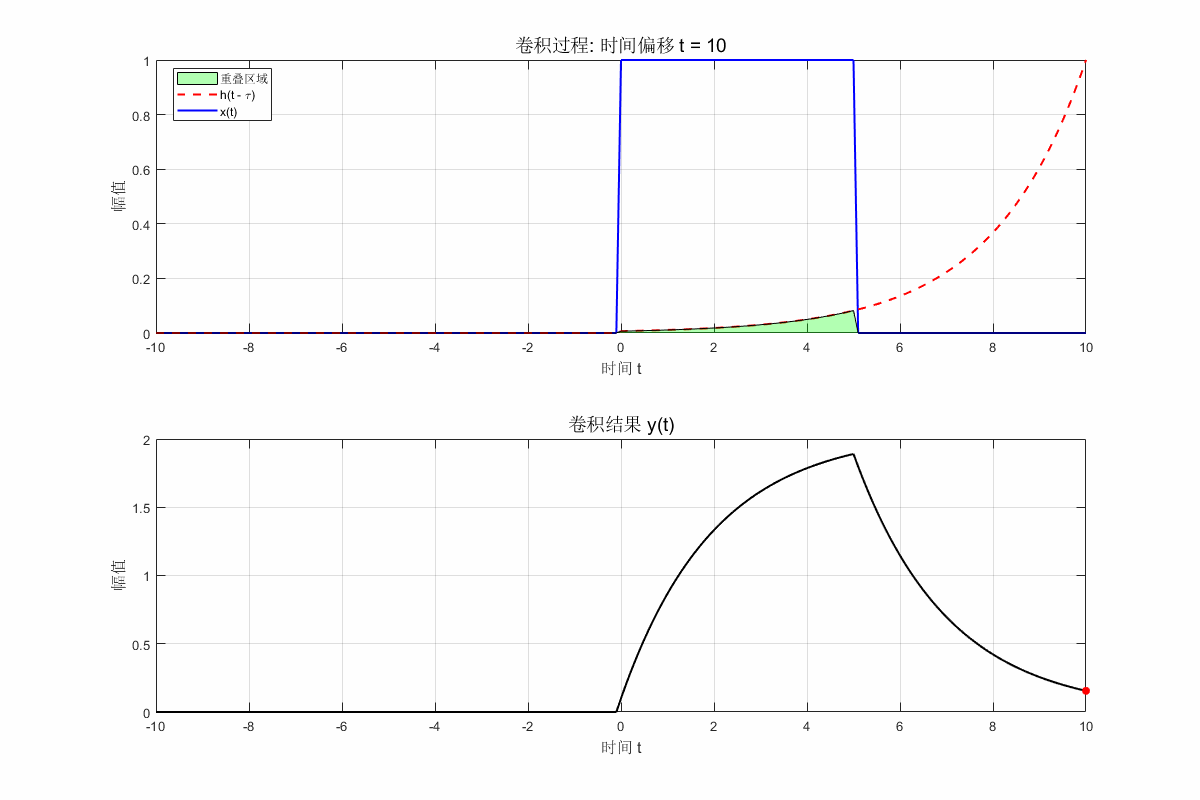
for i = 1:length(t)
    % 滑动翻转的 h(t)
    shift_amount = i - midpoint; % 计算滑动量
    h_shifted = circshift(h_flipped, shift_amount);
    
    % 点对点乘积
    overlap = x .* h_shifted;

    % 绘制当前帧
    clf; % 清除当前图像
    subplot(2, 1, 1);
    plot(t, x, 'b', 'LineWidth', 1.5); hold on;
    plot(t, h_shifted, 'r--', 'LineWidth', 1.5);
    area(t, overlap, 'FaceColor', [0 1 0], 'FaceAlpha', 0.3);
    title(['卷积过程: 时间偏移 t = ', num2str(t(i))], 'FontSize', 14);
    xlabel('时间 t', 'FontSize', 12); ylabel('幅值', 'FontSize', 12);
    legend('x(t)', 'h(t - \tau)', '重叠区域', 'Location', 'Best');
    grid on;

    subplot(2, 1, 2);
    plot(t, y, 'k', 'LineWidth', 1.5); hold on;
    scatter(t(i), y(i), 'ro', 'filled'); % 显示当前卷积值
    title('卷积结果 y(t)', 'FontSize', 14);
    xlabel('时间 t', 'FontSize', 12); ylabel('幅值', 'FontSize', 12);
    grid on;

    % 捕获当前帧
    frame = getframe(gcf); % 获取整个绘图窗口内容
    img = frame2im(frame); % 转换为图像

    % 将当前帧写入GIF
    [A, map] = rgb2ind(img, 256); % RGB 转换为索引图像
    if i == 1
        imwrite(A, map, gif_filename, 'gif', 'LoopCount', Inf, 'DelayTime', 0.05);
    else
        imwrite(A, map, gif_filename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.05);
    end
end

disp(['完整 GIF 已保存到当前目录：', gif_filename]);