计算机视觉ch3 图像到图像的映射——单应性变换

环境准备： matplotlib库安装教程

对图像块应用仿射变换，本文将图像或者图像的一部分放在另一幅图像中，使得它们能够和指定的区域或者标记物对齐

原理

1.单应性变换
单应性变换是将一个平面内的点映射到另一个平面内的二维投影变换。
单应性变换具有很强的实用性，比如图像配准、图像纠正和纹理扭曲，以及创建全景图像。
按照下面的方程映射二维中的点：

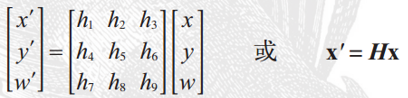
点的齐次坐标是依赖于其尺度定义的，所以x=[x,y,w]=[αx,αy,αw]=[x/w,y/w,1]都表示同一个二维点。
因此，单应性矩阵H也仅依赖于其尺度定义，所以，单应性矩阵具有8个独立的自由度，这样点具有唯一的图像坐标x和y，这个额外的坐标使得我们可以简单的使用一个矩阵来表示变换。

进行点和变换的处理时，我们会按照列优先的原则存储这些点，因此n个二维点集将会存储为齐次坐标意义下的一个3×n数组，这会使得矩阵乘法和点的变换操作变得更加容易，对于聚类和分类的特征，我们将使用典型的行数组来存储数据。

2.仿射变换
在上述的投影变换中，有一些特别重要的变换，比如仿射变换。

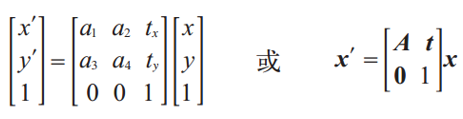
保持了w=1，不具有投影变换所具有的强大的变形能力。
仿射变换包含一个可逆矩阵A和一个平移向量t=[tx，ty]。

3.alpha通道