UVa 11019 - Matrix Matcher 【二维矩阵匹配_AC自动机】

Given an N ×M matrix, your task is to find the number of occurences of an X ×Y pattern.

Input

The first line contains a single integer t (t ≤ 15), the number of test cases. For each case, the first line contains two integers N and M (N,M ≤ 1000). The next N lines contain M characters each. The next line contains two integers X and Y (X,Y ≤ 100). The next X lines contain Y characterseach.

Output

For each case, output a single integer in its own line, the number of occurrences.

Sample Input

2
1 1
x
1 1
y
3 3
abc
bcd
cde
2 2
bc
cd

Sample Output
 

0
2

---

题意大意：从n*m的字符矩阵中找到有多少个x*y的字符矩阵。

---

思路：

我们对模式矩阵的每一行建trie树。 

corner[x][y]表示，以坐标(x, y)为右上顶点的大小和模式矩阵相等的矩阵中有多少行与模式矩阵对应相同。

 

 

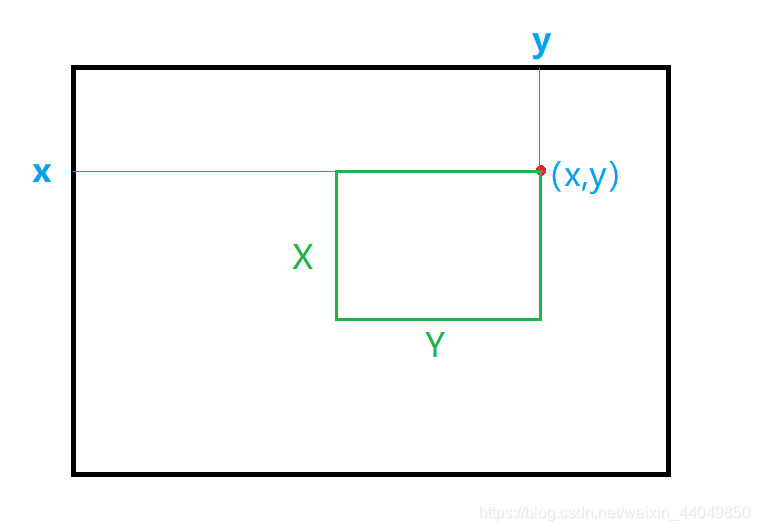
对于文本矩阵，我们对每一行的文本串进行处理，如果遇到模式串的结尾字符就进行corner[ ][ ]的更新。

• corner[ ][ ]更新时，我们需要考虑模式矩阵中是否有相同也就是重复的模式串。所以我用了一个vector[rt][ ]来存标号为rt的结尾结点对应的是第几行的模式串。比如vt[2][ ] = {1, 2}:就说明模式矩阵中的第一行和第二行相同啦~【因为要为了corner的比较容易更新，所以是字符矩阵是从标号1开始的啦~】

像是这样

ab
ab
cd

 

 

 

---

AC CODE 【附上更优的二维哈希解法】 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>

using namespace std;

const int maxN = 10004;
const int maxS = 1003;

struct AC_automat{
    int trie[maxN][26], tot;
    int fail[maxN], last[maxN];
    int edNum[maxN];
    vector<int>vt[maxN];
    int corner[maxS][maxS];

    void Clear(int rt)
    {
        for(int i = 0; i < 26; ++ i ) trie[rt][i] = 0;
        edNum[rt] = 0;
        vt[rt].clear();
    }

    void init()
    {
        Clear(0);
        tot = 0;
        memset(corner, 0, sizeof(corner));
    }

    void Insert(char *s, int p)
    {
        int rt = 0;
        for(int i = 0; s[i]; ++ i )
        {
            int id = s[i] - 'a';
            if(!trie[rt][id]) { trie[rt][id] = ++ tot; Clear(tot); }
            rt = trie[rt][id];
        }
        ++ edNum[rt];
        vt[rt].push_back(p);
    }

    void build()
    {
        queue<int>q;
        for(int i = 0; i < 26; ++ i )
            if(trie[0][i])
                q.push(trie[0][i]), fail[trie[0][i]] = last[trie[0][i]] = 0;
        while(!q.empty())
        {
            int rt = q.front(); q.pop();
            for(int i = 0; i < 26; ++ i )
            {
                int son = trie[rt][i];
                if(trie[rt][i])
                {
                    fail[trie[rt][i]] = trie[fail[rt]][i];
                    q.push(trie[rt][i]);
                    last[son] = edNum[fail[rt]] ? fail[rt] : last[fail[rt]];
                } else trie[rt][i] = trie[fail[rt]][i];
            }
        }
    }

    void getCorner(int nowH, int nowL, int ed)
    {
        int num = vt[ed].size();
        if(nowH)
        {
            for(int i = 0; i < num; ++ i )
            {
                if(nowH >= vt[ed][i])
                    ++ corner[nowH - vt[ed][i]][nowL];
            }
        }
    }

    void Find(char *t, int nowH)
    {
        int now = 0;
        for(int i = 0; t[i]; ++ i )
        {
            int id = t[i] - 'a';
            now = trie[now][id];
            if(edNum[now]) getCorner(nowH, i, now);
            else
            {
                int rt = now;
                while (last[rt]) getCorner(nowH, i, last[rt]), rt = last[rt];
            }
        }
    }

    void print(int n, int m, int x)
    {
        int ans = 0;
        for(int i = 0; i <= n; ++ i )
            for(int j = 0; j <= m; ++ j )
                if(corner[i][j] == x)
                    ++ ans;
        printf("%d\n", ans);
    }

}ac;

char str[maxS][maxS];
char t[102][102];

int main()
{
    int TAT; scanf("%d", &TAT);
    while(TAT -- )
    {
        int n, m; scanf("%d%d", &n, &m);
        for(int i = 1; i <= n; ++ i )
            scanf("%s", str[i]);
        int x, y; scanf("%d%d", &x, &y);
        for(int i = 1; i <= x; ++ i )
            scanf("%s", t[i]);
        if(x <= n && m >= y)
        {
            ac.init();
            for(int i = 1; i <= x; ++ i )
                ac.Insert(t[i], i);
            ac.build();
            for(int i = 1; i <= n; ++ i )
                ac.Find(str[i], i);
            ac.print(n, m, x);
        } else printf("0\n");
    }
    return 0;
}

/*
10
3 3
abc
bcd
bce
2 2
bc
cd
 */