机器学习单变量线性回归

首先，非常感谢斯坦福的教授吴恩达！！

1.假设函数（hypothesis fuction）
参数未知

2.代价函数（cost fuction）
又称平方误差函数
取1/2是为了后面的计算，求偏导省去，说白了就是为了少计算

3.决策函数
参数已得到，可进行预测

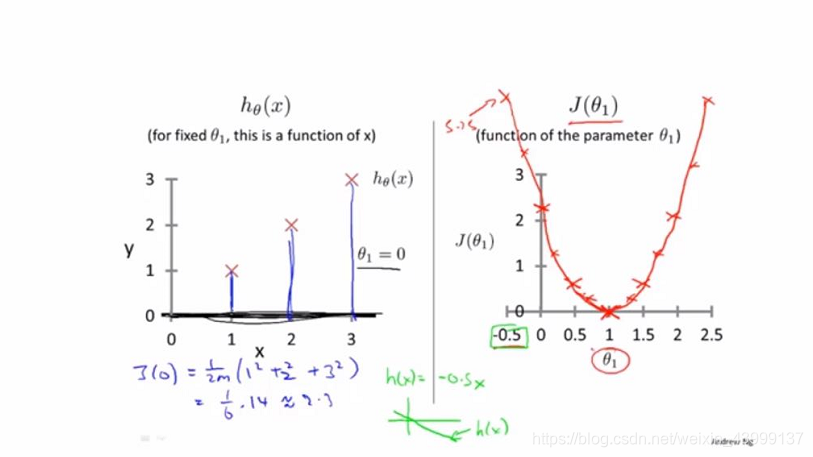
假设θ0取0，只讨论θ1，θ1的变化会导致代价函数的取值变大，我们想要的是代价函数小的时候的取值（即θ1取1的时候），这样得到的决策函数进行预测更加准确

4.梯度下降（非常重要的思想，求解参数，应用广泛，比最小二乘法还要广泛）

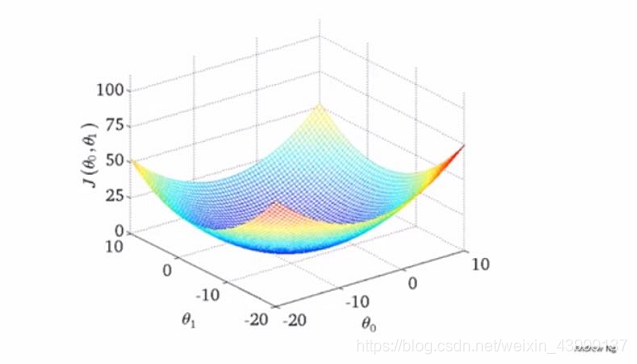
当两个变量同时讨论时，我们是在一个三维空间里面

但研究领域上更喜欢用等高线图（等高图像）contour plots

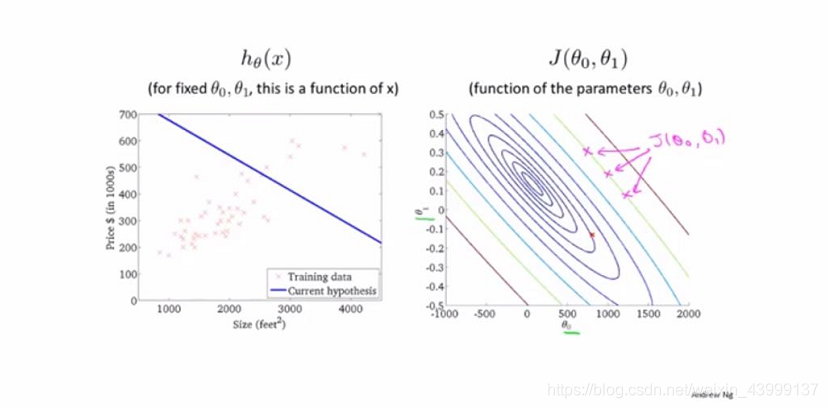
从上面的图可以清晰的看出取不同的θ0，θ1，得到的代价函数取值是有可能相同的

好的，关键来了！
如何取得最好的θ0和θ1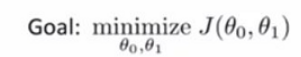

梯度下降的核心算法就是上图的第一条了
左下角是正确计算过程，右边则是错误计算过程
我们要遵循同时更新原则

核心算法中的α指的是学习率，这个是会根据实际情况进行调整的，但在求解θ时是不会变化的，但太大会可能跃过最低点，太小下降的则太慢

通过不断的迭代！！
最终到达最低点，因为最低点偏导数为0，所以反复迭代就能到达！！
此时的θ们就是我们想要的，使得代价函数最小，得到的决策函数预测更准确
这里用最小二乘法能解答，但面临复杂不能计算的问题或则更难的问题，最小二乘法是远远不够的，还是希望大家都能学会梯度下降！

附上简易的梯度下降求法：