线段树基础之影子的宽度

目录

怎么理解线段树

怎么用线段树

例题：影子的宽度

【高级数据结构】影子的宽度

题目描述

输入

输出

样例输入

样例输出

代码

总结

---

怎么理解线段树

那些题解百科里的都太复杂了，我就不引用了。

首先，“线段”怎么理解呢？ 在数学里，线段的定义是

线段（segment）是指两端都有端点，不可延伸，有别于直线、射线。

而在信息竞赛语言里，“两端都有端点”的线我们叫区间。

线段树，顾名思义，就是一棵每个节点都代表一个区间的树。

线段树（一般为二叉树）的每个父节点（非叶子节点）都表示他的所有子节点表示的区间的总区间。

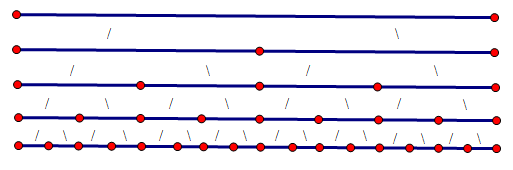如图

有什么好处呢？好处太多了等会儿就知道了。

怎么用线段树

例题：影子的宽度

前面都是废话这才是重点

【高级数据结构】影子的宽度

时间限制: 1 Sec  内存限制: 64 MB

题目描述

桌子上零散地放着若干个盒子，盒子都平行于墙。桌子的后方是一堵墙。如图所示。现在从桌子的前方射来一束平行光， 把盒子的影子投射到了墙上。问影子的总宽度是多少？

输入

第1行：3个整数L，R，N。-100000 <=L<=R<= 100000，表示墙所在的区间；1<=N<=100000，表示盒子的个数
接下来N行，每行2个整数BL, BR，-100000 <=BL<=BR<= 100000，表示一个盒子的左、右端点（左闭右开）

输出

第1行：1个整数W，表示影子的总宽度。

 

样例输入

Sample Input 1
0 7 2
1 2
4 5

Sample Input 2
-10 10 2
-5 2
-2 2


Sample Input 3
-10 10 3
-7 0
-4 9
-4 2


Sample Input 4
-100 100 3
-7 2
5 9
2 5

Sample Input 5
-50 50 4
-2 4
0 6
9 10
-5 30

样例输出

Sample Output 1
2

Sample Output 2
7

Sample Output 3
16

Sample Output 4
16

Sample Output 5
35

线段树解决

由于被平行光照射，所以桌子前后厚度忽略不计，就得到几个区间↓

不管前桌的影子还是后桌的影子都是影子，所以影子的总宽度就是这所有区间去重后的总长。

但是，如果单纯地把区间一一标记在一个数组里，太耗费时间了。如果能尽量把一个大区间直接标记为“有影子”，是不是方便很多呢？

所以就需要用到线段树了。

每次把一个区间插进去遍历，遇到合适的节点就标记它为“有影子”，这样就不用再管它的子节点了。

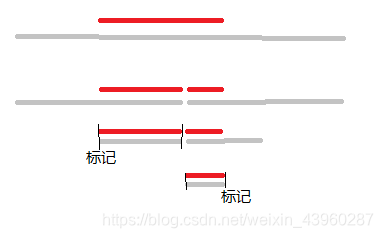每个节点的总覆盖量（“有影子”的总长度）就是它所有子节点的覆盖量的总和，最后输出根节点的覆盖量就完了。简单不？

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n,i,j,L,R,a,b,rmq[800000];
bool tr[800000];
inline int read(){         //读入优化
    int x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
void tongji(int l,int r,int i,int a,int b){
    int mid=(l+r)/2;
    if(l==a&&r==b){
        tr[i]=1;
        rmq[i]=r-l;
        return;
    }
    if(tr[i])return;
    if(a<mid&&!tr[i*2])tongji(l,mid,i*2,a,min(mid,b));
    if(b>mid&&!tr[i*2+1])tongji(mid,r,i*2+1,max(mid,a),b);
    rmq[i]=rmq[i*2]+rmq[i*2+1];
    return;
}
int main()
{
    L=read(),R=read(),n=read();
    for(i=1;i<=n;i++){
        a=read(),b=read();
        tongji(L,R,1,a,b);
    }
    printf("%d",rmq[1]);
    putchar('\n');
    return 0;
}

总结

void tongji(int l,int r,int i,int a,int b){
    int mid=(l+r)/2;
    if(l==a&&r==b){                                         //1
        tr[i]=1;
        rmq[i]=r-l;
        return;
    }
    if(tr[i])return;                                        //2
    if(a<mid&&!tr[i*2])tongji(l,mid,i*2,a,min(mid,b));      //3
    if(b>mid&&!tr[i*2+1])tongji(mid,r,i*2+1,max(mid,a),b);  //4
    rmq[i]=rmq[i*2]+rmq[i*2+1];
    return;
}

  ↑这里面的判断过程一定要记住，很常用！