Hilbert Sort（递归，dfs）

题目描述
The Hilbert curve, invented by the German mathematician David Hilbert, is one of the most famous fractal curves. The i-th Hilbert curve gives a sequential ordering of the cells in a 2ⁱ X2ⁱ grid.

The formal definition of Hilbert curves is recursive. The i-th Hilbert curve can be formed by connecting four (i-1)-th Hilbert curves, in the following way:

1. partition the 2ⁱ X 2ⁱ
   grid into four 2^i-1 X 2^i-1
   quadrants;
2. reflect an (i-1)-th Hilbert curve across the main diagonal (from top left to bottom right), and place it in the upper left quadrant;
3. place two copies of the (i-1)-th Hilbert curve in the lower left and lower right quadrants, respectively;
4. reflect an (i-1)-th Hilbert curve across the secondary diagonal (from top right to bottom left), and place it in the upper right quadrant.
   The first three Hilbert curves are shown below.

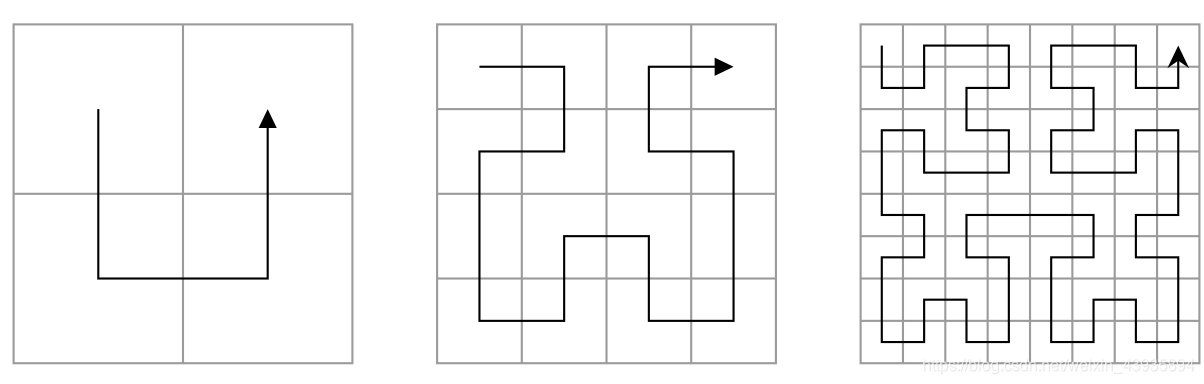
The Hilbert sort, just as the name implies, is to sort a set of the cells according to the Hilbert curve. A cell is ranked before another if it is encountered earlier when walking along the Hilbert curve. The Hilbert sort is widely used in many areas, because such sort maps a set of 2-dimensional data points into 1-dimensional space, with spatial locality preserved fairly well.

Give you an integer k and a set of cells in the 2^k X 2^k grid, please sort them in the order induced from the k-th Hilbert curve.

输入描述:
The first line contains two integers n, k (1≤n≤10
6 ,1≤k≤30), the number of cells to sort and the order of the Hilbert curve.

The next n lines, each containing two integers x_i,y_i(1≤x_i,y_i≤2^k ), denoting the cell in the x_i-th row and the y_i-th column. All cells in the input are distinct.

输出描述:
Output the coordinates of the sorted cells in n lines.

示例1
输入
5 2
2 4
2 3
1 1
3 1
4 3

输出
1 1
3 1
4 3
2 4
2 3

示例2
输入
4 1
1 1
1 2
2 1
2 2

输出
1 1
2 1
2 2
1 2

思路
将左上区域逆时针旋转90度，右上区域顺时针旋转90度，下方区域转移后递归实现

代码实现

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N=1000005;
typedef pair<int,int> P;

struct node
{
    int x,y;
    ll num;
}p[N];
bool cmp(node a,node b)
{
    return a.num<b.num;
}
ll searc(int k,int x,int y)
{
    if(k==0) return 1;
    int m=1<<(k-1);
    if(x<=m && y<=m) return searc(k-1,y,x);
    if(x>m && y<=m) return 3ll*m*m+searc(k-1,m-y+1,2*m-x+1);
    if(x<=m && y>m) return 1ll*m*m+searc(k-1,x,y-m);
    if(x>m && y>m) return 2ll*m*m+searc(k-1,x-m,y-m);
}
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d%d",&p[i].x,&p[i].y);
        p[i].num=searc(k,p[i].y,p[i].x);
    }
    sort(p,p+n,cmp);
    for(int i=0;i<n;i++)
    {
        printf("%d %d\n",p[i].x,p[i].y);
    }
    return 0;
}