- 多米诺和托米诺平铺
中等
304
相关企业
有两种形状的瓷砖:一种是 2 x 1 的多米诺形,另一种是形如 “L” 的托米诺形。两种形状都可以旋转。

给定整数 n ,返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。
平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同,当且仅当面板上有四个方向上的相邻单元中的两个,使得恰好有一个平铺有一个瓷砖占据两个正方形。
示例 1:
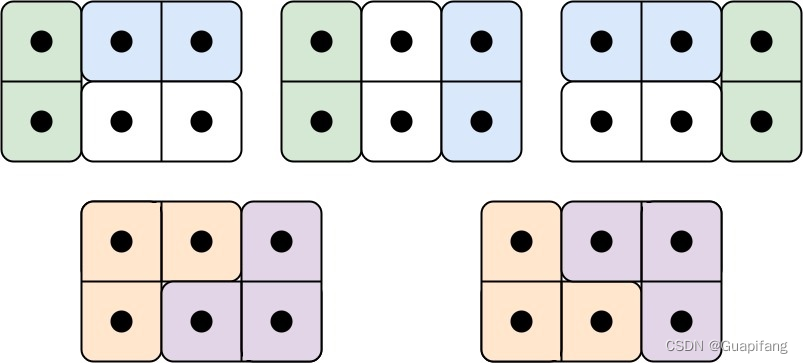
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。
示例 2:
输入: n = 1
输出: 1
提示:
1 <= n <= 1000
题解
这个题目很有意思呀,还好是规定了2xn的地板,不然难度会大不少。
我们考虑一下,在2xn的地板上,我们可以放的最后一块砖可以是啥类型的?
可以很简单的想到,有如下4种:

如果用B和D那么情况就会复杂一些,所以我们额外定义一个状态数组dp[1][x]和dp[2][x],dp[1][x]表示从左到右一直铺到第(1,x)位置的方案数,需要保证此时(2,x)位置为空。
如下所示,恰好和B对应上。

同时dp[2][x]表示从左到右一直铺到第(2,x)位置的方案数,需要保证此时(1,x)的位置为空,如下所示,恰好和D对应上。

定义cp[n]表示恰好铺完2xn所有地板的方案数。
如果最后一块用了B,那么cp[n] += dp[1][n-1];
如果最后一块用了D,那么cp[n] += dp[2][n-1];
如果最后一块用了A,那么cp[n] += cp[n-2];//这个应该很好理解。
如果最后一块用了C,那么cp[n] += cp[n-1];
所以最后的答案为:
AC代码
class Solution {
public:
typedef long long ll;
ll mod = 1e9 + 7;
ll dp[3][1005], cp[1005];
int numTilings(int n)
{
memset(dp,0,sizeof(dp));
memset(cp,0,sizeof(cp));
dp[1][2] = 1;
dp[2][2] = 1;
cp[0] = 0;
cp[1] = 1;
cp[2] = 2;
for(int i=3;i<=n;i++)
{
dp[1][i] = (cp[i-2] + dp[2][i-1])%mod;
dp[2][i] = (cp[i-2] + dp[1][i-1])%mod;
cp[i] = (cp[i-1] + cp[i-2] + dp[1][i-1] + dp[2][i-1])%mod;
}
return cp[n]%mod;
}
};
感觉是个很精巧的题目唉。。。。


























 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








