洛谷P1048 采药

题目描述
辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入输出格式
输入格式：
第一行有22个整数T(1 \le T \le 1000)T(1≤T≤1000)和M(1 \le M \le 100)M(1≤M≤100)，用一个空格隔开，TT代表总共能够用来采药的时间，MM代表山洞里的草药的数目。
接下来的MM行每行包括两个在11到100100之间（包括11和100100）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式：
11个整数，表示在规定的时间内可以采到的草药的最大总价值。

输入输出样例
输入样例
70 3
71 100
69 1
1 2
输出样例
3
——摘自洛谷
看了题，我一脸懵逼，这不是01一背包吗？在读一遍题，我相信我没看错。
01背包已经在另一篇里讲过了。但这次是论证DFS与动态规划的差别。
首先是DFS：

#include<bits/stdc++.h>
using namespace std;
int a[1000],b[1000];
int ans=0;
int n,m;
void dfs(int s,int ss,int x){
	if(x>n){
		ans=max(ans,ss);
		return ;
	}
	if(s+a[x]<=m){
		dfs(s+a[x],ss+b[x],x+1);
	} 
	dfs(s,ss,x+1);
}
int main(){
    cin >> m >> n;
	for(int i=1;i<=n;i++){
		cin >> a[i]>>b[i];
	}	
	dfs(0,0,0);
	cout << ans;
 	return 0;
}

结果。。。

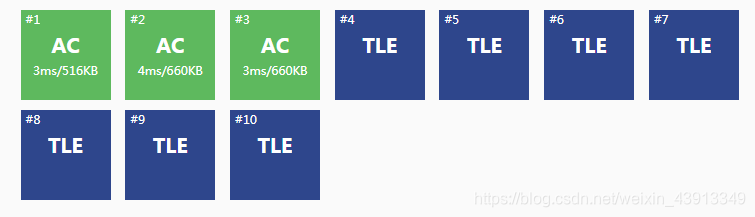
蒟蒻逃不过TLE的命运。。。（但我没试过记忆化搜索，可能记忆化搜索能过）
TLE的结果很明显，数据一大，深搜就要搜很多层，自然TLE。
那我们尝试一下DP的方式。

#include<bits/stdc++.h>
using namespace std;

int a[1010],b[1010];
int dp[1010][1010];
int n,m;
int v;
int main(){
	cin >> m>>n;
	for(int i=1;i<=n;i++){
			cin >> a[i]>>b[i];
	}
	for(int i=1;i<=n;i++){
		for(int j=m;j>0;j--){
		    if(a[i]<=j){
			dp[i][j]=max(dp[i-1][j],dp[i-1][j-a[i]]+b[i]); 
	    }else{
	    	dp[i][j]=dp[i-1][j];
	    	} 
		}
	}
	cout << dp[n][m];
	return 0;
}

嗯，AC了。
也就是说，爆搜代码简洁，但在数据范围小时，才能AC全部，但数据大时，DP更加有效。