【leetcode】 698 划分为k个相等的子集

var canPartitionKSubsets = function(nums, k) {
    /* 第一个s表示还有几个数字可用 */
    /* p表示当前这一份里面有几个 */
    /* 这个方法其实就是深搜，数组里的索引就代表一种排列组合，就好像dp32，代表每个数都选  */
    const dfs = (s, p) => {
        if (s === 0) {
            return true;
        }
 
        if (!dp[s]) {   //代表这个组合已经被选择过了
            return dp[s];
        }
        dp[s] = false;
        for (let i = 0; i < n; i++) {
            if (nums[i] + p > per) {      //如果当前选择超出了每个部分的和，就直接进行下一个选择
                break;
            }
            if (((s >> i) & 1) != 0) {  //如果他不等于0说明，这一位可用
                if (dfs(s ^ (1 << i), (p + nums[i]) % per)) {
                    return true;
                }
            }
        }
        return false;
    };
    const all = _.sum(nums);
    if (all % k !== 0) {
        return false;
    }
    per = all / k;
    nums.sort((a, b) => a - b);
    n = nums.length;
    if (nums[n - 1] > per) {
        return false;
    }
    /* 1左移n位 dp数组用来表示是否已经被用 */
    dp = new Array(1 << n).fill(true);
    return dfs((1 << n) - 1, 0);
}
var n = 5
console.log(1<<n)

感觉自己还是得多看看别人的代码，感觉别人写的好高级，在做这道题的时候，我去写了一下二分查找法和快速排序算法，发现自己简单的快排都不会写了，甚至发现我之前csdn里的博文竟然是错的，简直误人子弟。。。后续我会改掉。
这道题的解答里面用到了深搜，以及记忆化搜索，其实也不算什么深搜，就是找到一种遍历方法，这道题，只要找到一个可行通路，就是true。
算法思想，建立一个dp数组，数组的大小为原数组的排列组合种类，2的n次方，n为数组nums的元素个数。数组的值为true和false，用来记录这个组合是否可行。理解一下，其实这个dp数组，就是一个记忆数组，用来记录当前选择（为0的那几位）。如果要用数组记录的话，要费好多事，直接二进制数组记录好简单方便。。。

最近真的发现自己好缺大局观，比如在某一段代码里面，我能看懂某几行，但是我发现我缺少了把这几行代码整合起来的能力。可能是总结做的少了。

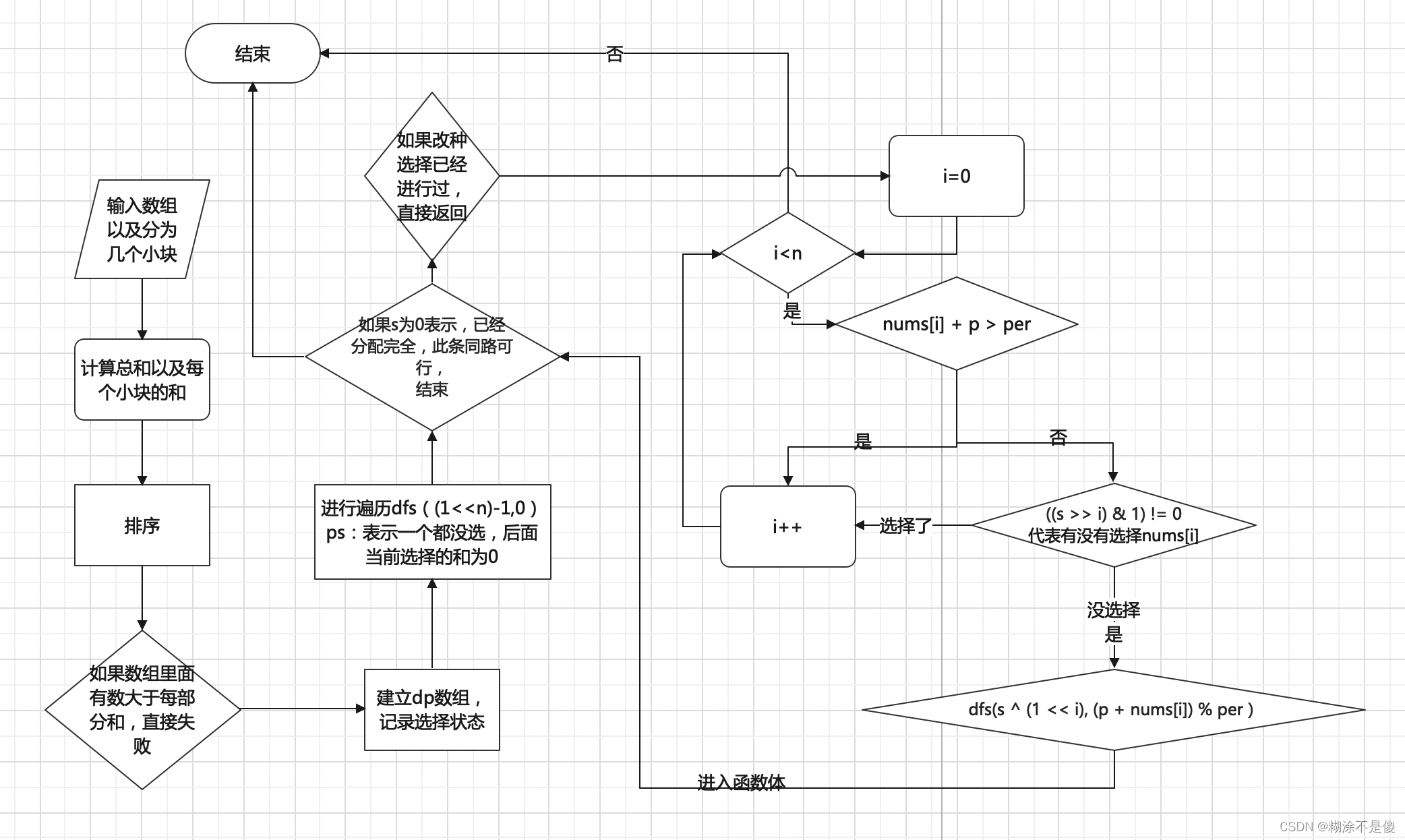
画的好捞。大致就是这个意思