在了解感知机之前的先知道1943年Mccilloch和Pitts所提出的M-P模型。
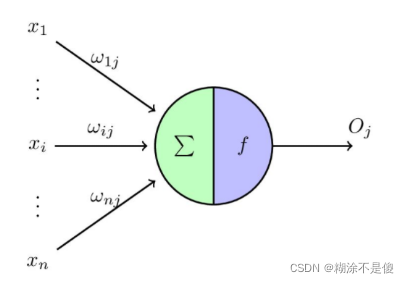
M-P模型其实就是现在的神经网络中的一个神经元,但是与之不同的点在于它没有非线性激活函数激活,也不能这么说,就是没有类似sigmoid或者tanh函数激活,而它用的仅仅是一个阈值去激活。
所以它的数学表达式为:
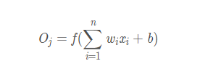
此处的f函数就是阈值函数。但是这里的权重w和偏置b都是人为设定的,并不存在学习一说,这就是M-P模型与单层感知器最大的区别。感知机中的权重w和偏置b是靠学习得来的。
接下来就是感知机学习算法的介绍。
对于误差,有一种方法是神经元的期望输出与实际输出之差,作为学习信号。
权重调整公式为:
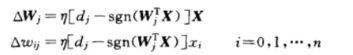
其中dj为期望输出,sgn为实际输出。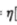 为控制学习速率的超参数。后面的xi为样本变量。
为控制学习速率的超参数。后面的xi为样本变量。
上代码!
# -*- coding: UTF-8 -*-
# numpy 支持高级大量的维度数组与矩阵运算import numpy as np
# Matplotlib 是一个 Python 的 2D绘图库import matplotlib as mpl
import matplotlib.pyplot as plt
#定义坐标,设定6组输入数据,每组为(x0,x1,x2) 三维输入
X=np.array([[1,4,3],
[1,5,4],
[1,4,5],
[1,1,1],
[1,2,1],
[1,3,2]]);
#设定输入向量的期待输出值 二分类 1和-1
Y=np.array([1,1,1,-1,-1,-1]);
#设定权值向量(w0,w1,w2),权值范围为-1,1 中间层为一个神经元 输入层为3个神经元 所以为3*1的矩阵
W = (np.random.random(3)-0.5)*2;
#设定学习率
lr = 0.3;#计算迭代次数
n=0;#神经网络输出
O=0;
def update(): #更新权重
global X,Y,W,lr,n;
n=n+1;
O=np.sign(np.dot(X,W.T));
#计算权值差
W_Tmp = lr*((Y-O.T).dot(X));
W = W+W_Tmp;
if __name__ == '__main__':
for index in range (100):
update()
O=np.sign(np.dot(X,W.T))
print(O)
print(Y)
if(O == Y).all():
print('Finished')
print('epoch:',n)
break
x1=[3,4]
y1=[3,3]
x2=[1]
y2=[1]
k=-W[1]/W[2]
d=-W[0]/W[2]print('k=',k)print('d=',d)
xdata=np.linspace(0,5)
plt.figure()
plt.plot(xdata,xdata*k+d,'r')
plt.plot(x1,y1,'bo')
plt.plot(x2,y2,'yo')
plt.show()





















 4142
4142










