29两数相除，递归求解

溢出是啥意思，我们都知道在计算机中，数使用二进制保存的，如

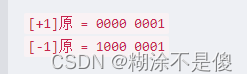
这个第一位就是符号位。计算机用补码保存数据，

所以会溢出。
用自己想出来的办法求解实在是太舒服了 虽然性能很差！
首先它有个32位有符号整数环境的前提，所以得把边角处理一下，
如果除数为-2^32：
被除数为1，结果就是它本身。
被除数为-1，结果为2^32-1
如果被除数为-2^32：
除数为-2^32，结果就是1。
除数为其他，结果为0
因为不能使用乘法除法以及mod运算，所以我用加减法，然后用除数dividend以次跟被除数的倍数d比较，但是不是一倍一倍往上增，而是1,2,4,8这种方式往上增（我们需要记录这个数count），就是前一个数是后一个数的2倍，（这里只需要用加法就可以）。
然后等到dividend<d的时候，我们用dividend-pred，这个pred就是前一个d在进行一次，直到这次count做出来是1.
要实现这一个算法，我们需要记录前一个和现在的d，count，我们分别用pred，d以及prec和c来记录。
步骤：
首先考虑溢出情况，
在考虑正负号，异号结果为负，同号为正
然后迭代：prec =0，count = 1，pred = 0，d = divisor
比较devident和d的大小如果dividend大，pred = d，d =d+d，prec = count，count=count+count
如果d大，迭代，但是要先保存prec，prec是此次的结果
最后把所有的prec相加。
用88和3举个例子：
第一次迭代，结果为16因为下一个d为96，大于88了
第二次迭代，结果为8
第三次迭代，结果为4
第四次迭代，结果为1（条件）
结束、

class Solution:
    def divide(self, dividend: int, divisor: int) -> int:
        if dividend == -2**32:
            if divisor==1:
                return -2**32
            if divisor == -1:
                return -2**32+1
        elif divisor == -2**32:
            if dividend == -2**32:
                return 1
            else:
                return 0
        if (divisor<0 and dividend<0) or (divisor>0 and dividend>0):
            flag =1
            dividend = abs(dividend)
            divisor = abs(divisor)
        else:
            dividend = abs(dividend)
            divisor = abs(divisor)
            flag = 0
        def recursion(dividend,divisor):
            if dividend<divisor:
                return [0]
            re = []
            prec =0
            count = 1
            pred = 0
            d = divisor
            while(dividend>=d):
                pred = d
                d = d+d
                prec = count
                count = count+count
            re.append(prec)
            re = re+recursion(dividend-pred,divisor)
            return re
        a = recursion(dividend,divisor)
        result = sum(a)
        if flag == 1:
            return result
        else:
            return -result




d = -21
ds = 1
a=Solution().divide(d,ds)
print(a)