leetCode最长回文串

暴力匹配法
解题思路：
1、首先得到一个字符串，先确定回文中心。
2、从回文中心向外扩展得到最大回文半径。
3、存储每一个元素作为回文中心时最大回文长度。
4、遍历完整个数组。
注意：情况要分奇偶，因为奇数和偶数时的回文中心不同。

解题时遇到的问题：当奇数最大回文中心和偶数最大回文中心一样时，需要考虑这种情况。

class Solution(object):
    def longestPalindrome(self, s):
        #violent match
        length = len(s)        #字符串数组长度
#stablish a array to record the length of palindrome when the center is anyone element of string
        lenP = [1]*length      #建立数组保存以各点为回文中心时的最大回文长度
#when the amount of element in string is odd;
        for i in range(0,length):    #回文中心
            j=0;    #用来保存当前的回文半径
            while((i-j>=0) & (i+j<length)):    #保证不超过数组大小
                if(s[i-j] == s[i+j]):
                    j+=1;
                else:
                    break;
            lenP[i] = j*2-1;
        mx = max(lenP)    #最大的回文长度
        argmax = lenP.index(max(lenP))    #最大回文长度时的回文中心索引
        result = s[int(argmax - ((lenP[argmax] - 1) / 2)): int(argmax + ((lenP[argmax] - 1) / 2) + 1)]    #记录当前结果


#when the amount of element in string is even
        for i in range(1,length):    #偶数部分，这里遍历从1开始可以避免只有一个的时候的情况
            if(s[i-1] == s[i]):
                j = 0;
                while ((i - j-1 >= 0) & (i + j < length)):
                    if (s[i - j-1] == s[i + j]):
                        j += 1;
                    else:
                        break;
                if(lenP[i] < j*2):
                    lenP[i] =j*2;
                if(lenP[i-1] < j*2):
                    lenP[i-1] = j*2;
        argmax1 = lenP.index(max(lenP))    #这边是更新最大长度的地方，避免因为更新完偶数部分最大长度变化未察觉
        if((argmax1 > argmax) | (lenP[argmax1]!=mx)):
            result = s[int(argmax1 - ((lenP[argmax1] - 2) / 2)):int(argmax1 + 1 + ((lenP[argmax1] - 2) / 2) + 1)]
        return result

java版本
两种方法有所不同，保存的不同，上面一种方法保存了全部中心的最大回文长度，下面的保存了最大的。

/**
* 5. 最长回文子串
*/
public class palindrome {
    public static String longestPalindrome(String s) {
        int start = 0;// 最长回文的起点
        int len = 0;// 最长回文的长度
        // 奇数
        for (int i = 0; i < s.length(); i++) {          //回文中心
            for (int j = 0; i - j >= 0 && i + j < s.length(); j++) {       //回文半径
                if (s.charAt(i - j) == s.charAt(i + j)) { //当回文最边缘点相同的时候
                    int tempLen = 2 * j + 1;         //当前回文长度回文长度
                    if (tempLen > len) {       //如果当前回文长度大于最大回文长度更新回文起点和长度
                        len = tempLen;    
                        start = i - j;
                    }
                } else {
                    break;
                }
            }
        }
        // 偶数
        if (s.length() > 1) {   //偶数是回文长度必须大于1
            for (int i = 0; i + 1 < s.length(); i++) {   //回文中心确定
                for (int j = 0; i - j >= 0 && i + 1 + j < s.length(); j++) {      //确定当前回文半径
                    if (s.charAt(i - j) == s.charAt(i + 1 + j)) {      //跟上述奇数一样
                        int tempLen = 2 * j + 2;
                        if (tempLen > len) {
                            len = tempLen;
                            start = i - j;
                        }
                    } else {
                        break;
                    }
                }
            }
        }
        return s.substring(start, start + len);
    }
    public static void main(String[] args) {     //静态函数只能调用静态函数
            // TODO Auto-generated method stub
            String a = longestPalindrome("aba");
            System.out.print(a);
      }
}

最后一个是manacher算法。
这个算法的优势在于，它将时间复杂度提升到了线性。

预处理部分：这一部分的目的在于解决回文中心是两个字母的问题，它的做法是在字符串的头部、尾部以及每两个字符的中间加上一个特殊字符以分隔两个一样的字符。例如： 原字符是“aa”，预处理完之后变成“#a#a#”

重要参数：
manacherString：预处理完之后的字符串。
回文半径和回文直径。
最右回文边界R： 在遍历字符串时，每个字符遍历出的最长回文子串都会有个右边界，而R则是所有已知右边界中最靠右的位置，也就是说R的值是只增不减的。换句话说，就是以所有回文中心的最大回文子串中最右边的元素。
回文中心C：就是回文的中间值
半径数组：以每一个字符为回文中心的最大回文长度。

算法步骤
1、预处理
2、R和C的初始值为-1，创建半径数组pArr
3、遍历字符串S
如果i在R右边，就暴力匹配然后更新R和C的值。
如果i在R左边，

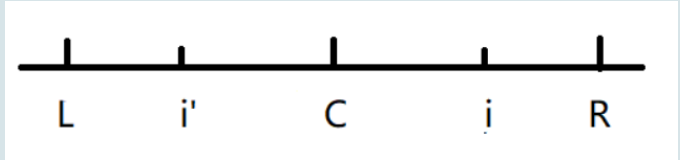
分3种情况：
①、i’的回文在L-R内部，此时i的回文直径跟i’的回文直径相同，我们可以直接得到i的回文直径。

②、超过了L，此时i的回文半径是i到R。

③、恰好重合，i的回文半径至少是i到R。可以继续扩展

Manacher算法的具体流程就是先匹配 -> 通过判断i与R的关系进行不同的分支操作 -> 继续遍历直到遍历完整个字符串

python代码：

msg = input("请输入你所想要找回文的字符串：")
#pretreatment 预处理 在每两个字符之间加上一个特殊字符'#'
length = len(msg)
manacherString = "#"
for i in range(0,length):
    manacherString = manacherString + msg[i]
    manacherString = manacherString + "#"
print(manacherString)


#开始创建关键未知数
R = -1   #最右回文边界
C = -1   #回文的中间值,最右回文边界的
pArr = [0]*(length*2+1)  #半径数组


#开始遍历整个数组，首先分两种情况，一种是i在R外，一种是i在R内
for i in range(0,2*length+1):
    if(i>R):   #当i在R外的时候，该情况因为R外的是都未扫描过的区域，所以直接进行暴力匹配法。
        j=0    #用于标识回文半径
        while ((i - j >= 0) & (i + j < 2*length+1)):
            if (manacherString[i - j] == manacherString[i + j]):
                j += 1
            else:
                break
        pArr[i] = j-1
        R = i+j-1
        C = i
    else:
        j = C - (i-C)    #i对于回文中心左边的元素
        L = C-(R-C)    #最右回文边界的元素
        if( (j-L)>pArr[j]):    #第一种情况子回文j均在L到R之间，该情况i的回文与j的回文相同
            pArr[i] = pArr[j]    
        elif((j-L)<pArr[j]):    #第二种情况，超过了L，那么回文半径是i到R
            pArr[i] = R-i
        elif((j-L)==pArr[j]):    #第三种情况，正好到L，那么i的回文半径可以继续去探索，此时要更新R和C
            j=R-i+1
            while ((i - j >= 0) & (i + j < 2*length+1)):
                if (manacherString[i - j] == manacherString[i + j]):
                    j += 1
                else:
                    break
            pArr[i] = j-1
            R = i + j-1
            C = i
print(pArr)
#下面就是把元素从manacherString 映射到msg上就可以了
argmax = pArr.index(max(pArr))
radius = (pArr[argmax]-1)/2
argmax = (argmax-1)/2
result = msg[int(argmax-radius):int(argmax+radius+1)]
print(result)