最小生成树(Minimum Spanning Tree)
经典的最小生成树算法的主要提出者是kruskal和prim,所以今天我们介绍的也是kruskal算法和prim算法。简单来说最小生成树就是用最少的代价使得一个图连通。
下面来拿个图来举例子
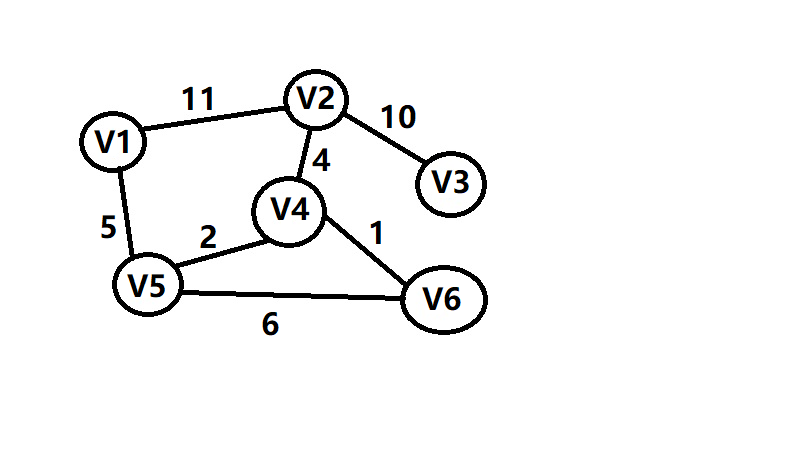
kruskal算法:
1:先对每条的权重按从小到大排序;
2:每次选取其中没有被选过的最小权重的边,并且不能形成环
3:一直搜索到边数=点数-1,如果不能则该图不连通
给出图示,便于理解
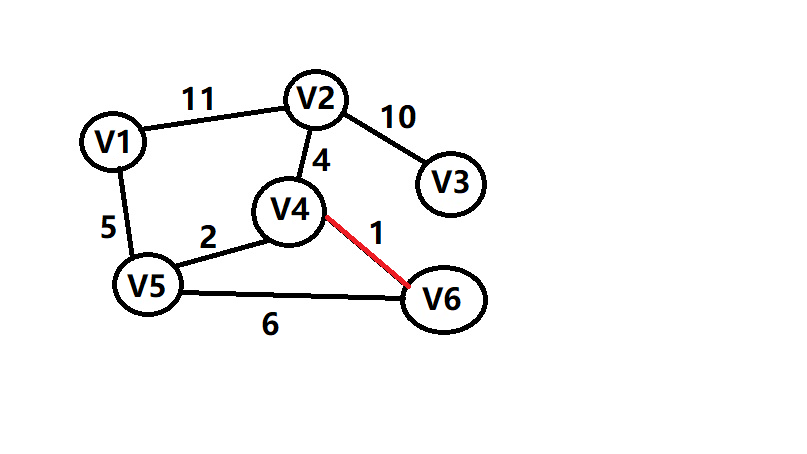
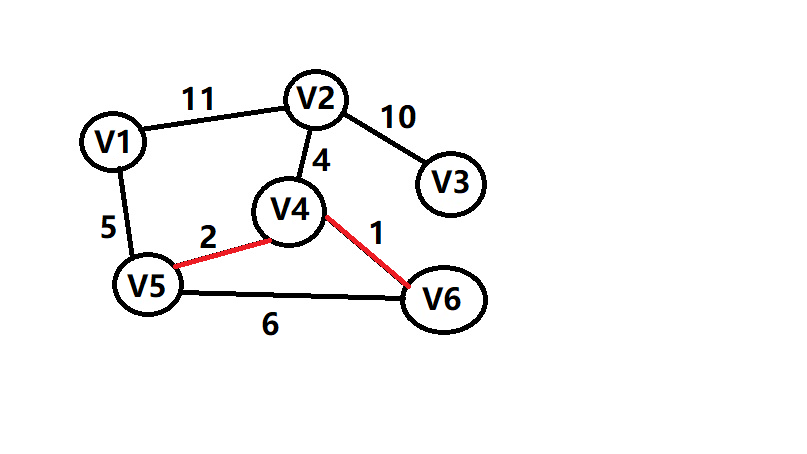
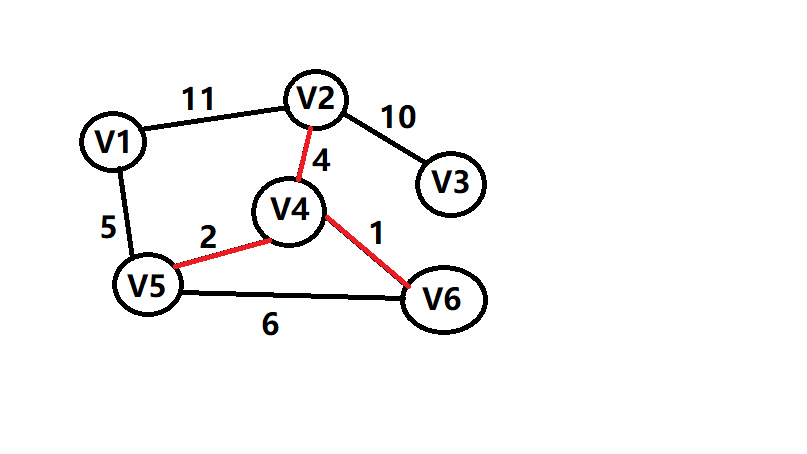
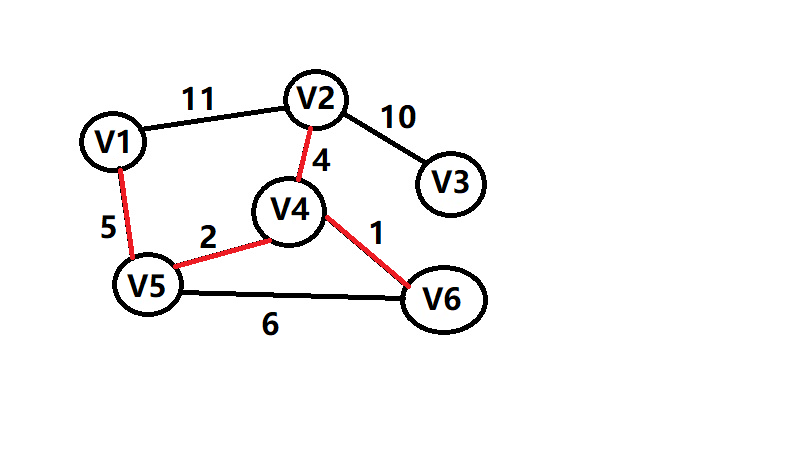
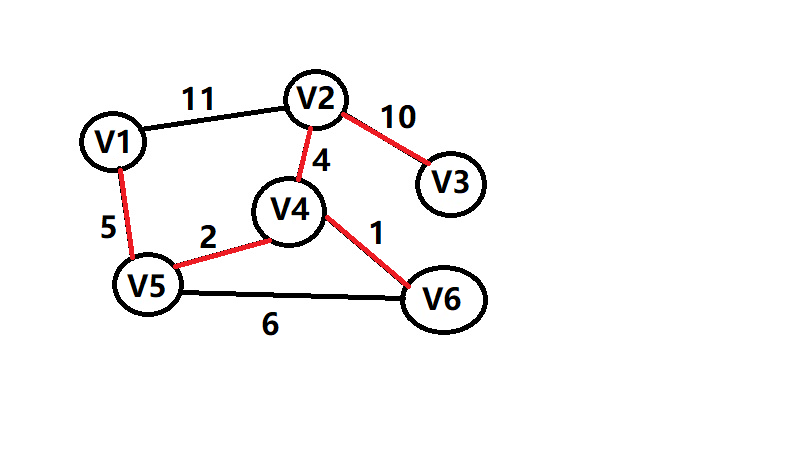
最后算出他的总代价sum=1+2+4+5+10=22 附上模板代码,大家可以在洛谷上进行测试https://www.luogu.org/problem/P3366
题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
输入格式
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式
输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
输入输出样例
输入 #1
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3
输出 #1
7
#include <bits/stdc++.h>
using namespace std;
const int maxn=200006;
int i,ans,n,m,cnt,ev,eu,fa[5005];
struct Edge{
int u,v,w;
}edge[maxn];
int find(int x)
{
while(x!=fa[x])
{
x=fa[x]=fa[fa[x]];//压缩路径
}
return x;
}
//并查集循环实现模板,及路径压缩,
bool cmp(Edge a,Edge b)
{
return a.w<b.w;
}
void kurska()
{
sort(edge,edge+m,cmp);
//将边的权值排序
for(i=0;i<m;i++)
{
eu=find(edge[i].u),ev=find(edge[i].v); //查看一条边的2点的连通状态
if(eu==ev) //如果2个点都已经连通了则跳过
continue;
ans+=edge[i].w;
fa[ev]=eu;
cnt++;
if(cnt==n-1) break;
}
}
int main()
{
cin>>n>>m;
for(i=0;i<=n;i++) //对父亲数组初始化
fa[i]=i;
for(i=0;i<m;i++)
{
cin>>edge[i].u>>edge[i].v>>edge[i].w;
}
kurska();
if(cnt==n-1) //如果满足边数==点数-1
cout<<ans;
else cout<<"orz"; //不连通
return 0;
}
prim算法:
1:先在图中任意选一个起点v1,放入集合VT
2:然后选取与VT中的点相连的未被选取过且使得边权最小的点,加入VT
3:然后重复步骤2直到所有点都被选取
再给个图吧
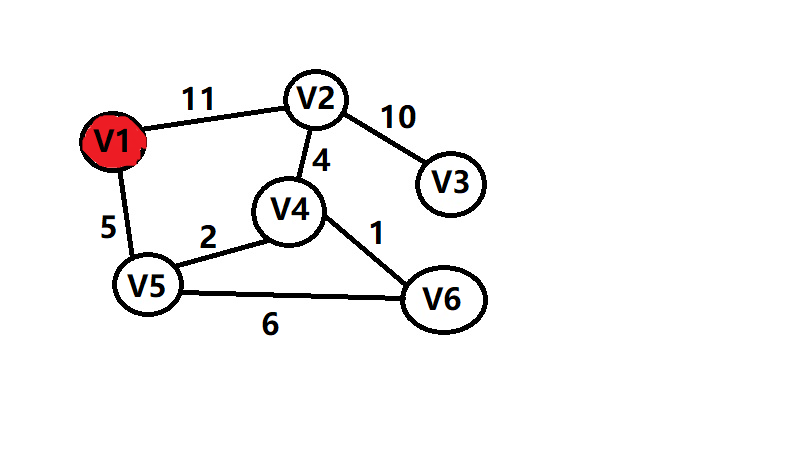
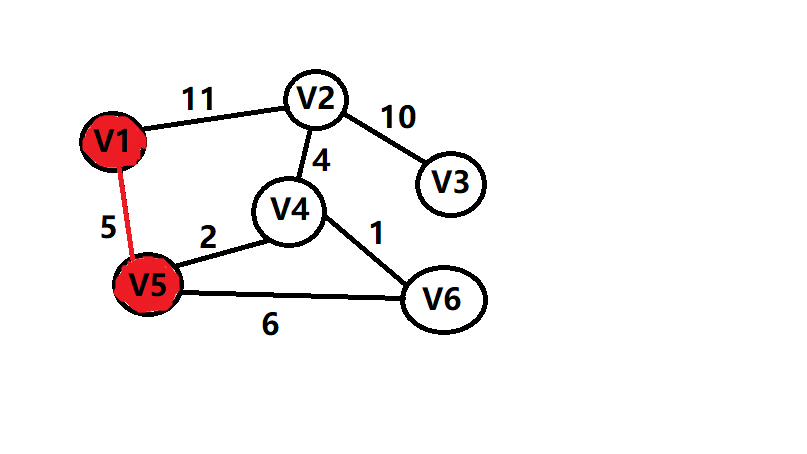
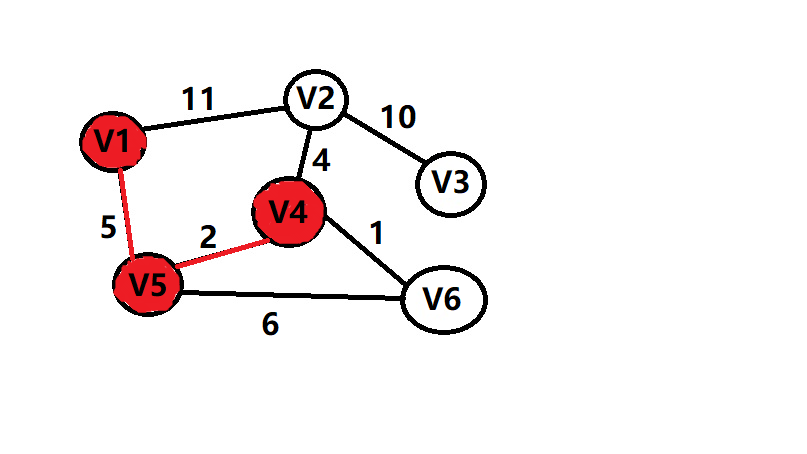
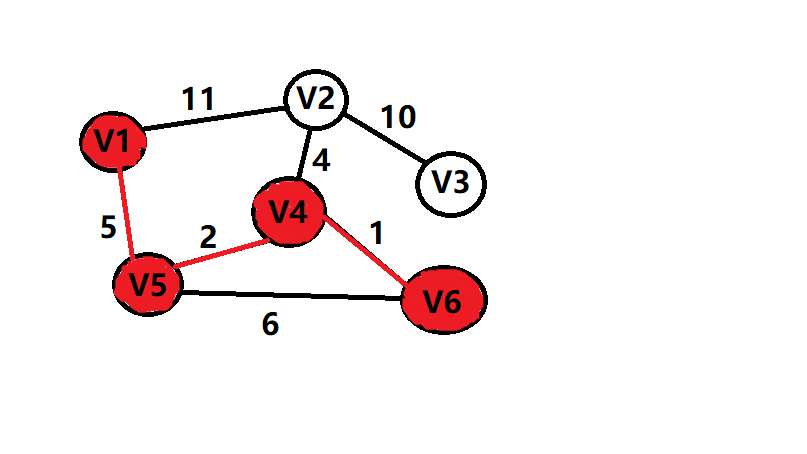
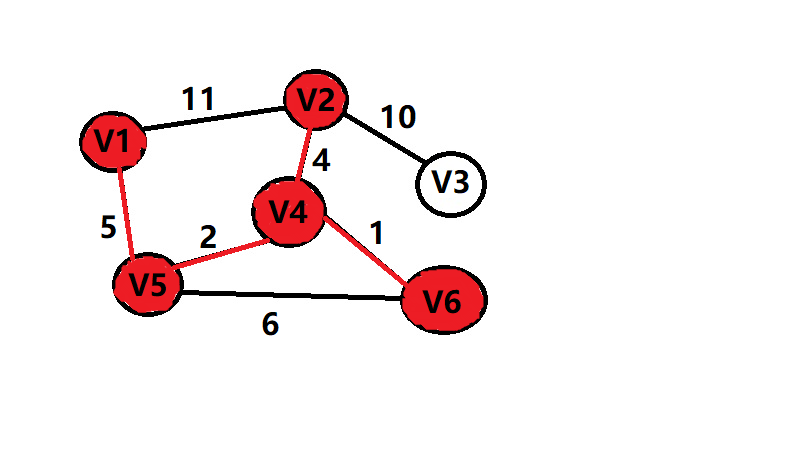
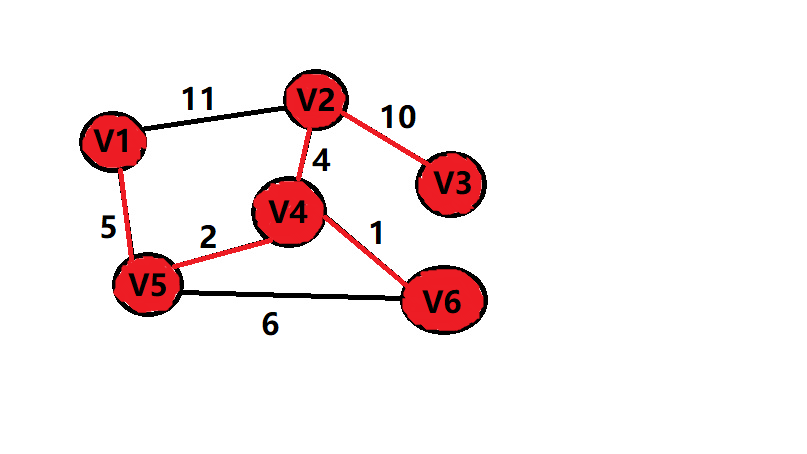
sum=5+2+1+4+10=22
再给一个参考别人的模板代码
#include<bits/stdc++.h>
using namespace std;
#define inf 123456789
#define maxn 5005
#define maxm 200005
struct edge
{
int v,w,next;
}e[maxm<<1];
//注意是无向图,开两倍数组
int head[maxn],dis[maxn],cnt,n,m,tot,now=1,ans;
//已经加入最小生成树的的点到没有加入的点的最短距离,比如说1和2号节点已经加入了最小生成树,那么dis[3]就等于min(1->3,2->3)
bool vis[maxn];
链式前向星加边
void add(int u,int v,int w)
{
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt;
//cout<<cnt<<endl;
}
int prim()
{
//先把dis数组附为极大值
for(int i=2;i<=n;++i)
{
dis[i]=inf;
}
//这里要注意重边,所以要用到min
for(int i=head[1];i;i=e[i].next)
{
dis[e[i].v]=min(dis[e[i].v],e[i].w);
}
while(++tot<n)//最小生成树边数等于点数-1
{
int minn=inf;//把minn置为极大值
vis[now]=1;//标记点已经走过
//枚举每一个没有使用的点
//找出最小值作为新边
//注意这里不是枚举now点的所有连边,而是1~n
for(int i=1;i<=n;++i)
{
if(!vis[i]&&minn>dis[i])
{
minn=dis[i];
now=i;
}
}
ans+=minn;
//枚举now的所有连边,更新dis数组
for(int i=head[now];i;i=e[i].next)
{
int v=e[i].v;
if(dis[v]>e[i].w&&!vis[v])
{
dis[v]=e[i].w;
}
}
}
return ans;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v,w;
cin>>u>>v>>w;
add(u,v,w),add(v,u,w);
}
printf("%d",prim());
return 0;
}




 本文介绍了最小生成树的概念及其在图论中的重要性,重点关注了Kruskal和Prim两种经典算法。Kruskal算法通过排序边权重并避免形成环路来构建最小生成树,而Prim算法则从一个起点开始逐步添加边,直至连接所有节点。文中提供了算法的解释、示例图和模板代码,帮助理解如何求解最小生成树问题。
本文介绍了最小生成树的概念及其在图论中的重要性,重点关注了Kruskal和Prim两种经典算法。Kruskal算法通过排序边权重并避免形成环路来构建最小生成树,而Prim算法则从一个起点开始逐步添加边,直至连接所有节点。文中提供了算法的解释、示例图和模板代码,帮助理解如何求解最小生成树问题。
















 1381
1381

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








