【最小生成树】

Prim算法

思路

以顶点为划分，U，与V-U两个阵营，循环纳入V-U中最靠近U的点，直到所有的点都在U中

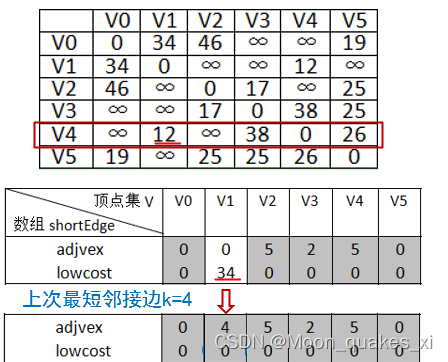
解释：

1.arc是邻接矩阵，表示了图中顶点与边的关系

1.lowcost为0时，代表该点（就是下标对应的点）已经在U中了

2.lowcost!=0时，adjvex（U）和下标（V-U）就表示U到V-U之间距离最近的边，lowcost为权值。

 基本步骤

1.找到最小的lowcost的下标 index

2.将index位置赋值为0 

3.遍历arc[index],如果有比sE.lowcost小的就覆盖 

#include<iostream>
using namespace std;
const int N=15;
struct shortEdge{
	int adjvex;
	int lowcost;
};
struct Edge{
	int from,to;
	int weight;
};

void getMinTree(int arc[N][N],shortEdge *sE,int n){
	for(int i=0;i<n-1;i++){
		int min=1e5,index=0,j;
		//找到最小的lowcost的下标 
		for(j=0;j<n;j++){
			if(sE[j].lowcost<min&&sE[j].lowcost!=-1&&sE[j].lowcost!=0){
				min=sE[j].lowcost;
				index=j;
			}
		}
		//将index位置赋值为0 
		sE[index].lowcost=0;
		//遍历arc[index],如果有比sE.lowcost小的就覆盖 
		//因为我这里把没有边的情况赋值成了-1 
		for(int k=0;k<n;k++){
			if(arc[index][k]!=-1&&(arc[index][k]<sE[k].lowcost||sE[k].lowcost==-1)){
				sE[k].lowcost=arc[index][k];
				sE[k].adjvex=index;
			}
		}
	}
	return;
}

int main(){
	int arc[N][N],n;
	cout<<"请输入顶点的个数"<<endl;
	cin>>n;
	cout<<"请初始化邻接矩阵(如果不能到达就赋值-1)"<<endl;
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			cin>>arc[i][j];
		}
	}
	shortEdge sE[N];
	for(int i=0;i<n;i++){
		sE[i].adjvex=0;
		sE[i].lowcost=arc[0][i];
	}
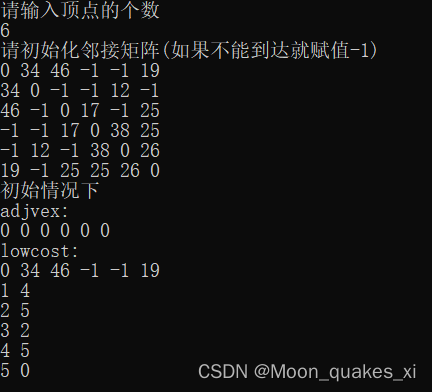
	cout<<"初始情况下"<<endl; 
	cout<<"adjvex:"<<endl; 
	for(int i=0;i<n;i++){
		cout<<sE[i].adjvex<<" ";
	} 
	cout<<endl<<"lowcost:"<<endl;
	for(int i=0;i<n;i++){
		cout<<sE[i].lowcost<<" ";
	} 
	cout<<endl;
	getMinTree(arc,sE,n);
	for(int i=1;i<n;i++){
		cout<<i<<" "<<sE[i].adjvex<<endl;
	}
	return 0;
	
}

 

 kruscal算法

思路

（是的，我来补kruscal了）

以边为划分，将点集合并（避免形成环），直到最后只剩一棵树。

 

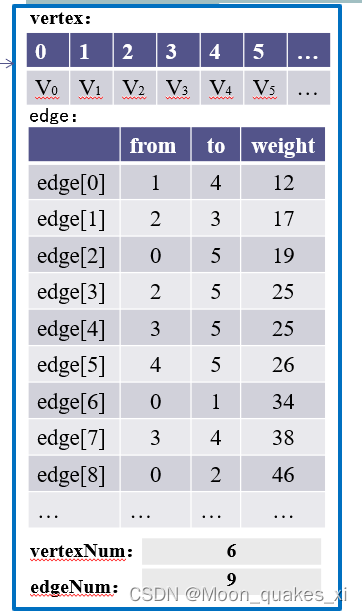
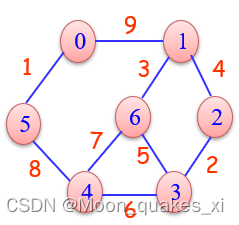
数据组织就是一个顶点表和递增的边表（当然顶点个数和边的个数）

处理思路：

1.依次访问边表（直接找到最小的边），如果两个顶点不在一个连通集就让to 那个顶点归顺from。

2.这里连通集的使用简化了操作：只要是在一个连通分量上的顶点都赋值为同一个根。

3.插排简单说一下思路：假定前面0-i已经排好序，就取i+1插入到前面的部分，插入位置（以从小到大排序为例）找到第一个大于i+1的地方。

#include<iostream>
using namespace std;
const int N=20;
struct Edge{
	int from,to;
	int weight;
};

struct EdgeGraph{
	int vertex[N];
	Edge edge[N];
	int verNum,edgeNum;
};

void getMinTree(int LT[],EdgeGraph EG,Edge minEdge[]){
	int el=0;
	int k=0;
	while(el<EG.verNum){
		if(LT[EG.edge[k].from]!=LT[EG.edge[k].to]){
			int tmp=LT[EG.edge[k].to];
			minEdge[el++]=EG.edge[k];
			for(int i=0;i<EG.verNum;i++){
				if(LT[i]==tmp) LT[i]=LT[EG.edge[k].from];
			} 
		}
		for(int i=0;i<EG.verNum;i++) cout<<LT[i]<<" "; 
		cout<<endl;
		k++;
	}
}


int main(){
	EdgeGraph EG;
	cout<<"请输入顶点的个数"<<endl;
	cin>>EG.verNum;
	for(int i=0;i<EG.verNum;i++){
		cin>>EG.vertex[i];
	} 
	cout<<"请输入边的个数"<<endl;
	cin>>EG.edgeNum;
	cout<<"请输入"<<EG.edgeNum<<"条边的信息"<<endl;
	cout<<"分别是：from、to、和weight"<<endl; 
	//我要边插边排 
	cin>>EG.edge[0].from>>EG.edge[0].to>>EG.edge[0].weight;
	for(int i=1;i<EG.edgeNum;i++){
		Edge p;
		int j;
		cin>>p.from>>p.to>>p.weight;
		for(j=0;j<i;j++){
			if(EG.edge[j].weight>=p.weight){
				for(int k=i-1;k>=j;k--){
					EG.edge[k+1]=EG.edge[k];
				}
				break;
			} 
		}
		EG.edge[j]=p;
	}
	cout<<"现在开始打印瞅一眼你输没有！"<<endl;
	cout<<"*****顶点*****"<<endl;
	for(int i=0;i<EG.verNum;i++) cout<<EG.vertex[i]<<" ";
	cout<<endl<<"*****边*****"<<endl;
	for(int i=0;i<EG.edgeNum;i++){
		cout<<EG.edge[i].from<<" "<<EG.edge[i].to<<" "<<EG.edge[i].weight<<endl; 
	}
	cout<<"打对啦！！！"<<endl;
	cout<<"Kruscal算法求最小生成树"<<endl;
	int LT[N];
	Edge minEdge[N];
	for(int i=0;i<EG.verNum;i++) LT[i]=EG.vertex[i];
	getMinTree(LT,EG,minEdge);
	cout<<"最小生成树为"<<endl;
	for(int i=0;i<EG.verNum-1;i++){
		cout<<minEdge[i].from<<" "<<minEdge[i].to<<" "<<minEdge[i].weight<<endl;
	}
}

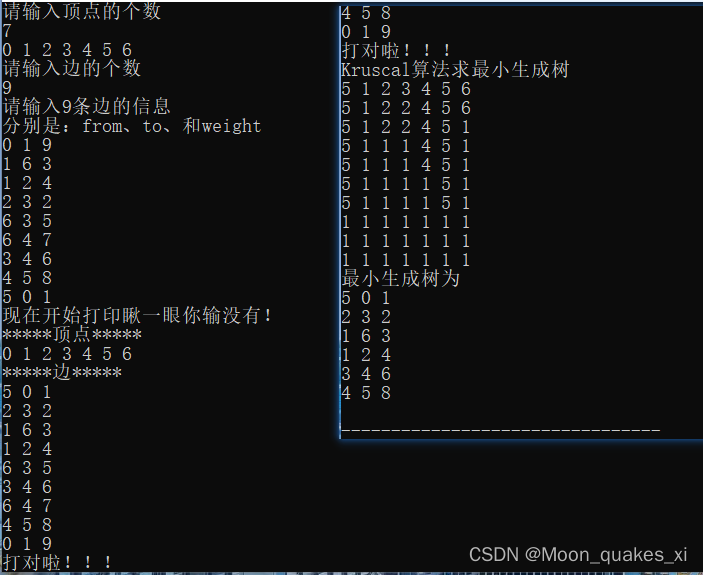
6.15日，我tmd以为老子之前写错了，结果没有，是图贴错了。