快速幂 简单易懂

当我们想要求解 xⁿ 的时候，通常我们使用的方法都是将 n 个 x 相乘，时间复杂度O(n)

在此基础上使用 快速幂 可以将时间复杂度将为O(log₂n)

对于任意一个十进制数字，都可以用二进制表示

• 例如4： 4 = 100 = 2²*1 + 2¹*0 + 2⁰*0
• 对于任意 n : n = b_m …b₂b₁b₀ = 2^m*b_m + … + 2²*b₂ + 2¹*b₁ + 2⁰*b₀

那么 xⁿ 就可以表示为：

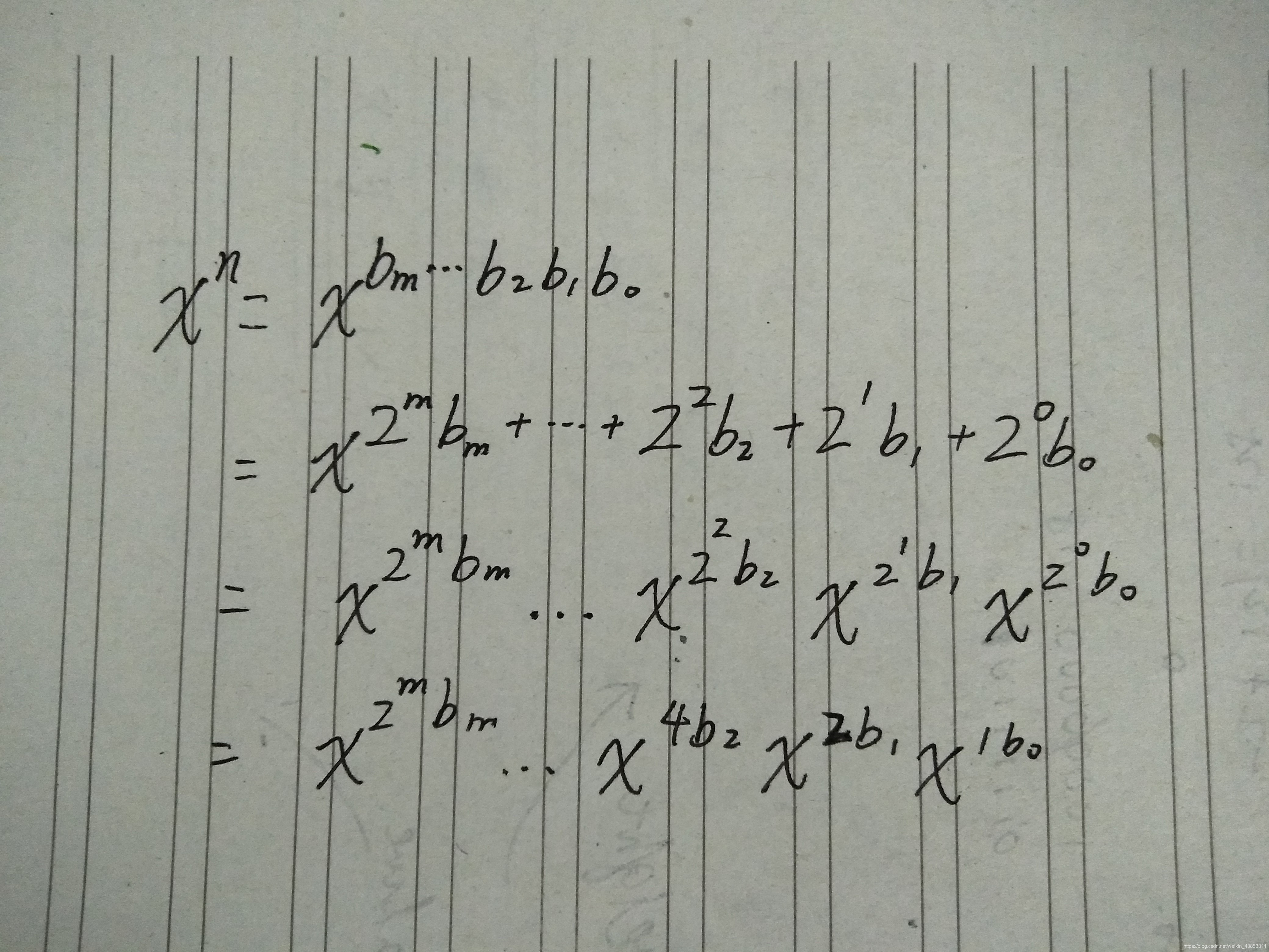
a = 2^m
b_m = 0 时，x^a 的值为 1
b_m = 1 时，x^a 的值为 x^a
接下来只需要计算 x¹、x²、x⁴…… 的值，再从 n 的二进制数最低位向最高位遍历。
若遍历的位是 1 则乘上 x^{此位的权重}， 是 0 则无操作

举个例子，要计算 3⁸
通常计算方法：3⁸= 3 * 3 * 3 * 3 * 3 * 3 * 3 * 3，需要 8 次计算
快速幂方法：
8 = 1000

• 从最低位开始遍历，temp 用来储存 x^a，result 用来储存结果
• 计算 temp = x¹ ，当前位为 0 ，不操作(1是当前位的权重)
• 计算 temp = x² 即 temp = temp²，当前位为 0，不操作(2是当前位的权重)
• 计算 temp = x⁴ 即 temp = temp²，当前位为 0，不操作(4是当前位的权重)
• 计算 temp = x⁸ 即 temp = temp²，当前位为 1，result = result * temp (8是当前位的权重)

只需要 4 次计算就可以得出结果

判断b^m是 0 还是 1 可以使用 与运算：b & 1
从低位向高位遍历可以使用移位：n >> 1

double qiuckPow(double x, int n) 
    {
        if(x == 0)    return 0;
        if(n < 0)		//这里对幂是负数作处理，转为正数的计算方法
        {
            n = -n;
            x = 1/x;
        }
        while(n > 0)
        {
            if(n & 1)  result = result * x;
            x = x * x;
            n = n >> 1;
        }
        return result;
    }