本文精选了算法竞赛中的经典题目，包括贪心算法、并查集、拓扑排序等技术的应用，通过具体案例解析，深入浅出地讲解了每种算法的实现原理和代码实现。
文章目录
A. Sea Battle（*800）（水题）
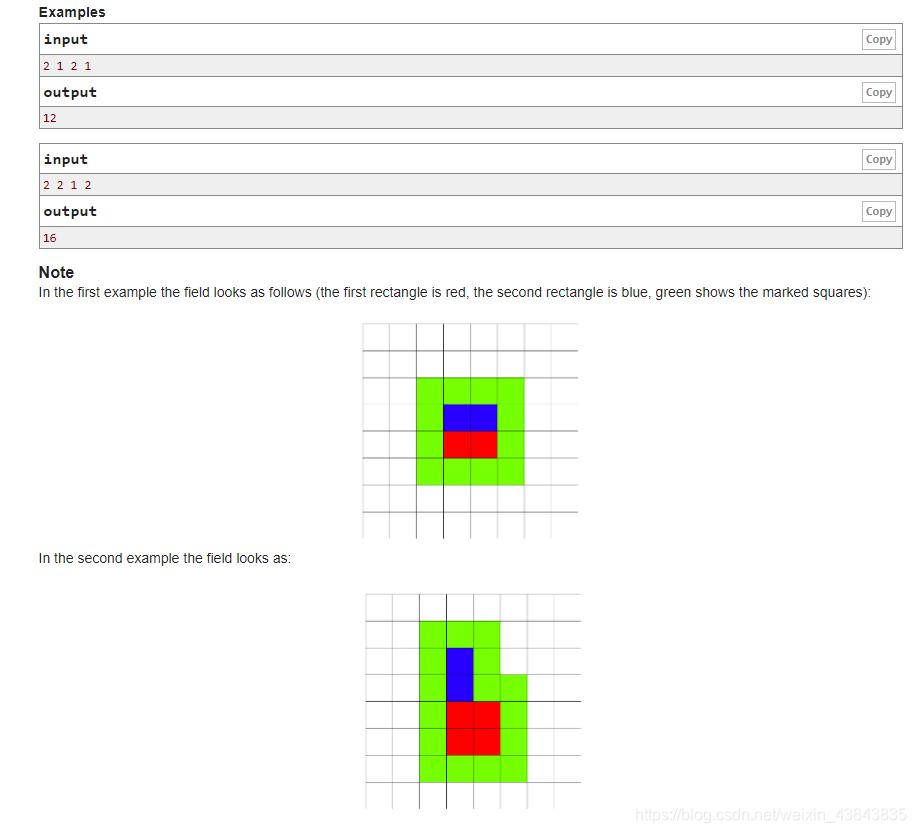
——题意——
给出两个矩形的长和宽，分别为
w
1
w1
w1,
h
1
h1
h1,
w
2
w2
w2,
h
2
h2
h2。两个矩形左侧对齐摆放，求出矩形周围一圈的绿色区块数。
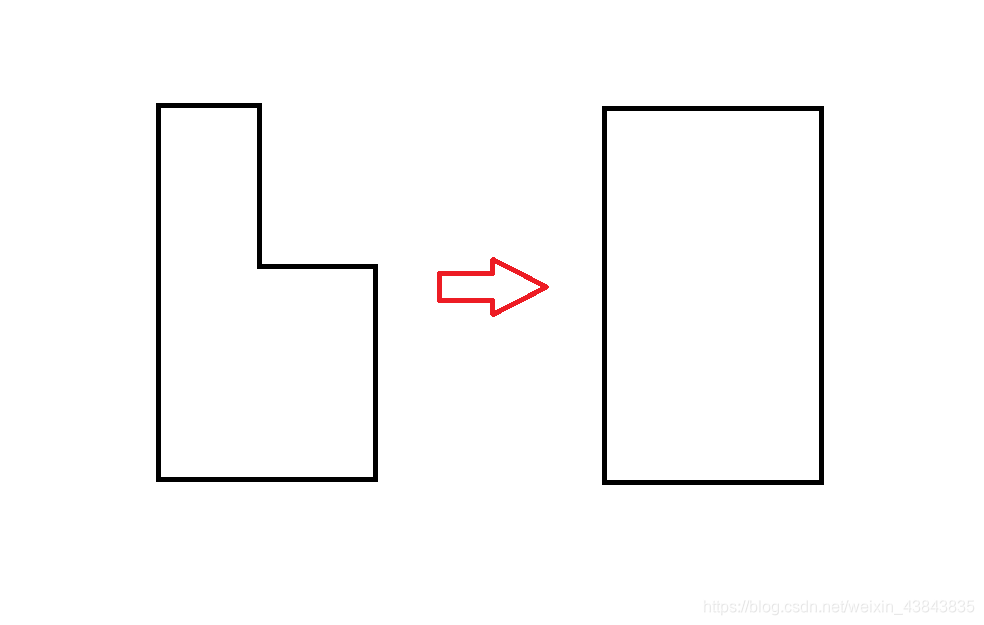
——题解——
小学数学知识，以下两个图形周长相等。
——Code——
#include<iostream>
using namespace std;
int main()
{
int w1,h1,w2,h2;
int ans=0;
cin>>w1>>h1>>w2>>h2;
ans=2*max(w1,w2)+2*(h1+h2)+4;
cout<<ans<<endl;
return 0;
}
B. Draw!（*1300）（水题）
——题意——
模拟足球比赛的得分，题目顺序给出一些阶段出现的分数，问最多出现多少次平分。
——题解——
按题目意思，一开始
0
:
0
0:0
0:0也算一种情况，初始化答案数为
1
1
1.
设上一次比分为
a
:
b
a:b
a:b，这一次比分为
x
:
y
x:y
x:y，那么可能的平分次数为
0
0
0或者是
m
i
n
(
x
,
y
)
−
m
a
x
(
a
,
b
)
min(x,y)-max(a,b)
min(x,y)−max(a,b),
具体还要区分
x
x
x和
y
y
y是否相等，
a
a
a和
b
b
b是否相等。
——Code——
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
int n;
int main()
{
int a=0,b=0;
int x,y;
cin>>n;
int ans=1;
for(int i=1;i<=n;++i)
{
cin>>x>>y;
if(x==a&&y==b) continue;
if(x==y&&a==b)
ans+=x-a;
else if(x==y&&a!=b)
ans+=1+x-max(a,b);
else if(x!=y&&a==b)
ans+=min(x,y)-a;
else
ans+=max(0,1+min(x,y)-max(a,b));
a=x;
b=y;
}
cout<<ans<<endl;
return 0;
}
C. Birthday（*1200）（贪心）
——题意——
给出
n
n
n个孩子的身高，要求把他们排成一个环，输出相邻两个孩子升高差最小的情况。
——题解——
很明显是个贪心，先按照从小到大的顺序对所有孩子身高排序，把最高的放在中间，在把次高的依次插在序列的两端。
——Code——
#include<iostream>
#include<algorithm>
using namespace std;
int n;
int a[102];
int ans[102];
int main()
{
cin>>n;
for(int i=1;i<=n;++i)
cin>>a[i];
sort(a+1,a+n+1);
if(n&1)
{
int mid=(n+1)/2;
ans[mid]=a[n];
for(int i=n-1;i>=2;i-=2)
{
int ab1=max(ans[mid]-a[i],ans[n-mid+1]-a[i-1]);
int ab2=max(ans[mid]-a[i-1],ans[n-mid+1]-a[i]);
++mid;
if(ab1<ab2)
{
ans[mid]=a[i];
ans[n-mid+1]=a[i-1];
}
else
{
ans[mid]=a[i-1];
ans[n-mid+1]=a[i];
}
}
}
else
{
int mid=n/2;
ans[mid]=a[n];
ans[n-mid+1]=a[n-1];
for(int i=n-2;i>=2;i-=2)
{
int ab1=max(ans[mid]-a[i],ans[n-mid+1]-a[i-1]);
int ab2=max(ans[mid]-a[i-1],ans[n-mid+1]-a[i]);
--mid;
if(ab1<ab2)
{
ans[mid]=a[i];
ans[n-mid+1]=a[i-1];
}
else
{
ans[mid]=a[i-1];
ans[n-mid+1]=a[i];
}
}
}
for(int i=1;i<=n;++i)
cout<<ans[i]<<" ";
return 0;
}
D. Gourmet choice（*2000）（并查集、拓扑排序）
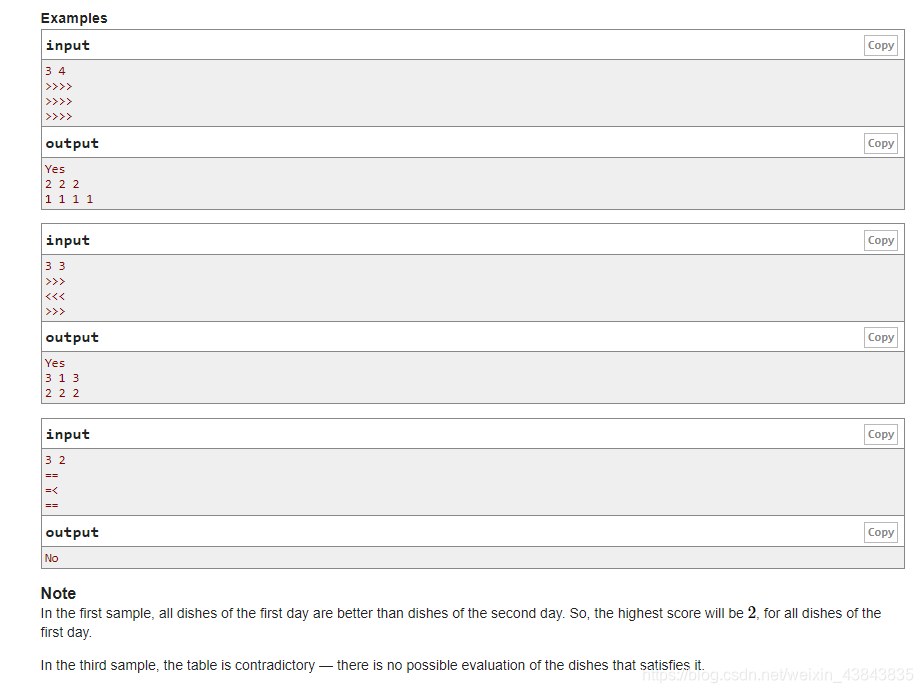
——题意——
美食家在第一天品尝了
n
n
n道菜，在第二天品尝了
m
m
m道菜，给出一张
n
∗
m
n*m
n∗m的矩阵
a
a
a，
a
[
i
]
[
j
]
a[i][j]
a[i][j]表示第一天品尝的第
i
i
i道菜和第二天品尝的第
j
j
j道菜的比较。
′
>
′
'>'
′>′表示前者比后者好，
′
<
′
'<'
′<′表示后者比前者好，
′
=
′
'='
′=′表示两者程度相同。如果能得出各个菜肴的等级，就输出
Y
e
s
Yes
Yes以及每个菜肴的等级（要求尽量小）；无法评判，则输出
N
o
No
No.
——题解——
首先可以想到，给出一些数据的大小关系，对数据进行排序，这是拓扑排序的典型特征。
其次，本题存在相等的情况，暗示用并查集进行缩点。
我们把等级低的连向等级高的，把等级相等的点用并查集关联起来，进行初次建图。
然后进行二次建图，把集合中点看做一个点，重新建立连向它的边和它连向其它点集的边。
如果此时发现，点集存在自环，则表明该集合存在两个点关系不为等号，与集合元素性质矛盾，输出
N
o
No
No
接着，我们把入度为
0
0
0的点集加入队列，进行拓扑排序，如果没有点加入，或者排序完之后仍然有点集的入度不为
0
0
0,说明存在环，输出
N
o
No
No.
当把所有点集的等级求出来后，对照着逐个输出每个点的等级。
——Code——
#include<iostream>
#include<queue>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
int n,m;
vector<int> edge[2002];
vector<int> gath[2002];
vector<int> gage[2002];
bool check[2002][2002];
bool vis[2002];
int ans[2002];
int in[2002];
int f[2002];
queue <int> q;
int find(int x)
{
if(x==f[x]) return x;
return f[x]=find(f[x]);
}
void topsort()
{
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=0;i<gage[u].size();++i)
{
int v=gage[u][i];
ans[v]=max(ans[v],ans[u]+1);
--in[v];
if(in[v]==0) q.push(v);
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n+m;++i)
f[i]=i;
for(int i=1;i<=n;++i)
{
getchar();
for(int j=1;j<=m;++j)
{
char ch;
ch=getchar();
if(ch=='>') edge[n+j].push_back(i);
if(ch=='<') edge[i].push_back(n+j);
if(ch=='=') f[find(j+n)]=f[i];
}
}
bool flag=false;
for(int i=1;i<=n+m;++i)
{
gath[find(i)].push_back(i);
vis[f[i]]=true;
}//建立点集
// for(int i=1;i<=n+m;++i)
// cout<<f[i]<<" ";
// cout<<endl;
// for(int i=1;i<=n+m;++i)
// {
// if(vis[i]==false) continue;
// cout<<"gath "<<i<<" : ";
// for(int j=0;j<gath[i].size();++j)
// cout<<gath[i][j]<<" ";
// cout<<endl;
// }//检查点集
for(int i=1;i<=n+m;++i)
{
for(int j=0;j<gath[i].size();++j)
{
int u=gath[i][j];
for(int k=0;k<edge[u].size();++k)
{
int v=find(edge[u][k]);
if(v==i)
{
flag=true;
break;
}
if(check[i][v]==false)
{
check[i][v]=true;
++in[v];
gage[i].push_back(v);
}
}
if(flag) break;
}
if(flag) break;
}//建立点集之间的边，出现自环则无解
if(flag) cout<<"No"<<endl;
else
{
// for(int i=1;i<=m+n;++i)
// {
// if(vis[i]==false) continue;
// cout<<"edge "<<i<<" : ";
// for(int j=0;j<gage[i].size();++j)
// cout<<gage[i][j]<<" ";
// cout<<endl;
// }//检查点集边
for(int i=1;i<=m+n;++i)
if(vis[i]&&in[i]==0)
{
ans[i]=1;
q.push(i);
}
if(q.empty()) cout<<"No"<<endl;
else topsort();//对点集拓扑排序
for(int i=1;i<=m+n;++i)
if(vis[i]&&in[i]!=0)
{
flag=true;
break;
}//判断是否有环
if(flag) cout<<"No"<<endl;
else
{
cout<<"Yes"<<endl;
for(int i=1;i<=n;++i)
cout<<ans[f[i]]<<" ";
cout<<endl;
for(int i=n+1;i<=m+n;++i)
cout<<ans[f[i]]<<" ";
cout<<endl;
}//输出答案
}
return 0;
}
F. Asya And Kittens（*1700）（并查集）
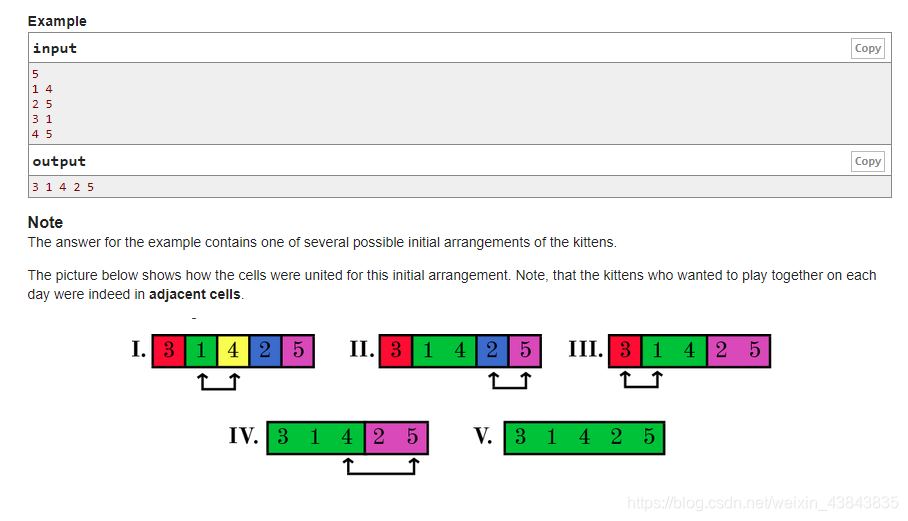
——题意——
Asya喜欢养猫，她把
n
n
n只猫放进一长排笼子里，这个笼子有
n
n
n个房间，相邻房间之间有门，即总共有
n
−
1
n-1
n−1扇门。每天Asya都会把想一起玩的猫之间的门打开。现在所有的门都被打开了，Asya不记得一开始猫是怎么排放的，只记得每天那两只猫想一起玩。要求根据Asya的回忆，推断出开始猫的排列情况。答案不唯一，输出一种可行方案。
——题解——
这题很明显是一道并查集相关的题。
每次打开一扇门，两边的猫就合并入一个集合。我们假设一开始打开的门两边的猫位于最左边且设为一个集合。以后每次读入一对编号，先查看是否与刚开始设定的集合相连，如果是的则直接把这个点所在集合加入到答案序列中，否则就把这个点的集合合并。依照这个思路，我写出了一个还算比较清晰，但明显复杂的版本，最后还是超内存了。。。
——Code——
#include<iostream>
#include<vector>
#include<cstdio>
#include<cstring>
using namespace std;
int n;
int f[150004];
int ans[150004];
vector<int> gath[150004];
int cnt;
int find(int x)
{
if(x==f[x]) return x;
return f[x]=find(f[x]);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
f[i]=i;
gath[i].push_back(i);
}
int st=-1;
for(int i=1;i<=n-1;++i)
{
int u,v;
scanf("%d %d",&u,&v);
if(st==-1)
{
++cnt;
ans[cnt]=u;
st=u;
}
if(f[find(u)]!=st&&f[find(v)]!=st)
{
for(int j=0;j<gath[f[v]].size();++j)
{
gath[f[u]].push_back(gath[f[v]][j]);
if(gath[f[v]][j]==v) continue;
f[gath[f[v]][j]]=f[u];
}
f[v]=f[u];
continue;
}
if(f[find(v)]==st)
{
int swap;
swap=u;
u=v;
v=swap;
}
for(int j=0;j<gath[f[v]].size();++j)
{
++cnt;
ans[cnt]=gath[f[v]][j];
if(gath[f[v]][j]==v) continue;
f[gath[f[v]][j]]=st;
}
f[v]=st;
}
for(int i=1;i<=n;++i)
printf("%d ",ans[i]);
return 0;
}
实际上，在进行集合合并操作时，我们只需要用集合的开头和结尾就可以了，没必要真的模拟把某个集合所有元素逐个放入另一个集合。所以，本题需要在朴素并查集上加入一个记录后驱的数组，以及一个非路径压缩的后驱数组用于输出答案。
——Code——
#include<iostream>
#include<utility>
#include<cstdio>
using namespace std;
int n;
typedef pair<int,int> pii;
pii f[150004];
int nxt[150004];
int pre(int x)
{
if(x==f[x].first) return x;
return f[x].first=pre(f[x].first);
}
int next(int x)
{
while(x==f[x].second) return x;
return f[x].second=next(f[x].second);
}
void link(int x,int y)
{
f[x].second=f[y].second;
f[y].first=f[x].first;
nxt[x]=y;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i)
f[i].first=f[i].second=i;
for(int i=1;i<=n-1;++i)
{
int u,v;
scanf("%d %d",&u,&v);
if(pre(u)!=pre(v))
link(next(u),pre(v));
}
int st=pre(n);
for(int i=st;i;i=nxt[i])
cout<<i<<" ";
return 0;
}
还有一道字符串dp和双指针是真的不会了。。。
有空再补吧，残念
扫一扫
734
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
