PTA - 建立与遍历二叉树

最新推荐文章于 2023-11-18 20:35:20 发布

Bytenerd_0

最新推荐文章于 2023-11-18 20:35:20 发布

阅读量3.6k

点赞数 8

CC 4.0 BY-SA版权

分类专栏： c++【二叉树】文章标签： c++ 数据结构二叉树

本文链接：https://blog.youkuaiyun.com/weixin_43821410/article/details/90033877

c++【二叉树】专栏收录该内容

6 篇文章

订阅专栏

本文详细介绍了如何从先序序列构建二叉树，并实现中序遍历输出。通过具体的代码示例，读者可以深入理解二叉树的链式存储结构及遍历算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

建立与遍历二叉树

题目：以字符串的形式定义一棵二叉树的先序序列，若字符是‘#’, 表示该二叉树是空树，否则该字符是相应结点的数据元素。读入相应先序序列，建立二叉链式存储结构的二叉树，然后中序遍历该二叉树并输出结点数据。

输入格式：

字符串形式的先序序列（即结点的数据类型为单个字符）

输出格式：

中序遍历结果

输入样例：

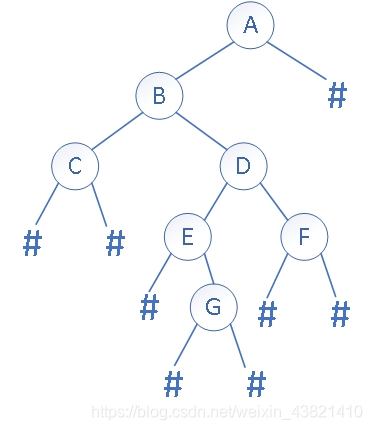
ABC##DE#G##F###

输出样例：

CBEGDFA

在这里插入图片描述

#include <iostream>

using namespace std;

struct BinaryTree_Node 
{
	char value;                // 节点的值 
	
	BinaryTree_Node* lChild;   // 左子节点 
	BinaryTree_Node* rChild;   // 右子节点 
	
	// 节点的构造函数 
	BinaryTree_Node(): lChild(NULL), rChild(NULL)
	{
	}
};

typedef BinaryTree_Node* BT_Node; 

// 创建二叉树 (先序遍历)
BT_Node Create_BinaryTree()
{
	BT_Node root = new BinaryTree_Node();
	char v;
	cin >> v;
	
	if (v != '#')
	{
		root->value = v;
		root->lChild = Create_BinaryTree();
		root->rChild = Create_BinaryTree();
	}
	
	else
		root = NULL; 
	
	return root;
}

// 中序遍历 
void In_traverse(BT_Node root)
{
	if (root == NULL)
		return;
	
	In_traverse(root->lChild);
	cout << root->value;
	In_traverse(root->rChild);
}

int main()
{
	BT_Node root;
	root = Create_BinaryTree();
	In_traverse(root);
}

小结：——二叉树知识点

2.定义结点：

2.1 二叉链表：链式存储

2.2 定义结点代码

struct BinaryTree_Node 
{
	char date;        // 节点的值 
	
	BinaryTree_Node* lChild;   // 左子节点 
	BinaryTree_Node* rChild;   // 右子节点 
	
	// 节点的构造函数 
	BinaryTree_Node(): lChild(NULL), rChild(NULL)
	{
	}
};

3.遍历（先序遍历、中序遍历、后序遍历和层次遍历）

type BinaryTree_Node* BT_Node;

//先序遍历 ————  左子树-根节点-右子树  简称：根左右
void Pre_Traverse(BT_Node root)
{
	if (root == NULL)    // 递归出口
		return;
	
	cout << root->value;
	Pre_Traverse(root->lChild);
	Pre_Traverse(root->rChild);	
}

// 中序遍历  ————  左根右
void In_Traverse(BT_Node root)
{
	if (root == NULL)    // 递归出口
		return;
	
	In_traverse(root->lChild);
	cout << root->value;
	In_traverse(root->rChild);  
 } 
 
// 后序遍历 ————  左右根
void Post_Traverse(BT_Node root)
{
	if (root == NULL)    // 递归出口
		return;
	
	Post_Traverse(root->lChild);
	Post_Traverse(root->rChild);
	cout << root->value;
}

// 层次遍历 --- 队列解法
void Level_Traverse(BT_Node root)
{
	queue<BT_Node> q;
	q.push(root);
	
	while(!q.empty())
	{
		BT_Node op = q.front();
		q.pop();
		cout << op->value;
		if (op->lChild != NULL)
			q.push(op->lChild);
			
		if (op->rChild != NULL)
			q.push(op->rChild);
		}
}

求二叉树节点的个数

// 求二叉树节点的个数
int GetNodeNum(BT_Node root)
{
	if (root == NULL)          // 递归出口 
		return 0;
	
	// 二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 根节点 
	return GetNodeNum(root->lChild) + GetNodeNum(root->rChild) + 1;  
}