暴力理解数据结构与算法2------线性表

数据结构与算法

二.数据结构与算法线性表

1.线性表概念
线性表简称表，是零个或多个元素的有穷序列，通常可以表示成K₀,k₁,…,K_n-1( n ≥ 1)

• 表目：线性表中的元素（可包含多个数据项，记录）
• 索引（下标）：i称为表目K_i的“索引”或“下标”
• 表的长度：线性表中所含元素的个数n
• 空表：长度为零的线性表（ n = 0）

线性表特点：操作灵活，其长度可以增长，缩短

线性结构

二元组B=（K,B）K={a₀,a₁,…,a_n-1} R={r}

• 有一个唯一的开始结点，它没有前驱，有一个唯一的直接后继
• 一个唯一的终止结点，它有一个唯一的直接前驱，而没有后继
• 其它的结点都叫做内部结点，每一个内部结点都有且仅有一个唯一的直接有前驱，也有一个唯一的直接有后继
• <a_i,a_i+1>a_i是a_i+1的前驱，a_i+1是a_i的后继
• 前驱/后继关系r,具有反对称性和传递性

结构特点

均匀性：虽然不同线性表的数据元素可以是各种各样的，但对于同一线性表的各数据元素必定具有相同的数据类型和长度

有序性：各数据元素在线性表中都有自己的位置，且数据元素之间的相对位置是线性的

按复杂程度划分

• 简单的：线性表，栈，队列，散列表
• 高级的：广义表，多维数组，文件…

按访问方式划分

• 直接访问型
• 顺序访问型
• 目录索引型

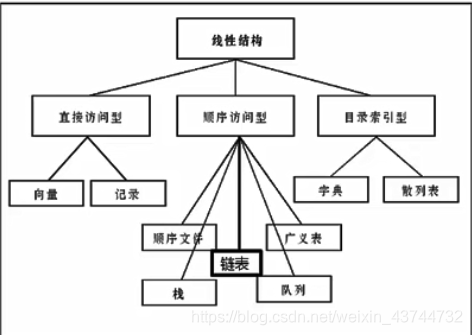
线性表逻辑结构

主要属性包括

• 线性表的长度
• 表头
• 表尾
• 当前位置

线性表

所有表目都是同一类型结点的线性表
不限制操作形式
根据存储的不同分为：1.顺序表，2.链表

顺序表

按索引值从小到大存放在一片相邻的连续区域
紧凑结构，存储密度为1

链表

单链表
双链表
循环链表

栈

插入和删除操作都限制在表的同一端进行（先进后出）

队列

插入操作在表的一端，删除操作在另一端（先进先出）

2.顺序表

也称向量，采用定长的一维数组存储结构
主要特性

• 元素的类型相同
• 元素顺序地存储在连续存储空间中，每个元素有唯一的索引值
• 使用常数作为向量长度

数组存储
读写器元素方便，通过下标即可指定位置

3.链表
通过指针把它的一串存储结点链接成一个链
存储结点由两部分组成：
数据域+指针域（后继地址）

单链表

单链表的删除
从链表中删除结点X

• 1.用p指向元素X的结点的前驱结点
• 2.删除元素为X的结点
• 3.释放X占据的空间

双链表
为弥补单链表的不足，而产生双链表

• 单链表指针域字段仅仅指向后继结点，不能有效地找到前驱，反之亦然
• 增加一个指向前驱的指针

循环链表
将单链表或者双链表的头尾结点链接起来，就是一个循环链表
不增加额外存储花销，却给不少操作带来了方便

链表边界条件

几个特殊点的处理

• 头指针处理
• 非循环链表尾结点的指针域保持为null
• 循环链表尾结点的指针回指头结点

链表处理

• 空链表的特殊处理
• 插入或删除结点时指针勾链的顺序
• 指针运动的正确性

顺序表的主要优点

• 没有使用指针，不需要花费额外开销
• 线性表元素的读访问非常简洁便利

链表的主要优点

• 无需事先了解线性表的长度
• 允许线性表的长度动态变化
• 能够适应经常插入删除内部元素的情况

总结
顺序表是存储静态数据的不二选择
链表是存储动态变化数据的良方