构造数组的MaxTree

题意描述

一个数组的MaxTree定义如下，前提是数组没有重复元素，MaxTree是一棵二叉树，数组的每一个值对应一个二叉树节点。包括MaxTree树在内且在其中的每一棵子树上，值最大的节点都是数的头节点。
对于没有重复元素的数组arr，写出生成这个数组的MaxTree的函数，要求如果 数组长度为N，则时间复杂度为O(N),额外空间复杂度为O(N)

解法1

我们可以把这个数组搞成堆，建立大跟堆的时间复杂度是O(N)。

解法2

思路
       已知数组中没有重复值，通过单调栈结构我们可以找到左边离他最近且比它大的元素，可以也可以找到右边离他最近且比他大的元素。如果一个元素没有左边最大值以及右边最大值，那么它就是头结点，如果一个数字没有左边，只有右边，或者没有右边只有左边，那么它就有唯一的父节点，那么直接挂在其父节点下(优先挂在其左边)。如果左右两边有存在比他大的，那么我们就挂在较小值节点的下面，最终得到一棵二叉树。
证明只会是二叉树，不会森林或者是多叉树
       因为我们没有重复值，只会有一个根节点，每个节点都有自己的归属。所以只会是一棵树，而不是森林。为什么不会形成多叉树，即一个节点 不会有两个以上的孩子，那么我们可以证明在某一个节点的一侧（左和右）最多只有一个节点挂在其底下。我们可以假设某一个节点一侧有两个孩子，然后我们去推矛盾。
推导

我们可以假设在元素a的右边有两个元素b和c都将会挂在a元素下面，如下图

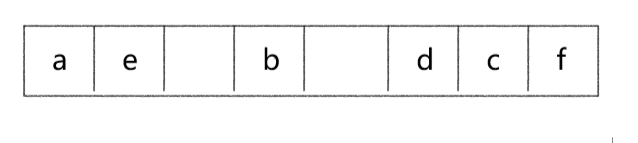
1. 如果b>c，那么c就不会挂在a上，而是直接挂在b上
2. 如果b<c，情况1：c<a，那么b会挂在c上不会挂在a上。情况2，如果c>a，那么b是会挂在a上，但是c绝对不会挂在c上，因为c>a啊。
3. 如果存在a>d>b，那么b就会直接挂在d上，而不是a上，如果d>a>b，那么b确实会挂在a上，但是由于d>a，c是不会挂在a上的，而是挂在d上。
4. 同理可以得到e和f不论取什么值，都无法让b和c同时挂在a的下面。

示例代码

#include <iostream>
#include <vector>
#include <list>
#include <stack>
#include <unordered_map>
#include <algorithm>
using namespace std;

class Node
{
public:
	Node()
		:m_value(0)
		, m_left(nullptr)
		, m_right(nullptr)
	{

	}
	Node(int value)
		:m_value(value)
		,m_left(nullptr)
		,m_right(nullptr)
	{
		
	}
	
	~Node()
	{
		cout << "destroy node " << this->m_value << endl;
		this->m_left = nullptr;
		this->m_right = nullptr;
	}
	int m_value;
	Node * m_left;
	Node * m_right;
};
// 将栈顶元素拿出，并设置到map中去
void popStackSetMap(stack<Node*> &nodeStack, unordered_map<Node *, Node *> &nodeMap)
{
	Node * top = nodeStack.top();
	nodeStack.pop();
	if (nodeStack.empty())
	{
		nodeMap.insert({ top, nullptr });
	}
	else
	{
		nodeMap.insert({ top, nodeStack.top() });
	}
}

// 由数组建立MaxTree
Node *getMaxTree(const vector<int> &arr)
{
	vector<Node *> nodeArr;
	for (int i = 0; i < arr.size(); i++)
	{
		nodeArr.push_back(new Node(arr[i]));
	}
	Node * head = nullptr;
	stack<Node*> nodeStack;
	unordered_map<Node *, Node *> lBigMap;  // 存放每个元素与其左边最近比他大的元素的指针
	unordered_map<Node *, Node *> rBigMap; // 存放每个元素与其右边最近比他大的元素的指针
	
	for (int i = 0; i != nodeArr.size(); i++)
	{
		while (!nodeStack.empty() && nodeStack.top()->m_value < nodeArr[i]->m_value)
		{
			popStackSetMap(nodeStack, lBigMap);
		}
		nodeStack.push(nodeArr[i]);
	}
	while (!nodeStack.empty())
	{
		popStackSetMap(nodeStack, lBigMap);
	}
	for (int i = nodeArr.size()-1; i != -1; i--)
	{
		while (!nodeStack.empty() && nodeStack.top()->m_value < nodeArr[i]->m_value)
		{
			popStackSetMap(nodeStack, rBigMap);
		}
		nodeStack.push(nodeArr[i]);
	}
	while (!nodeStack.empty())
	{
		popStackSetMap(nodeStack, rBigMap);
	}
	for (int i = 0; i != nodeArr.size(); i++)
	{
		Node * curNode = nodeArr[i];
		Node * left = lBigMap[curNode];
		Node * right = rBigMap[curNode];
		if (left == nullptr && right == nullptr) // 为头节点
		{
			head = curNode;
		}
		else if (left == nullptr)
		{
			if (right->m_left == nullptr)
			{
				right->m_left = curNode;
			}
			else
			{
				right->m_right = curNode;
			}
		}
		else if (right == nullptr)
		{
			if (left->m_left == nullptr)
			{
				left->m_left = curNode;
			}
			else
			{
				left->m_right = curNode;
			}
		}
		else // 左右最近的比该元素大的元素都存在，那么往值小的元素挂
		{
			Node *parent = left->m_value < right->m_value ? left : right;
			if (parent->m_left == nullptr)
			{
				parent->m_left = curNode;
			}
			else
			{
				parent->m_right = curNode;
			}
		}
	}
	return head;
}

// 先序遍历一棵树
void printPreorder(Node *head)
{
	if (head == nullptr)
	{
		return;
	}
	
	cout << head->m_value << ", ";
	printPreorder(head->m_left);
	printPreorder(head->m_right);
}
// 销毁整棵树
void destroyTree(Node *head)
{
	if (head == nullptr)
	{
		return;
	}

	destroyTree(head->m_left);
	destroyTree(head->m_right);
	delete head;
}

int main(int argc, char ** argv)
{
	vector<int> arr{ 5,2,3,6,9,4,1,7 };
	Node * head = getMaxTree(arr);
	printPreorder(head);
	destroyTree(head);
	system("pause");
	return EXIT_SUCCESS;
}