求最大子矩阵的大小

引子问题

寻找一个数组所代表的直方图中最大的长方形中包含多少个小正方形。
对于下图所示的直方图中，结果为2*5=10

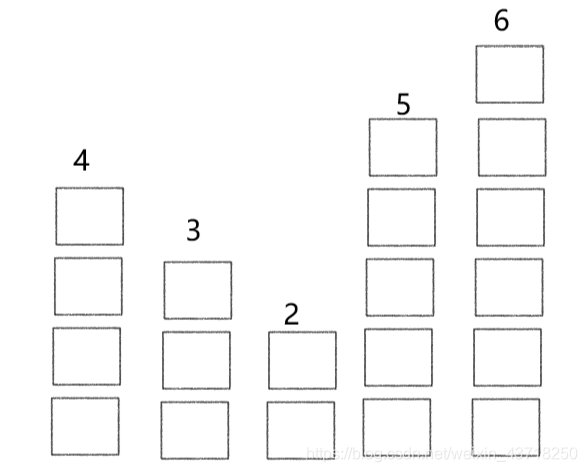
引子问题思路
       对于这个问题，我们的想法是对于直方图中每一列中最高的地方做一个标杆，然后看其向左向右分别能扩展到哪里，并记录小正方形的个数，能够出现的最大的正方形一定在这里面。具体的实现我们可以通过单调栈来完成，首先准备一个从栈底到栈顶有小到大的单调栈，我们将第一个元素压入到栈中，然后压入第二个元素的时候，判断其是否小于栈顶元素，如果大于那么就直接压入，如果小于，那么就开始结算栈顶元素为高的长方形中所有小正方形的个数。作为栈底元素，那么其可以到达的位置是0,到它自己的角标，如果没有元素加入了，但是栈中依然存在数据，那么弹出栈顶元素，栈顶元素弹出的时候，它们达到的最右边就是整个数组的最右边，而其能够达到的最左边则是栈顶下一个元素的随后一个元素。作为栈底元素，它能够到达的最左边为0。
示例代码

#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
using namespace std;

int maxRecFromBottom(vector<int> height)
{
	if (height.size() < 1)
	{
		return 0;
	}
	int maxArea = 0;
	stack<int> intStack;
	for (int i = 0; i < height.size(); i++)
	{
		//如果栈为空或者当前值所代表的的数组元素大于栈顶的值所代表的的数组元素, 直接跳出来
		while (!intStack.empty() && height[i] < height[intStack.top()])
		{
			int j = intStack.top();
			intStack.pop();
			int k = intStack.empty() ? -1 : intStack.top();
			int curArea = (j - k - 1)*height[j];
			maxArea = max(maxArea, curArea);
		}
		intStack.push(i);
	}
	// 对于剩余元素我们全部弹出
	while (!intStack.empty())
	{
		int j = intStack.top();
		intStack.pop();
		int k = intStack.empty() ? -1 : intStack.top();
		int curArea = (height.size() - k - 1)*height[j];
		maxArea = max(maxArea, curArea);
	}
	return maxArea;
}

int main(int argc, char ** argv)
{
	vector<int> arr{ 4,3,2,5,6 };
	int res = maxRecFromBottom(arr);
	cout << res << endl;
	system("pause");
	return EXIT_SUCCESS;
}

主干问题

给定一个整形矩阵Map，其中的值只有0和1量中，求其中全是1的所有矩形区域中，最大的矩形区域为1的数量。

思路
对于上面的大问题，我们可以计算以每一行为底的情况下，我们可以使用引子问题中的解法找到该数组[1,0,1,1]所能够产生的最大的矩形。我们可以从第0行到最后一行都使用引子问题中的方法找到该行中最大的长方形中所包含小正方形的个数。注意，当我们对下一行使用以上方法的时候，我们需要对该行数据进行处理，如果某个元素为0，那么保持不变，如果为1，那么就加上前一列中对应位置上的元素。如果N为矩阵行数，M为矩阵列数，那么时间复杂度是O(N*M)的。

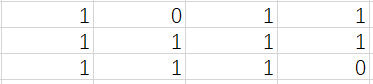
比如对于上图中的矩阵，我们可以使用引子问题中的函数解决第一行为底的数组的最大值问题，结果为2。当以第二行为底时，结果为4，当以第三行为底时，结果为6。
示例代码

int maxRectSize(vector<vector<int>> &matrix)
{
	if (matrix.size() == 0 || matrix[0].size() == 0)
	{
		return 0;
	}
	int maxArea = 0;
	vector<int> height(matrix[0].size(),0);
	for (int i = 0; i < matrix.size(); ++i)
	{
		for (int j = 0; j < matrix[0].size(); ++j)
		{
			int tar = matrix[i][j] == 0 ? 0 : height[j] + 1;
			height.push_back(tar);
		}
		maxArea = max(maxArea, maxRecFromBottom(height));
	}
	return maxArea;
}