Dijkstra算法

主要思想

设置一个集合S存放已经找到最短路径的顶点，S的初始状态只包含源点v，
对vi∈V - S，假设从源点v到vi的有向边为最短路径（从v到其余顶点的最短路径的初值）。
以后每求得一条最短路径v, …, vk，就将vk加入集合S中，并将路径v, …, vk, vi与原来的假设相比较，取路径长度较小者为最短路径。
重复上述过程，直到集合V中全部顶点加入到集合S中

列题

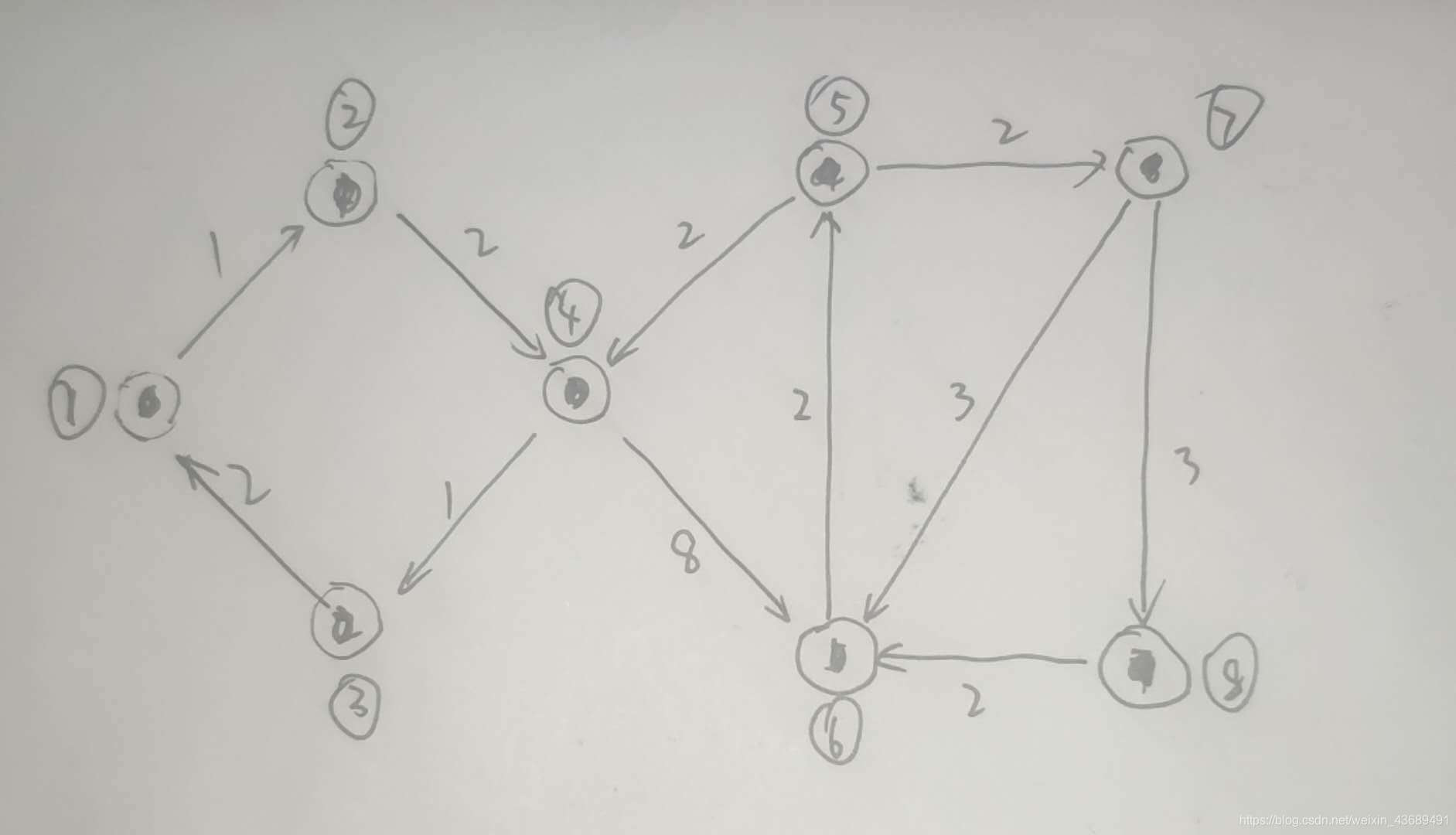
#include <bits/stdc++.h>
#define Inf 1000000
using namespace std;
int MAP[1005][1005]; 
int vis[1005], dis[1005];
int n, m;//n个点，m条边
void Init() //原地到原地边权为0
{
	memset(MAP, Inf, sizeof(MAP));
 	for (int i = 1; i <= n; i++)
 	{
 		MAP[i][i] = 0;
 	}
 }
 void Getmap() //输入数据
{
	int u, v, w;
 	for (int t = 1; t <= m; t++)
 	{
  		cin >> u >> v >> w;
  		if (MAP[u][v] > w)
  		{
   			MAP[u][v] = w;
 		 }
 	}
}
void Dijkstra(int u){//起点为u
	memset(vis, 0, sizeof(vis)); //全部为0，都没有确定
	for (int t = 1; t <= n; t++) 	
	{
 		dis[t] = MAP[u][t]; 
	}
 	vis[u] = 1;
 	for(int t=1;t<=n;t++){
 		if(!vis[i]&&dis[i]<minn){
 			minn=dis[i];
 			temp=i;
 		}
 	}
 	vis[temp]=1;
 	for(int i=1;i<=n;i++){
 		if(MAP[temp][i]+dis[temp]<dis[i])
 			dis[i]=MAP[temp][i]+dis[temp];
 	}

}
int main(){
	cin>>m>>n;
	Init();
	Getmap();
	Dijkstra(1);//起点为1端点
	cout<<dis[8];//1到8的最短距离

结果