提出一种新型深度网络结构——公路网络，该结构能有效解决深层网络训练难题。通过自适应门控机制，实现信息沿网络各层间的高效流通。即使数百层的网络亦可通过简单梯度下降完成训练。
Training Very Deep Network（Hightway Network）
文章目录
摘要
理论和经验都证明神经网络的深度对其成功来说至关重要。
但是深度越深，训练难度越大，这是一个开放性问题。为决解此问题，作者设计了一种新的网络结构，称为“公路”。
这种公路网络可以使得畅通无阻的信息流跨过“公路”的很多层。
它们是受长短期记忆循环网络启发，使用自适应门控制单元来调节信息流。
即使是几百层的公路网也能通过简单的梯度下降进行训练。这使得我们可以研究深且有效的网络。
1. 介绍&之前的工作
-
介绍了网络深度的重要性，举例说明之前的很多成功模型案例都强调了其深度。
-
介绍了为了解决训练深度网络困难的问题，之前做了哪些工作。
- 开发更好的优化器
- 设计更好的初始化层策略
- 某些基于局部竞争的激活函数
- 跳跃连接
- 蒸馏
- 分层训练
-
指出训练深度网络仍然存在问题，传统的前馈网络结构中多个非线性变化叠加在一起经常导致激活函数和梯度传播的效果不好。所以仍需继续研究
-
作者提出了自己的方法，受启发于长短期循环记忆网络（LSTM），作者提出调整深度前馈网络的结构来使层与层之间的信息流动更加容易。
通过一种自适应的门机制来实现，这种机制允许计算路径，信息沿着计算路径穿越很多层而不会衰减。作者将这种路径称为“信息公路”，他们产生了公路网络。
-
本文最基础的贡献是展示了极其深的网络也可以用 S G D SGD SGD直接进行训练，计算预算有限的深度网络如果转换成公路网络能够直接在一个阶段内被训练（[25]中提到需要两个训练阶段）。
-
实现结果证明了训练的容易，以及公路网络同样对 未预见的数据有良好的泛化能力。
2. 公路网络
约定粗体字母代表向量和矩阵，斜体大写字母代表变换方程。 σ ( x ) = 1 1 + e − x , x ∈ R \sigma(x)= \frac{1}{1+e^{-x}},x \in R σ(x)=1+e−x1,x∈R，点（·）代表点乘。
普通的前馈神经网络由 L L L层组成，对每一层的输入 x x x施加非线性变换，表示为
y = H ( x , W H ) y=H(x,W_H) y=H(x,WH) （1）
H H H一般代表仿射变换，其后跟随者非线性激活函数，但它也可能采取其他的形式，卷积或者循环等。
耽于公路网络来说，作者额外定义了两个非线形变换 T ( x , W T ) 和 C ( x , W C ) T(x,W_T)和C(x,W_C) T(x,WT)和C(x,WC)：
y = H ( x , W H ) ⋅ T ( x , W T ) + x ⋅ C ( x , W C ) y=H(x,W_H)·T(x,W_T)+x·C(x,W_C) y=H(x,WH)⋅T(x,WT)+x⋅C(x,WC) (2)
作者将 T T T定义为 t r a n s f o r m g a t e transform\space gate transform gate， C C C定义为 c a r r y g a t e carry\space gate carry gate。因为他们分别表示输出有多少是通过转换输入产生的，有多少是直接由输入产生的。
简单起见，本文设 C = 1 − T C=1-T C=1−T，有
y = H ( x , W H ) ⋅ T ( x , W T ) + x ⋅ ( 1 − T ( x , W T ) ) y=H(x,W_H)·T(x,W_T)+x·(1-T(x,W_T)) y=H(x,WH)⋅T(x,WT)+x⋅(1−T(x,WT)) (3)
x , y , H ( x , W H ) , T ( x , W T ) x,y,H(x,W_H),T(x,W_T) x,y,H(x,WH),T(x,WT)的维度必须相同。
观察T的几个特殊值：
(4)
所以当 T = 0 T=0 T=0时， y y y 的信息全部来自于x，当 T = 1 T=1 T=1时， y y y和普通的卷积函数没有区别。故可以根据 T T T这个所谓的门函数来调整输出信息中原始的输入信息和转换信息所占的比例。
个人理解
从理解上来讲达到类似于“残差函数”的效果，但其灵活性又要比残差网络高的多，残差模块中在跳跃连接层（即包含前面某层输入的层）对应着 H ( x ) = x + F ( x ) H(x)=x+F(x) H(x)=x+F(x)，而跳跃连接所跳跃的层（即不含前面层的输入的层）对应着 H ( x ) = F ( x ) H(x)=F(x) H(x)=F(x)。
可以看出，残差模块与本文的 h i g h w a y highway highway 层相比的优点在于，没有多余的参数，不用因为要进行T变换而学习额外的 W T W_T WT，而缺点在于无法调整结果中来自原始输入的信息和来自转换后信息的比例，不够灵活。
变换层的雅可比矩阵：
(5)
因此，取决于变换门机制的输出，公路层可以在 H H H和传递进来的输入 x x x之间平滑的变化。就好像一个普通的，由多个计算单元组成的层一样，其中第 i i i个单元计算 y i = H i ( x ) y_i=H_i(x) yi=Hi(x)
公路网由很多个块组成，第 i i i块计算块状态 H i ( x ) H_i(x) Hi(x)和 t r a n s f o r m g a t e transform\space gate transform gate的输出 T i ( x ) T_i(x) Ti(x)，最终产生块输出；
y i = H i ( x ) ⋅ T i ( x ) + x i ⋅ ( 1 − T i ( x ) ) y_i=H_i(x)·T_i(x)+x_i·(1-T_i(x)) yi=Hi(x)⋅Ti(x)+xi⋅(1−Ti(x))，这个块输出连接到下一层
2.1 构建公路网络
式（ 3 ） 式（3） 式（3）需要 x , y , H ( x , W H ) , T ( x , W T ) x,y,H(x,W_H),T(x,W_T) x,y,H(x,WH),T(x,WT)的维度必须相同。为了改变中间表征的尺寸，可以通过：
- 对 x x x下采样或者 0 0 0填充获得的 x ^ \hat x x^来代替 x x x
- 用普通卷积层来改变维度大小（本文所采用的策略）
2.2 训练深度公路网络
定义 t r a n s f o r m g a t e transform\space gate transform gate为 T ( x ) = σ ( W T T x + b T ) T(x)=\sigma(W_{T}^Tx+b_T) T(x)=σ(WTTx+bT)，其中 W T W_T WT为权重矩阵 b T b_T bT为截距向量。
介绍了具体的初始化方法，初始值的设定。
3. 实验
训练方法：
- SGD with momentum
- 指数衰减的learning rate
- 所有卷积公路网络都使用 R e L U ReLU ReLU来计算块状态 H H H
- 实验通过 C a f f e Caffe Caffe和 b r a i n s t o r m brainstorm brainstorm完成
3.1 优化
作者在MINIST数据集上训练了不同深度的普通网络和公路网络。
-
所有网络的很瘦小：公路网每层 50 50 50块，普通网络每层 71 71 71个计算单元，每层具有基本相同的参数数量（大约 5000 5000 5000个）。
-
所有的网络第一层都是全连接层，后面是9、19、49、或者99全连接层或者公路层。
-
最后，网络的输出通过 s o f t m a x softmax softmax产生。
作者对每个网络进行了100次运行来寻找好的超参数，包括初识学习率、动量、学习指数衰减因子和激活函数。
对于公路网络来说，有一个额外的超参数，即 t r a n s f o r m g a t e transform\space gate transform gate的池数值截距（-1～-10）之间。
每个深度性能最好的网络的训练曲线，如下图所示：
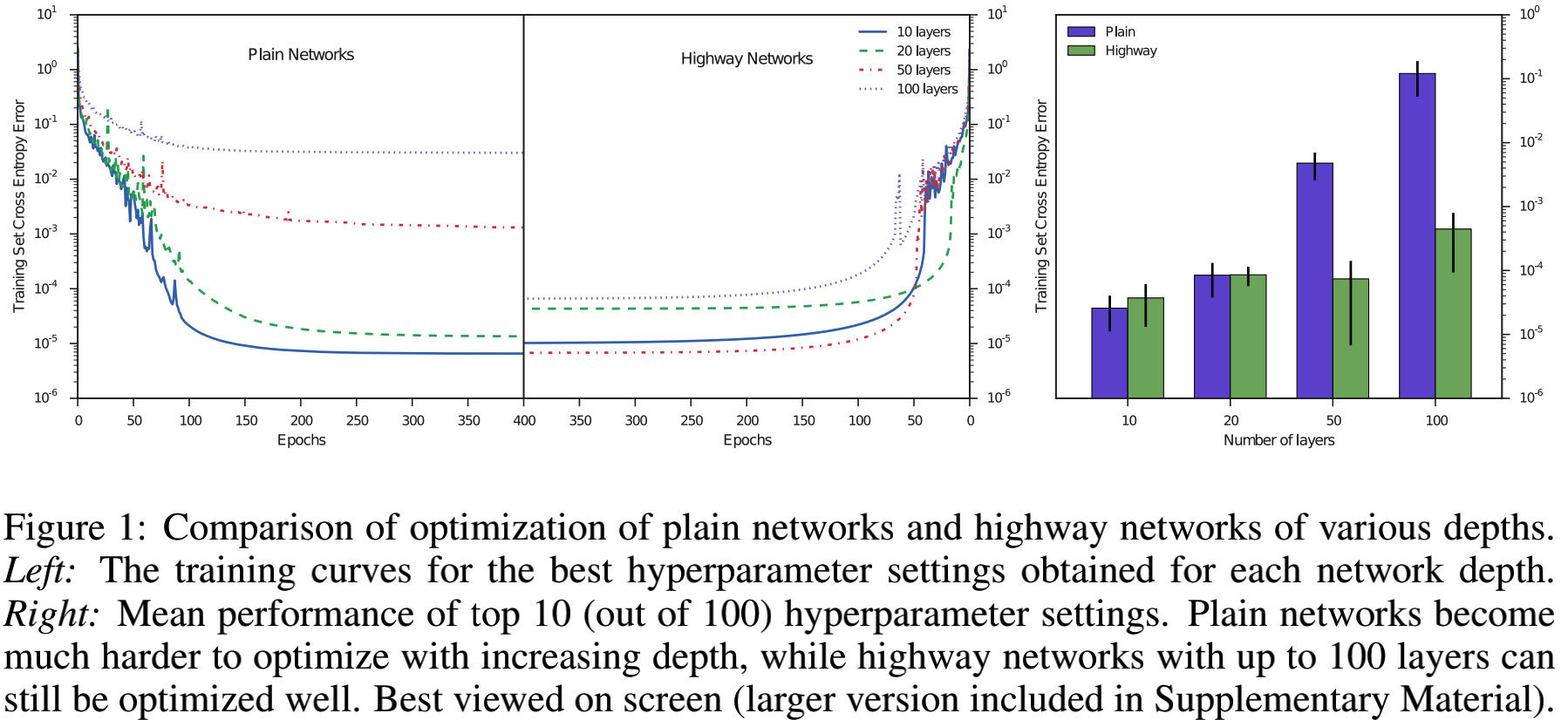
3.2 M I N I S T MINIST MINIST
效果一样，但参数更少
3.3 C I F A R − 10 和 C I F A R − 100 CIFAR-10和CIFAR-100 CIFAR−10和CIFAR−100
3.3.1 与 F i t n e t s Fitnets Fitnets对比
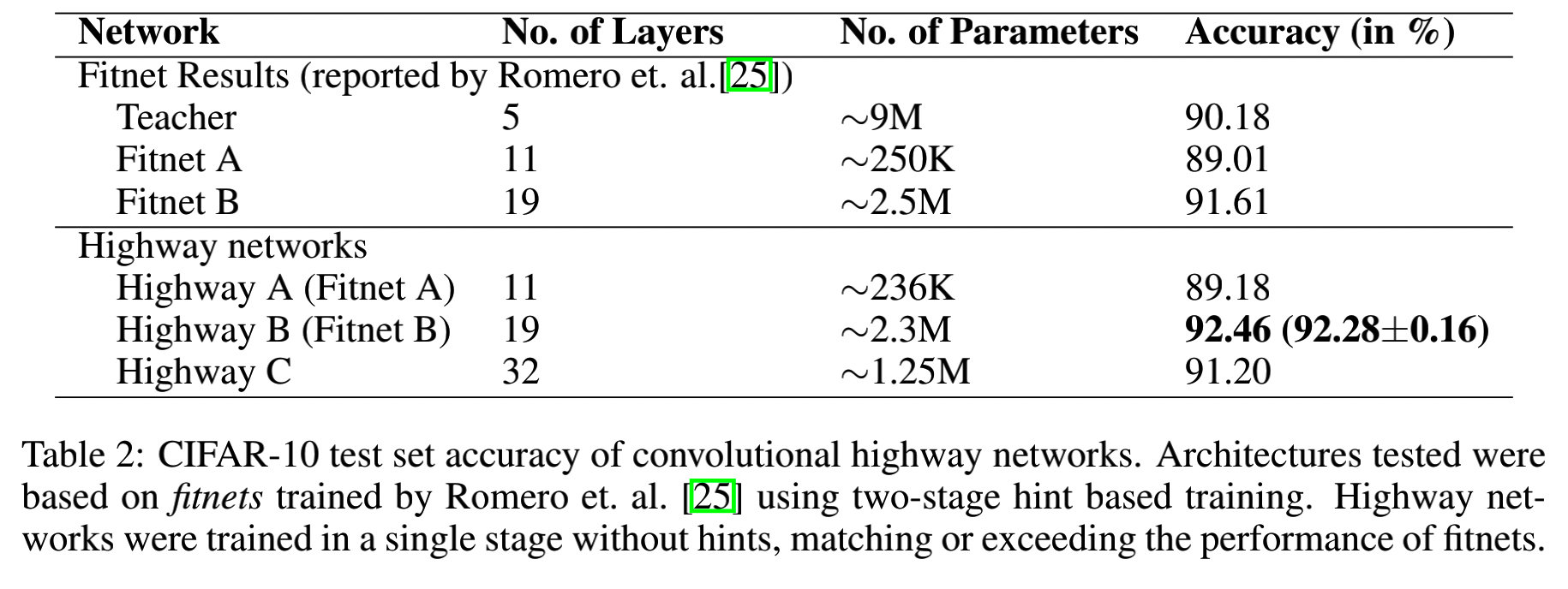
3.3.2 与先进方法对比
扫一扫
341
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
