模块1 随机过程
随机过程与样本函数
随机过程指一类随时间做随机变化的过程,用ξ(t)表示,其值不确定,无法用确切的时间函数描述。
随机过程的每一次实现,就称为一次样本函数ξi(t),随机过程是所有样本函数的集合。
基于样本函数,随机过程亦可看作是在时间进程中,处于不同时刻的随机变量的集合。

随机过程的研究需要借助统计特征与数字特征。
随机过程的统计特征
在任意一个确定时刻t1上ξ(t1)是⼀一个随机变量,这一随机变量分布函数表示为:
F1(x1, t1) = P[ξ(t1) ≤ x1]
其中x1称为门限,t1称为时间,P表示概率。
这一随机变量量的概率密度函数表示为:f1(x1, t1) =∂F(x1, t1)/ ∂x1
对于多个确定时刻t1, t2,…tn,
分布函数表示为:Fn(x1, x2 . . . xn; t1, t2 . . . tn) = P[ξ(t1) ≤ x1, ξ(t2) ≤ x2 . . . ξ(tn) ≤ xn]
概率密度函数表示为:fn =∂nFn(x1, x2 . . . xn; t1, t2 . . . tn)/ ∂x1∂x2 . . . ∂xn
随机过程的数字特征
期望: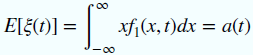
方差: 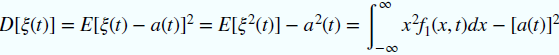
自相关:用于衡量同一过程的不同时间的相关程度 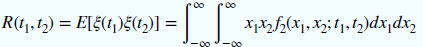
互相关:自相关概念的延伸,用于衡量两个或多个随机过程在不同时间的相关程度。 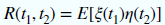









 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 2085
2085

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








