保研面试/考研复试高等数学问题整理

1. 五种基本初等函数

指数函数、对数函数、幂函数、三角函数、反三角函数

2. 函数零点怎么求

① 解方程：通过解方程$f(x)=0$得到零点。

② 数形结合：转化成两个函数图像的交点问题。

③ 利用零点存在定理和函数单调性。

零点存在定理：如果函数$y=f(x)$在区间$[a,b]$上的图象是连续不断的一条曲线，并且有$f(a)\cdot f(b)<0$，那么，函数$y=f(x)$在区间$(a,b)$内有零点，即至少存在一个$c\in (a,b)$，使得$f(c)=0$，这个$c$也就是方程$f(x)=0$的根。

④ 二分法

⑤ 牛顿迭代法

牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x)=0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。

3. 函数极限和数列极限

1) 函数极限

2) 数列极限

4. 连续、可（偏）导、可微

1) 连续与可导

a) 连续：左极限等于右极限等于函数值，即 $\underset{x\to x_0}{\lim }f(x)=f(x_0)$。

其定义如下：设函数$y=f(x)$在点$x_0$的某一邻域内有定义，如果函数$f(x)$当$x\to x_0$时的极限存在，且$\underset{x\to x_0}{\lim }f(x)=f(x_0)$,则称函数$y=f(x)$在点$x_0$处连续。

b) 可导：$\underset{\Delta x\to 0}{\lim }$$\frac{f(x_0+\Delta x)-f(x_0)}{△x}$存在，则$y=f(x)$ 在点$x_0$处可导。

函数在一点的导数是因变量在点$x_0$处的变化率，它反映了因变量随自变量的变化而变化的快慢程度。

2) 可导与可微

• 一元函数中可导与可微等价。 $dy=A\Delta x=f^{\prime }(x_0)\Delta x$
• 对于多元函数，$dz=f_x(x,y)dx+f_y(x,y)dy$
• 导数的几何意义——切线的斜率- 微分的几何意义——切线纵坐标的增量

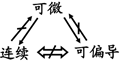
3) 多元函数连续、可（偏）导、可微的关系

5. 什么是解析？什么是奇点？

1) 解析

函数在某点处解析指函数在该点及其领邻域内处处可导。（如果一个函数$f(x)$不仅在某点$x_0$处可导，而且在$x_0$点的某个邻域内的任一点都可导，则称函数$f(x)$在$x_0$点解析。）如果函数$f(x)$在区域$D$内任一点解析，则称函数$f(x)$在区域$D$内解析，用$X$来表示$Y$的某种函数关系，称为该函数的解析式。

• 函数的解析

注意：

1. 函数f(x)在区域D内解析与在区域D内可导是等价的。
2. 函数f(x)在某一点处解析与在该点处可导是不等价的。函数在某点解析意味着函数在该点及其某个邻域内处处可导；而函数在某点可导，在该点邻域内函数可能解析，也可能不解析。
3. 解析函数的导数仍然是解析的。

2) 奇点

未定义的点。 如函数 $f(x)=1/x$在$x=0$ 的点，是一个奇点。

6. 微分中值定理

1) 费马引理

2) 罗尔中值定理

3) 拉格朗日中值定理

拉格朗日中值定理，也简称中值定理，是罗尔中值定理的更一般的形式，同时也是柯西中值定理的特殊情形。

4) 柯西中值定理

5) 三个微分中值定理的关系

拉格朗日中值定理是罗尔中值定理的推广、柯西中值定理是拉格尔朗日中值定理的推广。

7. 泰勒公式（泰勒展开）

1) 概述

泰勒公式的初衷是用多项式来近似表示函数在某点周围的情况。

泰勒公式，是一个用函数在某点的信息描述其附近取值的公式。 如果函数满足一定的条件，泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。

2) 泰勒中值定理（泰勒公式）

3) 常见余项

[1] 皮亚诺余项：$R_n(x)=o([(x-x_0){]}^n)$，这里只需要$n$阶导数存在。
[2] 拉格朗日余项：$R_n(x)=\frac{f^{(n+1)}}{(n+1)!}(x-x_0{)}^{(n+1)}$，其中$\theta \in (x_0,x)$.

4) 麦克劳林公式

5) 几何意义

泰勒公式的几何意义是利用多项式函数来逼近原函数，由于多项式函数可以任意次求导，易于计算，且便于求解极值或者判断函数的性质，因此可以通过泰勒公式获取函数的信息，同时，对于这种近似，必须提供误差分析，来提供近似的可靠性。

8. 函数的凹凸性

1) 驻点：一阶导数为 $0$ 的点；拐点：二阶导数为 $0$ 的点。

2) 凸函数和凹函数

• 凸函数：$f(\frac{x_1+x_2}{2})⩽\frac{f(x_1)+f(x_2)}{2}$，$x_1$、$x_2$ 为区间上任意两点，开区间上满足二阶导数恒大于等于 $0$。证明：通过拉格朗日中值定理。

• 凹函数：与凸函数相反。

9. 积分

1) 积分定理

2) （定）积分中值定理

3) 微积分基本公式（牛顿——莱布尼兹公式）

微积分基本公式表明：

4) 定积分如何求（换元积分法、分部积分法）

5) 不定积分的几何意义

6) 定积分的几何意义

7) 二重积分的几何意义

8) 黎曼积分

[1] 黎曼和

[2] 黎曼积分

对于一个函数$f$，如果在闭区间$[a,b]$上，无论怎样进行取样分割，只要它的子区间长度最大值足够小，函数$f$的黎曼和都会趋向于一个确定的值$S$，那么$f$在闭区间$[a,b]$上的黎曼积分存在，并且定义为黎曼和的极限$S$。这时候称函数$f$为黎曼可积的。将$f$在闭区间$[a,b]$上的黎曼积分记作：${\int }_a^{b}f(x)dx$

10. 向量的内积、外积、混合积

1) 内积(数量积/点乘/点积)：得到的是一个数

2) 外积(向量积/叉乘/叉积)：得到的是一个向量

3) 混合积：得到的是一个数

11. 场论中的梯度、散度、旋度

1) 方向导数与梯度（数量场）

[1] 方向导数

方向导数：在函数定义域内的点，对某一方向求导得到的导数。

方向导数：在某一个点 处沿方向l，函数对距离的变化率。

[2] 梯度：一个向量

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。 比如函数$f(x,y)$, 分别对$x,y$求偏导数，求得的梯度向量就是$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}{)}^T$,简称$gradf(x,y)$或者$\nabla f(x,y)$。对于在点$(x_0,y_0)$的具体梯度向量就是$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial y_0}{)}^T$.或者$\nabla f(x_0,y_0)$，如果是3个参数的向量梯度，就是$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}{)}^T$,以此类推。

梯度向量的几何意义：函数变化增加最快的地方。沿着梯度向量的方向，更容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，更容易找到函数的最小值。

2) 散度：一个数，对应内积

散度（divergence）可用于表征空间各点矢量场发散的强弱程度，物理上，散度的意义是场的有源性。当 $divF>0$，表示该点有散发通量的正源（发散源）；当 $divF<0$ 表示该点有吸收通量的负源（洞或汇）；当 $divF=0$，表示该点无源。

3) 旋度：一个向量，对应外积

旋度是向量分析中的一个向量算子，可以表示三维向量场对某一点附近的微元造成的旋转程度。这个向量提供了向量场在这一点的旋转性质。旋度向量的方向表示向量场在这一点附近旋转度最大的环量的旋转轴，它和向量旋转的方向满足右手定则。旋度向量的大小则是绕着这个旋转轴旋转的环量与旋转路径围成的面元的面积之比。

4) 散度与旋度

12. 各类级数

13. 欧拉公式

14. 傅里叶级数（傅里叶展开）

1) 傅里叶展开

2) 意义

任意周期信号可以通过傅里叶展开分解为直流分量和一组不同幅值、频率、相位的正弦波，即用三角函数之和近似表示复杂的周期函数。

3) 傅里叶变换

傅里叶变换是一种线性积分变换，用于信号在时域（或空域）和频域之间的变换。

傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。

傅里叶变换认为一个周期函数(信号)包含多个频率分量，任意函数（信号）$f(t)$ 可通过多个周期函数（基函数）相加而合成。

从物理角度理解傅里叶变换是以一组特殊的函数（三角函数）为正交基，对原函数进行线性变换，物理意义便是原函数在各组基函数的投影。

4) 傅里叶级数和傅里叶变换的关系

傅里叶级数仅适用于周期信号，傅里叶变换可以视作傅里叶级数的延伸，可以用于分析非周期信号的频谱特性。

周期信号才有傅里叶级数，非周期信号才有傅里叶变换，傅里叶变换是由傅里叶级数将周期拓展到无穷而证明来的，傅里叶级数是对应谐波的幅度，而傅里叶变换是一个谱密度的概念。