第五节——softmax回归

softmax回归

回归和分类的区别

回归估计一个连续值，分类预测一个离散类别。

回归——

单连续数值输出
自然区间R
跟真实值的区别作为损失

分类——

通常多个输出
输出i是预测为第i类的置信度

从回归的单输出，变为多个输出，输出的个数为类别个数。

从回归过渡到分类——以猫狗鸡图片分类为例

数据准备：

该例子中，每次输入都是2x2的灰度图像，每个像素对应一个标量，每个图像对应四个特征$x_1,x_2,x_3,x_4$。每个图像属于类别“猫、狗、鸡”中任一个。

在线性回归模型中，我们期望得到的输出只有一个，而分类需要所有可能类别的条件概率，即需要有多个输出，每个类别对应一个输出。我们需要进行的操作为：

首先，对类别进行独热编码(one-hot encoding)。独热编码是一个向量，它的分量和类别一样多。类别对应的分量设置为1，其他所有分量设置为0。类别可能是数、字符串等。如下所示。

$y=[y_1,y_2,...,y_n{]}^T$

y i = { 0 ， o t h e r w i s e 1 ， i f i = y y_i=\{^{1，ifi=y}_{0，otherwise} yi​={0，otherwise1，ifi=y​

本例中，$y$的取值范围为 { ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) } \{(1,0,0),(0,1,0),(0,0,1)\} {(1,0,0),(0,1,0),(0,0,1)}。

网络结构

我们需要和输出一样多的仿射函数(afine function)，每个输出对应于自己的仿射函数。该例子中，我们有4个特征和3个可能的输出类别，我们将需要12个标量来表示权重(带下标的w)，3个标量表示偏置(带下标的b)，可以得到每个输入未归一化的预测：$o_1、o_2、o_3$。
神经网络表示如图：
是一个单层神经网络，由于计算每个输出都取决于所有输入，所以输出层也是全连接层。

输出匹配概率

我们期望模型的输出可以视为属于对应类别的概率，然后可以选择具有最大输出值的类别作为我们的预测：

$y^{\ast }=argma{x}_i{o}_i$

但未归一化的输出，与概率存在一些差距——首先，没有限制它们的总和为1，且根据输入的不同，有可能为负值。

解决问题——softmax函数
为了将未归一化的预测变换为非负并且总和为1，同时要求模型保持可导。我们首先对每个未归一化的预测求幂，这样可以确保输出非负。为了确保最终输出的总和为1，我们再对每个求幂后的结果除以它们的总和。如下式：

softmax运算不会改变未归一化的预测o之间的顺序，只会确定分配给每个类别的概率。因此，在预测过程中，我们仍然可以用下式来选择最有可能的类别。

尽管softmax函数是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定，因此softmax回归是一个线性模型。

损失函数——交叉熵损失

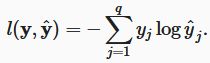
由于y是一个长度为q的独热编码向量，所以除了一个项以外的所有项j都消失了。由于所有y^j都是预测的概率，所以它们的对数永远不会大于0。
将softmax函数代入其中，得到如下：
相对于任何未归一化的预测$o_j$的导数，得到梯度——
即导数是我们模型分配的概率（由softmax得到）与实际发生的情况（由独热标签向量表示）之间的差异。

模型预测和评估

使用准确率来评估模型的性能。准确率等于正确预测数与预测的总数之间的比率。