思路分析:
-
堆排序主要是使用了堆的性质,进行排序操作,主要有两种方式
1)非原地排序:将给定数据,放入大顶堆中,然后不断取出堆的最大元素,直到堆为空。取出数据的顺序,就是待排序数据的降序(此方法需要创建额外的空间,用以存放取出的数据,所以空间复杂度为O(N))。
2)原地排序(常用):使用堆的元素下沉思想,在给定空间进行原地排序
a、给定任意待排序的数组可以看作是是一颗二叉树。
b、然后将此二叉树转换为一个大顶堆。
c、最后依次将大顶堆的最大元素放在指定位置(去掉最大元素后,堆最后一个元素坐标的下一个坐标)。
3)将给定数组转换为大顶堆(主要利用堆元素的下沉操作)
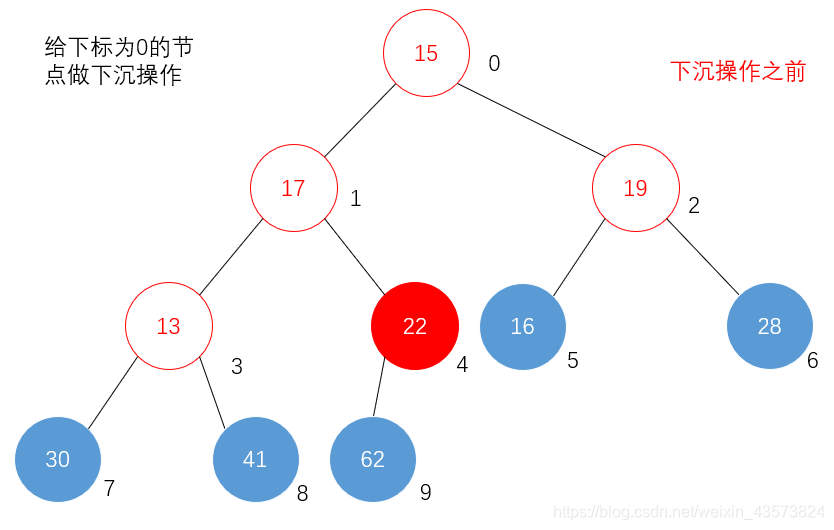
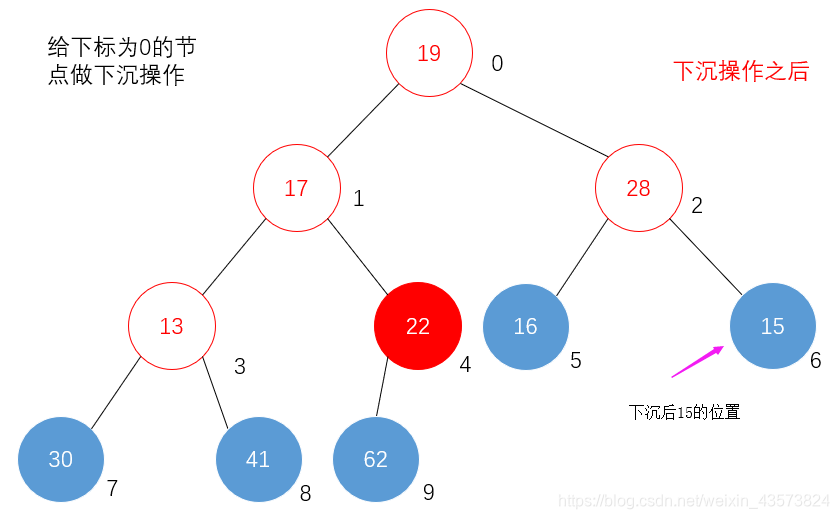
a、从堆的最后一个非叶子节点开始,依次往前,做下沉操作,直到下标为0;
b、具体下沉操作:若当前节点元素比较大的一个子节点的值要小,就需要将当前节点的值与较大节点的值做交换。然后将值较大的节点作为当前节点,继续做判断。直到当前节点为叶子节为止。
时间复杂度
- 堆排序较为稳定,最坏、最好、平均时间复杂度都为:O(nlog2n)(以2为底,n的对数,乘以n)
空间复杂度
- O(1)
代码实现:
public class Sort {
/**
* 堆排序
* @param arr 待排序数组
*/
public static void heapSort(int[] arr) {
long start = System.currentTimeMillis();
int n = arr.length;
if (n <= 1) {
return;
}
// 将给定数组变为大顶堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
siftDown(arr,n,i);
}
//将大顶堆的最大元素取出,放在最终位置
for (int i = n - 1; i >= 0; i--) {
swap(arr,i,0);
siftDown(arr,i,0);
}
long end = System.currentTimeMillis();
System.out.println("堆排序用时:" + (end - start) + "毫秒");
}
/**
* 将给定下标的元素移动到正确的位置(元素下沉)
* @param arr 给定数组
* @param n 给定数组的长度
* @param index 待移动元素的下标
*/
private static void siftDown(int[] arr, int n, int index) {
while (index * 2 + 1 < n) { //判断当前节点是否为最后一个非叶子节点
int i = index * 2 + 1;
if (i + 1 < n) { //判断当前节点是否存在右子树
if (arr[i] < arr[i+1]) {
i++;
}
}
//判断当前节点的值是否小于较大节点的值
if (arr[index] > arr[i]) {
return;
}
swap(arr,index,i);
index = i;
}
}
/**
* 交换给定数组中指定下标的两个元素
* @param arr 给定数组
* @param i 待交换元素1
* @param j 待交换元素2
*/
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
一千万个随机数字测试,堆排序用时:3411毫秒左右
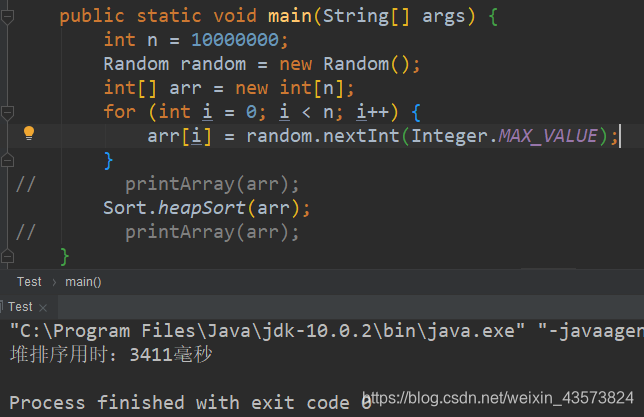





 堆排序是一种基于比较的排序算法,通过构建大顶堆并不断调整堆来达到排序的目的。文章详细介绍了堆排序的非原地和原地排序两种方法,并讲解了如何将数组转换为大顶堆的过程。在时间复杂度上,堆排序稳定在O(nlog2n),而空间复杂度仅为O(1)。在实际测试中,堆排序在一千万个随机数字上的运行时间为3411毫秒。
堆排序是一种基于比较的排序算法,通过构建大顶堆并不断调整堆来达到排序的目的。文章详细介绍了堆排序的非原地和原地排序两种方法,并讲解了如何将数组转换为大顶堆的过程。在时间复杂度上,堆排序稳定在O(nlog2n),而空间复杂度仅为O(1)。在实际测试中,堆排序在一千万个随机数字上的运行时间为3411毫秒。
















 30万+
30万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








