树：构建BST，返回个数/序列

给定一个值n，能构建出多少不同的值包含1...n的二叉搜索树（BST）？

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

 

示例:

 

输入: 3

输出: 5

解释:

给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

 

   1         3     3      2      1

    \       /     /      / \      \

     3     2     1      1   3      2

    /     /       \                 \

   2     1         2                 3

 

解题思路：

1.给定一个有序序列 1 ... n，为了根据序列构建一棵二叉搜索树。我们可以遍历每个数字 i，将该数字作为树根，1 ... (i-1) 序列将成为左子树，(i+1) ... n 序列将成为右子树，递归地从子序列构建子树。

2.不同的二叉搜索树的总数 G(n)G(n)G(n)，是对遍历所有 i (1 <= i <= n) 的 F(i,n)F(i, n)F(i,n) 之和。

 

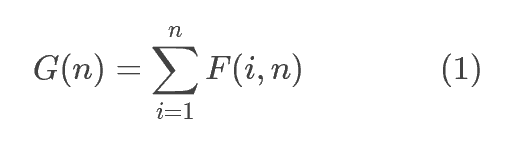
3.给定序列 1 ... n，我们选出数字 i 作为根，则对于根 i 的不同二叉搜索树数量 F(i,n)，是左右子树个数的笛卡尔积

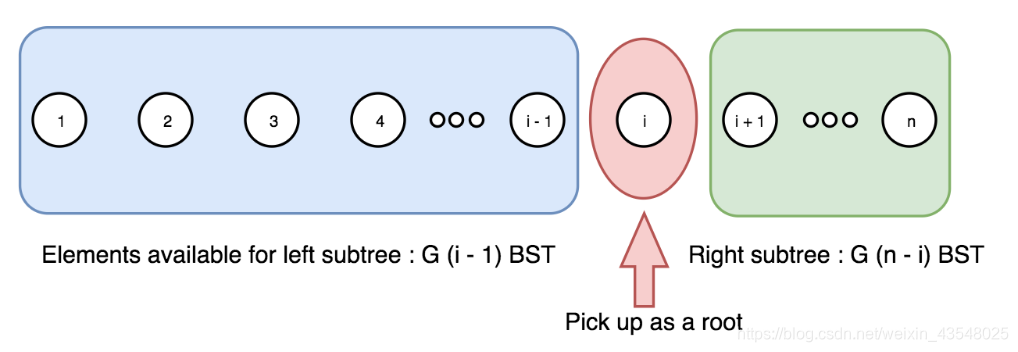
4.F(3,7)，以 3 为根的不同二叉搜索树个数。为了以 3 为根从序列 [1, 2, 3, 4, 5, 6, 7] 构建二叉搜索树，我们需要从左子序列 [1, 2] 构建左子树，从右子序列 [4, 5, 6, 7] 构建右子树，然后将它们组合(即笛卡尔积)。

我们可以将 [1,2] 构建不同左子树的数量表示为 G(2, 从 [4, 5, 6, 7]` 构建不同右子树的数量表示为 G(4)。这是由于 G(n)和序列的内容无关，只和序列的长度有关。于是，F(3,7)=G(2)⋅G(4)。 概括而言，我们可以得到以下公式：

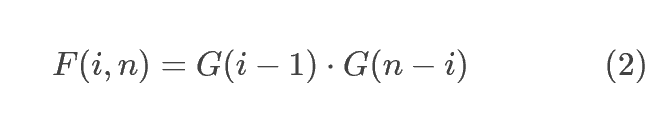
5.将公式 (1)，(2) 结合，可以得到 G(n) 的递归表达公式：

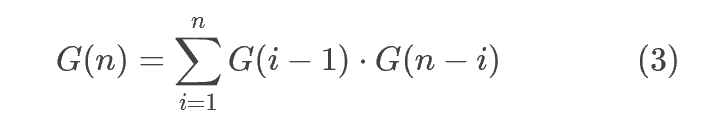
6.从小到大计算，因为 G(n) 的值依赖于 G(0)…G(n−1)。

import java.util.*;
public class Solution {
    /**
     *
     * @param n int整型
     * @return int整型
     */
    public int numTrees (int n) {
        int G[]=new int[n+1];
        //只有一个节点或者0个节点，只有一种情况
       G[0]=1;
       G[1]=1;
       //从第二个节点开始
       for(int i=2;i<=n;i++){
           for(int j=1;j<=i;j++){
               G[i]+=G[i-j]*G[j-1];
           }
       }
       return G[n];
    }
}

给定一个值n,请生成所有的存储值1...n.的二叉搜索树（BST）的结构

输入：3

输出：

[

  [1,null,3,2],

  [3,2,null,1],

  [3,1,null,null,2],

  [2,1,3],

  [1,null,2,null,3]

]

解释：

以上的输出对应以下 5 种不同结构的二叉搜索树：

 

   1         3     3      2      1

    \       /     /      / \      \

     3     2     1      1   3      2

    /     /       \                 \

   2     1         2                 3

 

二叉搜素数数量是一个 卡特兰数。

解题思路：

1.我们从序列 1 ..n 中取出数字 i，作为当前树的树根。于是，剩余 i - 1 个元素可用于左子树，n - i 个元素用于右子树。

这样会产生 G(i - 1) 种左子树 和 G(n - i) 种右子树，其中 G 是卡特兰数。

2.对序列 1 ... i - 1 重复上述过程，以构建所有的左子树；

3.对 i + 1 ... n 重复，以构建所有的右子树。

4.就有了树根 i 和可能的左子树、右子树的列表。

5.对两个列表循环，将左子树和右子树连接在根上。

import java.util.*;
/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 * }
 */
public class Solution {
    /**
     *
     * @param n int整型
     * @return TreeNode类ArrayList
     */
    public ArrayList<TreeNode> generate_tree (int start,int end){
        ArrayList<TreeNode>alltree =new ArrayList<TreeNode>();
   //如果开始大于结束，就是空
           if(start>end){
               alltree.add(null);
               return alltree;
           }
           for(int i=start;i<=end;i++){
            //递归构建左子树列表
               ArrayList <TreeNode> left_tree=generate_tree(start,i-1);
                //递归构建右子树列表
               ArrayList <TreeNode> right_tree=generate_tree(i+1,end);
          //树根 i 和可能的左子树、右子树的列表，对两个列表循环，连接在一起
               for(TreeNode l:left_tree){
                   for(TreeNode r:right_tree){
                      TreeNode node=new TreeNode(i);//定义根节点
                      node.left=l;   //左子树
                      node.right=r;  //右子树
                        alltree.add(node);
                   }
               }
           }
           return alltree;
    }
    public ArrayList<TreeNode> generateTrees (int n) {
       
         return generate_tree(1,n);
    }
}