快速幂（主矩阵，补充矩阵的基础知识和数的快速幂）另题3：s=a+a^2+……+a^k快速两求法（二分求和，矩阵分解）

最新推荐文章于 2020-10-30 17:56:30 发布

原创最新推荐文章于 2020-10-30 17:56:30 发布 · 582 阅读

1 ·

CC 4.0 BY-SA版权

杂七杂八专栏收录该内容

151 篇文章

订阅专栏

这篇博客介绍了矩阵的基本运算，包括加减和乘法，并展示了如何用C++实现。文章重点讲解了快速幂算法在数值和矩阵形式的应用，包括数的快速幂和矩阵快速幂。通过实例解析了如何解决求矩阵幂级数和斐波那契数列的末尾4位数问题，提出了二分求和与矩阵分解的高效解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

矩阵（mn）基本运算：
+/-：对应位上的数加减；
X：（nn)矩阵，c[i][j]=(c[i][j]+a[i][k]*b[k][j]);
对应代码：

for(int i=1;i<=n;i++)
 for(int j=1;j<=n;j++)
 c.m[i][j]=a.m[i][j]+(-)b.m[i][j];//+/-
 for(int i=1;i<=n;i++)
  for(int j=1;j<=n;j++)
   for(int k=1;k<=n;k++)
   c.m[i][j]=c.m[i][j]+a.m[i][k]*b.m[k][j];//*

结构体的定义：
虽可直接定义数组来使用，但为了更加简明，清楚，定义结构体
又因使用C++编译器，无需特地使用typedef struct,所以在此直接使用struct；

struct maxtrix
{
 int m[maxn][maxn]
};
int main()
{
 maxtrix c;//使用
}

单位矩阵：相当于乘法中的1

int main()
{
 maxtrix c;
 for(int i=1;i<=n;i++)
  for(int j=1;j<=n;j++)
  c.m[i][j]=(i==j);
 return 0;
}

快速幂（数）：
二进制的使用

int quickpower(int a,int k)//a^k
{
 int c=1;
 while(k)
 {
  if(k&1) c*=a;
  k>>=1;
  a*=a;
 }
 return c;
}

快速幂（矩阵）：
类似，多了一步矩阵的乘法

maxtrix mul(maxtrix a,maxtrix b)
{
  maxtrix c;
  memset(c.m,0,sizeof(c.m));
  for(int i=1;i<=n;i++)
   for(int j=1;j<=n;j++)
    for(int k=1;k<=n;k++)
    c[i][j]=(c[i][j]+a[i][k]*b[k][j])%mod;//通常数大，需取模
 return c;
}
maxtrix quickpower(maxtrix a,int k)//a^k
{
 maxtrix c;
 for(int i=1;i<=n;i++)
  for(int j=1;j<=n;j++)
  c[i][j]=(i==j);
 while(k)
 {
  if(k&1) c=mul(c,a);
  k>>=1;
  a=mul(a,a);
 }
 return c;
}

例题：
1：Tr A//熟悉基本操作
Input
数据的第一行是一个T，表示有T组数据。

每组数据的第一行有n(2 <= n <= 10)和k(2 <= k < 10^9)两个数据。接下来有n行，每行有n个数据，每个数据的范围是[0,9]，表示方阵A的内容。

    Output
    对应每组数据，输出Tr(A^k)%9973。

    Sample Input
    2
    2 2
    1 0
    0 1
    3 99999999
    1 2 3
    4 5 6
    7 8 9

    Sample Output
    2
    2686

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int mod=9973;
int n;
typedef struct
{
 int m[15][15];
}maxtrix;//比较sruct maxtrix//构建结构体
maxtrix mul(maxtrix a,maxtrix b)
{
 maxtrix c;
 memset(c.m,0,sizeof(c.m));
 for(int i=1;i<=n;i++)
  for(int j=1;j<=n;j++)
   for(int k=1;k<=n;k++)
   c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
 return c;
}//矩阵的乘法
maxtrix quickpower(maxtrix a,int k)
{
 maxtrix c;
 for(int i=1;i<=n;i++)
  for(int j=1;j<=n;j++)
  c.m[i][j]=(i==j);
 while(k)
 {
  if(k&1) 
   c=mul(c,a);
  k/=2;
  a=mul(a,a);
 }
 return c;
}//快速幂操作
int main()
{
 int t,k;
 maxtrix c;
 cin>>t;
 while(t--)
 {
  int sum=0;
  cin>>n>>k;
  for(int i=1;i<=n;i++)
   for(int j=1;j<=n;j++)
   cin>>c.m[i][j];
  c=quickpower(c,k);
  for(int i=1;i<=n;i++)
   sum=(sum+c.m[i][i])%mod;
  cout<<sum<<endl;
 }
 return 0;	
}

2：Fibonacci//基本的应用
In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …An alternative formula for the Fibonacci sequence is.
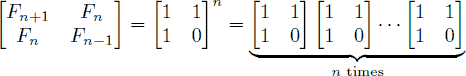
在这里插入图片描述
Given an integer n, your goal is to compute the last 4 digits of Fn.
Input

   The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.
  

    Output
    
  
   For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).
  

    Sample Input
    0
    9
    999999999
    1000000000
    -1

    Sample Output
    0
    34
    626
    6875

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2
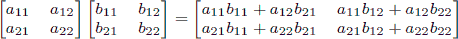
在这里插入图片描述
matrices is given by.Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:.

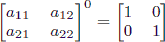
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int mod=10000;
int n;
typedef struct 
{
 int m[2][2];
}maxtrix;//构造
maxtrix mul(maxtrix a,maxtrix b)
{
 maxtrix c;
 memset(c.m,0,sizeof(c.m));
 for(int i=0;i<=1;i++)
  for(int j=0;j<=1;j++)
   for(int k=0;k<=1;k++)
   c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
 return c;
}//矩阵乘法
maxtrix quickpower(maxtrix a)
{
 maxtrix c;
 c.m[0][0]=c.m[0][1]=c.m[1][0]=1;c.m[1][1]=0;	
 while(n)
 {
 	if(n&1)
 	 c=mul(c,a);
 	n/=2;
 	a=mul(a,a);
 }
 return c;
}//快速幂
int main()
{
 while(cin>>n&&(n!=-1))
 {
  if(n==0) {cout<<0<<endl;continue;  }
  maxtrix c;	
  c.m[0][0]=c.m[0][1]=c.m[1][0]=1;c.m[1][1]=0;
  /*for(int i=0;i<=1;i++)
  {
  	for(int j=0;j<=1;j++)
	 cout<<c.m[i][j]<<" ";
	cout<<endl; 
  } */ 
  c=quickpower(c);
  /*for(int i=0;i<=1;i++)
  {
  	for(int j=0;j<=1;j++)
	 cout<<c.m[i][j]<<" ";
	cout<<endl; 
  } */ 
  cout<<c.m[1][1]%mod<<endl; 	//
 }
 return 0;	
}

3：Matrix Power Series//二分求和/矩阵分解
看了题解作者解释得很详细
Given a n × n matrix A and a positive integer k, find the sum S = A + A2 + A3 + … + Ak.
Input

   The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 109) and m (m < 104). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.
  

    Output
    
  
   Output the elements of S modulo m in the same way as A is given.
  

    Sample Input
    2 2 4
    0 1
    1 1

    Sample Output
    1 2
    2 3

主要注意点S = A + A2 + A3 + … + Ak.；
法一：二分求和

//二分求和
//当k为偶数时：
//s(k)=s(k/2)+A^(n/2) * s(k/2) 即s(k)=(E+A^(n/2))*s(n/2)  （E为单位矩阵）
//当k为奇数时：
//s(k)=s(k-1)+A^k ,  那么k-1为偶数。依照上面二分 
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,k,mod;
struct maxtrix
{
	int m[35][35];
};//构造
maxtrix add(maxtrix a,maxtrix b)
{
 for(int i=1;i<=n;i++)
  for(int j=1;j<=n;j++)
  a.m[i][j]=(a.m[i][j]+b.m[i][j])%mod;
 return a; 
}//矩阵加法
maxtrix mul(maxtrix a,maxtrix b)
{
 maxtrix c;
 memset(c.m,0,sizeof(c.m));
 for(int i=1;i<=n;i++)
  for(int j=1;j<=n;j++)
   for(int k=1;k<=n;k++)
   c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
 return c;
}//矩阵乘法
maxtrix quickpower(maxtrix a,int k1)
{
 maxtrix c;
 for(int i=1;i<=n;i++)
  for(int j=1;j<=n;j++)
  c.m[i][j]=(i==j);
 while(k1)
 {
  if(k1&1) c=mul(c,a);
  k1/=2;
  a=mul(a,a);
 }
 return c;
}//快速幂
maxtrix cal(maxtrix a,int k)
{
  if(k==1) return a;
  if(k&1)
   return add(quickpower(a,k),cal(a,k-1));
  k/=2;
  return mul(add(quickpower(a,0),quickpower(a,k)),cal(a,k)); 	
}//***二分求和，递归***
int main()
{
 cin>>n>>k>>mod;
 maxtrix c;
 for(int i=1;i<=n;i++)	
  for(int j=1;j<=n;j++)
  cin>>c.m[i][j];
 c=cal(c,k);
 for(int i=1;i<=n;i++)	
  for(int j=1;j<=n;j++)
  j==n?cout<<c.m[i][j]<<endl:cout<<c.m[i][j]<<" "; 
 return 0;
}

法二：矩阵分解

//矩阵分解
//|A  E|
//|0  E| 
//另有一种二分法， 
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int n,k,mod;
typedef struct
{
 int m[70][70];
}maxtrix;//构造
maxtrix mul(maxtrix a,maxtrix b)
{
 maxtrix c;
 memset(c.m,0,sizeof(c.m));
 for(int i=1;i<=n;i++)
  for(int j=1;j<=n;j++)
   for(int k=1;k<=n;k++)
   c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
 return c;
}//矩阵乘法
int main()
{
 cin>>n>>k>>mod;
 maxtrix c,b;
 for(int i=1;i<=n;i++)
 {
  for(int j=1;j<=n;j++)
   cin>>c.m[i][j];
  c.m[i][i+n]=c.m[i+n][i+n]=b.m[i][i]=b.m[i+n][i+n]=1; 
 } //转换新矩阵
 n*=2;k++;
 while(k)
 {
 	if(k&1) b=mul(b,c);
         /*for(int i=1;i<=n;i++)
           {
 	   for(int j=1;j<=n;j++) 
	    cout<<b.m[i][j]<<" ";
	   cout<<endl; 
           }	*/
 	k/=2;
 	c=mul(c,c);
 }
 /*for(int i=1;i<=n;i++)
    {
 	 for(int j=1;j<=n;j++) 
	  cout<<b.m[i][j]<<" ";
	 cout<<endl; 
    }	*/
 n/=2;
 for(int i=1;i<=n;i++) 
 {
  b.m[i][i+n]--;	//不要忘了减掉
  while(b.m[i][i+n]<0)//注意！！由于上一步，可能出现负数，要把mod掉的数加回来
   b.m[i][i+n]+=mod;
 }
 for(int i=1;i<=n;i++)
 {
 	for(int j=1;j<n;j++) cout<<b.m[i][n+j]<<" ";
 	cout<<b.m[i][2*n]<<endl;
 }
 return 0;
}