第一题是一个01?问题,洛谷中的采药,只有两种情况,放或者是不放,刚开始来一种二维的解法,在考虑第i种的时候 看一下背包九讲里的说法
将前i件物品放入容量为v的背包中”这个子问题,若只考虑第i件物品的策略
(放或不放),那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品,那么问题
就转化为“前i-1件物品放入容量为v的背包中”,价值为f[i-1][v];如果放第i件物品,那么问题就转
化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”,此时能获得的最大价值就是f[i-1][v-c[i]]再
加上通过放入第i件物品获得的价值w[i]
f[i][v] = Max(f[i-1][j],f[i-1][j-c[i]]+w[i]);
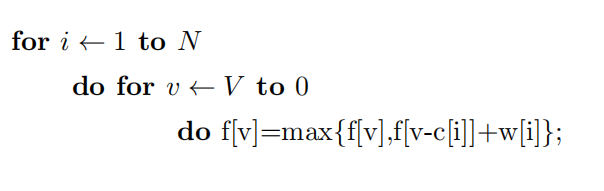
这是01背包的一维写法
贴一道洛谷上的题
P1048 采药
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入输出格式
输入格式:
第一行有22个整数T(1 \le T \le 1000)T(1≤T≤1000)和M(1 \le M \le 100)M(1≤M≤100),用一个空格隔开,TT代表总共能够用来采药的时间,MM代表山洞里的草药的数目。
接下来的MM行每行包括两个在11到100100之间(包括11和100100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式:
11个整数,表示在规定的时间内可以采到的草药的最大总价值。
输入输出样例
输入样例#1: 复制
70 3
71 100
69 1
1 2
输出样例#1: 复制
3
代码:
#include<bits/stdc++.h>
using namespace std;
int dp[101][1010];
int dp1[1010];
int times[200];
int v[200];
int main() {
int t,m;
cin>>t>>m;
for(int i=1;i<=m;i++) {
cin>>times[i]>>v[i];
}
for(int i=1;i<=m;i++)
for(int j=t;j>=0;j--) {
if(j>=times[i]) {
//dp[i][j]=max(dp[i-1][j],dp[i-1][j-times[i]]+v[i]);
dp1[j]=max(dp1[j],dp1[j-times[i]]+v[i]);
}
//else
// dp[i][j]=dp[i-1][j];
}
// cout<<dp[m][t];
// cout<<endl;
cout<<dp1[t];
}
被注释掉的地方是二维的做法,不过由于二维容易tle和mle建议不用
下面说一下优化的原理
复制的:
主循环i=1…N,每次算出来二维数组f[i][0…V]的所有值。那么,如果只用一个数组f[0…V],能不能保证第i次循环结束后f[v]中表示的就是我们定义的状态f[i][v]呢?f[i][v]是由f[i-1][v]和f[i-1][v-c[i]]两个子问题递推而来,能否保证在推f[i][v]时(也即在第i次主循环中推f[v]时)能够得到f[i-1][v]和f[i-1][v-c[i]]的值呢?事实上,这要求在每次主循环中我们以v=V…0的顺序推f[v],这样才能保证推f[v]时f[v-c[i]]保存的是状态f[i-1][v-c[i]]的值。
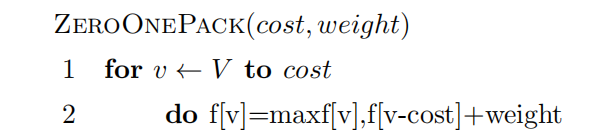
下面是完全背包 即每种物品可以放无限次

基本思路 这个问题非常类似于01背包问题,所不同的是每种物品有无限件。也就是从每种
物品的角度考虑,与它相关的策略已并非取或不取两种,而是有取0件、取1件、取2件……等很
多种。如果仍然按照解01背包时的思路,令f[i][v]表示前i种物品恰放入一个容量为v的背包的最
大权值。仍然可以按照每种物品不同的策略写出状态转移方程:
f[i][v] = max{f[i − 1][v − k × c[i]] + k × w[i]} 此处的k 0<=k*c[i]<=v
优化的话可以考虑一下性价比:
若两件物品i、j满足c[i] 6 c[j]且w[i] > w[j],则将物品j去掉,不用考虑。这个优化的正确性显然:任何情况下都可
将价值小费用高得j换成物美价廉的i,得到至少不会更差的方案。
这里又一种完全背包的解决方案:
转化为01背包问题求解 :既然01背包问题是最基本的背包问题,那么我们可以考虑把完全背
包问题转化为01背包问题来解。最简单的想法是,考虑到第i种物品最多选V/c[i]件,于是可以把
第i种物品转化为V/c[i]件费用及价值均不变的物品,然后求解这个01背包问题。这样完全没有改
进基本思路的时间复杂度,但这毕竟给了我们将完全背包问题转化为01背包问题的思路:将一
种物品拆成多件物品
for i ← 1 to N
do for v ← 0 to V
do f[v] = max{f[v], f[v − cost] + weight}
摘取一下文中所说:
你会发现,这个伪代码与P01的伪代码只有v的循环次序不同而已。为什么这样一改就可
行呢?首先想想为什么P01中要按照v=V…0的逆序来循环。这是因为要保证第i次循环中的状
态f[i][v]是由状态f[i-1][v-c[i]]递推而来。换句话说,这正是为了保证每件物品只选一次,保证在
考虑“选入第i件物品”这件策略时,依据的是一个绝无已经选入第i件物品的子结果f[i-1][v-c[i]]。
而现在完全背包的特点恰是每种物品可选无限件,所以在考虑“加选一件第i种物品”这种策略
时,却正需要一个可能已选入第i种物品的子结果f[i][v-c[i]],所以就可以并且必须采用v=0…V的顺
序循环。这就是这个简单的程序为何成立的道理。
最后得出完全背包问题的二维和一维解决模版:
f[i][v] = Max(f[i − 1][v],f[i][j-c[i]]+w[i]
将这个方程用一维数组实现,便得到了上面的伪代码。
最后抽象出处理一件完全背包类物品的过程伪代码:
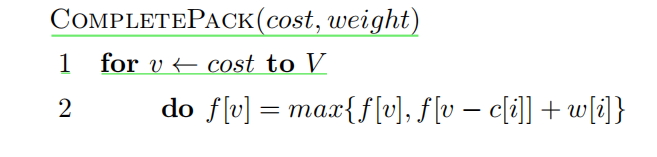
最后贴一道题: 也是洛谷的 上面那道题的改编版
P1616 疯狂的采药
题目描述
LiYuxiang是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同种类的草药,采每一种都需要一些时间,每一种也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是LiYuxiang,你能完成这个任务吗?
此题和原题的不同点:
1.每种草药可以无限制地疯狂采摘。
2.药的种类眼花缭乱,采药时间好长好长啊!师傅等得菊花都谢了!
输入输出格式
输入格式:
输入第一行有两个整数T(1 <= T <= 100000)和M(1 <= M <= 10000),用一个空格隔开,T代表总共能够用来采药的时间,M代表山洞里的草药的数目。接下来的M行每行包括两个在1到10000之间(包括1和10000)的整数,分别表示采摘某种草药的时间和这种草药的价值。
输出格式:
输出一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
输入输出样例
输入样例#1: 复制
70 3
71 100
69 1
1 2
输出样例#1: 复制
140
说明
对于30%的数据,M <= 1000;
对于全部的数据,M <= 10000,且M*T<10000000(别数了,7个0)。
代码:包括二维和一维的
#include<bits/stdc++.h>
using namespace std;
int dp[100010];
int dp2[1010][10010];
int w[100010];
int v[100010];
int main() {
int t,m;
cin>>t>>m;
for(int i=0;i<m;i++)
cin>>w[i]>>v[i];
for(int i=0;i<m;i++)
for(int j=w[i];j<=t;j++)
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
cout<<dp[t];
cin>>t>>m;
memset(w,0,sizeof(w));
memset(v,0,sizeof(v));
for(int i=0;i<m;i++)
cin>>w[i]>>v[i];
int maxn=-10000;
for(int i=0;i<m;i++) {
for(int j=w[i];j<=t;j++) {
dp2[i][j]=max(dp2[i-1][j],dp2[i][j-w[i]]+v[i]);
maxn=max(maxn,dp2[i][j]);
}
}
cout<<maxn;
}








 本文深入探讨了背包问题的两种主要类型——01背包和完全背包,提供了详细的算法解释和代码示例,包括一维和二维的解决方案,以及如何优化计算过程。
本文深入探讨了背包问题的两种主要类型——01背包和完全背包,提供了详细的算法解释和代码示例,包括一维和二维的解决方案,以及如何优化计算过程。
















 1097
1097

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








