数据结构：图

什么是“图”（Graph）

含义

• 表示“多对多”的关系

• 包含

  • 一组顶点：通常用 V (Vertex) 表示顶点集合

  • 一组边：通常用 E (Edge) 表示边的集合

  • 边是顶点对：(v, w)属于E ，其中 v, w属于 V 

  • 有向边 < v, w> 表示从v指向w的边（单行线）

  • 不考虑重边和自回路

常见术语

• 无向图：边有方向

• 有向图：边无方向

• 网络：边有权重

表示方法

邻接矩阵G[N][N]——N个顶点从0到N-1编号

• G[i][j] =1 若<vi,vj>是G中的边

• G[i][j] =0 否则

邻接矩阵的优化

• 用一个长度为N(N+1)/2的1维数组A存储

• G（ij）在A中对应的下标是： ( i(i+1)/2 + j )

• 对于网络，只要把G[i][j]的值定义为边 <vi,vj>的权重即可。

邻接表

• G[N]为指针数组，对应矩阵每行一个链表，只存非0元素;

• 把与自己相连的点，串成表

• 对于网络，结构中要增加权重的域。

• 对于有向表，结构中要增加方向的域。

图的遍历

深度优先搜索

按线搜索，适合方向已知

​

广度优先搜索

按层搜索，适合距离已知

​

图不连通怎么办？

概念

• 连通图：图中任意两顶点均连通

• 简单路径：如果V到W之间的所有顶点都不同

• 连通分量：无向图的极大连通子图（）

• 强连通：有向图中顶点V和W之间存在双向路径，则称V和W是强连通的

• 强连通图：有向图中任意两顶点均强连通

• 强连通分量：有向图的极大强连通子图

解决方案

​

最短路径问题

• 无权图的单源最短路算法

  递增（非递减）的顺序找出到各个顶点的最短路（BFS）

• 有权图的单源最短路算法

  • Dijkstra算法

    一个点一个点的扫（从距离最小者开始），不断更新被扫点的相邻点的最小距离（当被扫点的到源点的距离+相邻点到被扫地的距离 < 相邻点到源点的距离）

  • 实现

    • 方法1：直接扫描所有未收录顶点（稠密图效果好） O( |V|^2 + |E| )

    • 方法2：将dist存在最小堆中（稀疏图效果好） O( |E| log|V| )

• 多源最短路算法

  • 方法1：直接将单源最短路算法调用|V|遍（稀疏图效果好）T = O( |V|3 + |E| |V|)

  • 方法2：Floyd算法

最小生成树（边的权重和最小）

• 贪心算法

  • 贪：每一步都要最好的

  • 好：权重最小的边

• 约束：|V|-1条边；不能有回路

• Prim算法（让一棵小树长大）

  • 与树相邻的点中选择相邻边权重最小的加入树，从而使树不断生长，直至囊括所有节点（加入了V-1次）

  • T = O( |V|^2 ); 稠密图合算

• Kruskal算法（将森林合并成树）

  • 在未连接点选择中权重最小的边，连接，但不能与已连接的边构成回路，直至有（v-1条边）

  • T = O( |E| log |E| );稀疏图合算

拓扑排序

• AOV网络

  

• 拓扑排序：根据Aov网络进行排序，必须满足前提条件在前

• 先去入度为零的顶点，每一个邻接点的入度-1，若领接点的入度为0，则存入队列，删除数不等于顶点个数则存在回路。

• AOE网络

  

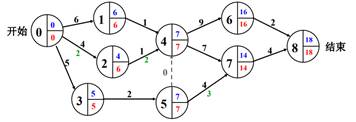
• AOE中，边为项目，顶点为时间节点，顶点由编号（黑）、最早完成时间（蓝）、最晚完成时间（红）组成。