SVM4—核方法

核方法

$\bullet$ 前面我们用超平面（线性模型）来分开不同类型的训练箱体
$\bullet$ 但在实际任务中，原始样本空间也许不存在一个超平面能将训练样本分开，例如：
$\bullet$ 对这类问题，我们可以将原始空间映射到一个更高维的空间，使得在这个特征空间数据线性可分
$\bullet$ 令$\varphi (\mathbf{x})$表示将$\mathbf{x}$映射后的特征向量，则在特征空间划分超平面对应的模型可表示为：$$f(\mathbf{x})={\mathbf{w}}^T\varphi (\mathbf{x})+b$$
$\bullet$ 根据之前SVM的推导，得到特征映射后的SVM目标函数为：$$mi{n}_{w,b}=\frac{1}{2}||\mathbf{w}|{|}_2^2+C\sum _{i=1}^N{\xi }_i$$$$s.t.y_i({\mathbf{w}}^T\varphi (\mathbf{x})+b)>=1-{\xi }_i，i=1,...,N$$$${\xi }_i>0,i=1,...,N$$

核方法—对偶

$\bullet$ 相应的对偶问题为：
$$ma{x}_{\alpha }\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j<\varphi ({\mathbf{x}}_i),\varphi ({\mathbf{x}}_i)>$$$$s.t.0<={\alpha }_i<=C,i=1,...,N$$$$\sum _{i=1}^N{\alpha }_i{y}_i=0$$
$\bullet$ 求得对偶问题的解$\alpha$后，可计算$\mathbf{w}，b$，从而得到分类判别函数：$$f(\mathbf{x})={\mathbf{W}}^T\varphi (\mathbf{x})+b$$$$=\sum _{i=1}^N{\alpha }_i{y}_i<\varphi ({\mathbf{x}}_i),\varphi (\mathbf{x})>+b$$

核技巧

$\bullet$ 将问题变为对偶问题：只需计算点积
　　１)在SVM中，最大化下列目标函数

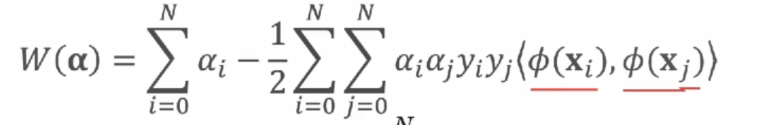
　　2）判别函数为：
$\bullet$ 由于特征空间维数可能很高（甚至无穷维），直接计算特征空间的点积通常是困难的
$\bullet$ 核函数：高维空间中的点积可写成核(kernel)的形式$$K({\mathbf{x}}_i,{\mathbf{x}}_j)=<\varphi ({\mathbf{x}}_i),\varphi ({\mathbf{x}}_j)>$$老师说到点积的时候，说也就是相似度，那么应如何理解呢？
$\bullet$ 选定核函数，无需计算映射$\varphi (\mathbf{x})$就可以计算点积
　　１）SVM核化目标函数为　　2）预测模型为没有+b这一项吗

构造核函数

$\bullet$ 一种核函数的构造方式是显示地定义一个特征映射$\varphi (.)$，将每个输入x映射到$\varphi (\mathbf{x})$，从而得到核函数的间接定义$$k(\mathbf{x},{\mathbf{x}}^{\prime })=\varphi (\mathbf{x}{)}^T\varphi ({\mathbf{x}}^{\prime })$$其中的$\varphi (\mathbf{x})$称为基函数。相对于直接求点积，这种方式好像也不能节省开销吧，因为最终还是要求点积。
$\bullet$ 显示定义特征映射的情况下，核函数为特征空间（可能为无限维）中的内积。
$\bullet$ 另一种可选方式是直接定义核函数，此时需保证核函数是有效核。令x为输入空间，k(.,.)是定义在x*x上的对称函数，则k是核函数的充要条件是对已任意数据 D = { x 1 , . . . , x N } D = \{x_{1},...,x_{N}\} D={x1​,...,xN​}，则核矩阵K总是半正定的。正定、半正定的准确定义？对于一个半正定核矩阵，总是能找到一个与之对应的$\varphi$。任何一个核函数都隐式定义了一个再生Hibert空间。
可以通过找到$\varphi$ ，找到K，也可以直接找到K，这样必然会有一个$\varphi$存在，但再回去找已经没意义了，因为最终需要的就是K。

多项式核

X和X’是原始空间的特征，粗略一看，还是要求点击啊，不是说求点击开销很大吗，最后不还是要求吗？多项式阶数越高，模型越复杂。

RBF核

这里的$\sigma$跟高斯分布就是有一定的关系。RBF核最常用，只能应用于数字，通过带宽可以变成任意一个复杂的函数（这句话不好理解啊），除此，还存在其他类型的核，比如sigmoid核、tanjian核等。$\sigma$越大，模型越简单。

更多核函数

此处闭包的解释，进行上边那些运算后，得到的依然是核函数。

小结

$\sigma$越大，模型越简单，多项式阶数越高，模型越复杂。他们会严重影响到模型的性能。Logistic回归和线性回归，也可以通过核函数，得到非线性的模型。