Logistic回归7—类别样本不均衡

不平衡数据出现的场景

$\bullet$ 搜索引擎的点击预测：点击的网页往往占据很小的比例。
$\bullet$ 电子商务领域的商品推荐：推荐商品被购买的比例很低
$\bullet$ 信用卡欺诈检测。明显不存在欺诈风险的样本更多，若来一个新样本，什么都不做，直接判断不存在欺诈风险，其正确率也会很高，但着是没意义的，因为我们关注的是存在欺诈风险的异常事件。
$\bullet$ 网络攻击识别

解决方案

$\bullet$ 从数据的角度：抽样，从而使得不同类别的数据相对均衡。
$\bullet$ 从算法的角度：考虑不同误分类情况代价的差异性对算法进行优化。

抽样

$\bullet$ 随机欠抽样：从多数类中随机选择少量样本再合并原有少数样本作为新的训练数据集。会造成一些损失，选取的样本可能有偏差。数据会变小，机器处理起来压力会小一些。包括：
　　a) 有放回抽样。
　　 b)无放回抽样。
$\bullet$ 随机过抽样：随机复制少数类样本。扩大了数据集，造成模型训练复杂度加大，另一方面也造成模型的过拟合。少数类样本增多，会使得学习器特别关注这些样本，会对这部分数据造成过拟合。（过拟合好像不太好理解，是不是可以从权重的角度来理解呢？难道过抽样就没有有放回和无放回的区别吗？）

集成学习

$\bullet$ EasyEnsemble算法
　　a）对于多数类样本，通过n次有放回抽样生成n份子集；n份子集，应该是每个包括很多样本那样的n份子集。
　　b）少数样本分别和这n份样本合并训练一个模型：n个模型
　　c）最终模型：n个模型预测结果的平均值
$\bullet$ BalanceCascade（级联）算法
　　a）从多数类中有效选择一些样本与少数类样本合并为新的数据集进行训练
　　b）训练好的模型对每个多数类样本进行预测。若预测正确，则不考虑将其作为下一轮的训练样本。
　　c）依次迭代直到满足某一条件停止，最终的模型是多次迭代模型的组合。
　　老师说到预测错误的少数类样本也会成为下一轮训练的样本，跟PPT上有出入啊，当然多数类样本也说道了。多次迭代模型的组合，应该指的不是只使用最后一个吧？

SMOT: Synthetic Minority Over-sampling Technique

$\bullet$ 基本思想：基于插值为少数类合成新的样本
$\bullet$ 对少数类的一个样本i，其特征向量为${\mathbf{x}}_i$：
　　1）从少数类的全部N个样本中找到样本${\mathbf{x}}_i$的K个近邻（如欧式距离），记为${\mathbf{x}}_{i(near)}$， n e a r ∈ { i , . . . , K } near \in \{i,...,K\} near∈{i,...,K}；
　　2）从这$K$个近邻中随机选择一个样本$x_{i(nn)}$，再生成一个0到1之间的随机数$\zeta$，从而合成一个新的样本：${\mathbf{x}}_{i1}=(1-\zeta ){\mathbf{x}}_i+\zeta x_{i(near)}$
　　3）新样本：样本$x_i$和表示样本${\mathbf{x}}_{i(nn)}$的点之间所连线段上的一个点：插值。
　　
$\bullet$ SMOTE算法摈弃了随机过采样复制样本的做法，可以防止随机过采用过拟合的问题。实践证明此方法可以提高分类器的性能。
$\bullet$ SMOTE对高维数据不是很有效。高维数据一般都比较稀疏，即使是找到最近的邻居，可能也比较远，这样合成的新样本也不是很有意义。
$\bullet$ 当生成合成性实例时，SMOTE并不会把其他类的相邻实例考虑进来，这导致了类重叠的增加（下图红线上的点就是重叠的效果），并引入额外噪音。为了解决这一缺点，人们提出了一些改进算法，Borderline—SMOTE就是一种改进算法。

以上所讲处理类别不均衡技术的工具包

https://github.com/scikit-learn-contrib/imbalanced-learn

代价敏感学习（属于算法层面的方法）

$\bullet$ 在算法层面上解决不平稳数据的方法主要是基于代价敏感学习算法(Cost-Sensitive Learning)
$\bullet$ 代价敏感学习方法的核心要素是核心矩阵：不同类型的误分类情况导致的代价不一样

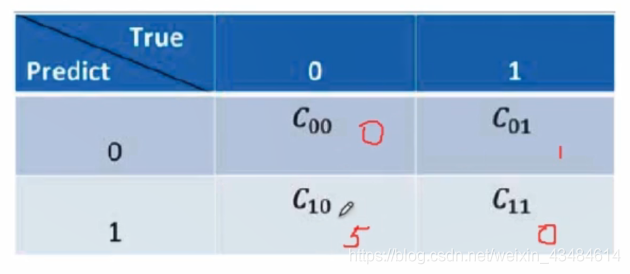
$\bullet$ 基于代价矩阵分析，代价敏感学习方法主要有以下三种实现方式(看起来好像不是三种，具体的算法也不太明白)：

Scikit-Learn中的不均衡样本分类处理

$\bullet$ 类别权重class_weight
$\bullet$ 样本权重sample_weight
　　类别不均衡问题一般用类别权重就很合适。样本权重适用于不同设备采集数据精度存在差异的情况，精度高的可以权重高一些。如果两个权重都设置，最终是乘积的关系，但好像不是简单的乘积，因为两个0.6乘积之后，就更小了，但后面的PPT就是这样简单的乘积的，应再仔细思考。

类别权重class_weight

$\bullet$ class_weight参数用于标示分类模型中各类别样本的权重
　　1）若不考虑权重，则所有类别权重相同
　　2）balanced：自动计算类别权重。某类的样本量越多，其权重越低；样本量越少，权重越高。计算方法为：$$n\_samples/(n\_classes\ast np.bincount(y))$$　　其中n_sample为样本数，n_classes为类别数，np.bincount(y)输出每个类的样本数（应该是输出对应类的样本数吧？）。
　　3）手动指定各个类别的权重。如对于0，1二类分类问题，可以定义class_weight={0:0.9, 1:0.1}，即类别0的权重为90%，而类别1的权重为10%。

样本权重class_weight

权重是放在损失函数之前，与损失函数相乘的。