【机器学习算法】【二】线性回归 逻辑回归(logistic) 非线性假设 softmax

Logistic Regression 和 Linear Regression：

• Linear Regression： 输出一个标量 wx+b，这个值是连续值，所以可以用来处理回归问题。
• Logistic Regression：把上面的 wx+b 通过 sigmoid函数映射到(0,1)上，并划分一个阈值，大于阈值的分为一类，小于等于分为另一类，可以用来处理二分类问题。
  更进一步：对于N分类问题，则是先得到N组w值不同的 wx+b，然后归一化，比如用 softmax函数，最后变成N个类上的概率，可以处理多分类问题。

神经网络用于 分类 和 回归:

• 用于回归：最后一层有m个神经元，每个神经元输出一个标量，m个神经元的输出可以看做向量 v，现全部连到一个神经元上，则这个神经元输出wv+b，是一个连续值，可以处理回归问题，跟上面 Linear Regression 思想一样。
• 用于N分类：现在这m个神经元最后连接到 N 个神经元，就有 N 组w值不同的 wv+b，同理可以归一化（比如用 softmax ）变成 N个类上的概率。

一、线性回归

利用大量的样本$D={(x_i,y_i)}_{i=1}^N$通过有监督的学习，学习到由x到y的映射f ，利用该映射关系对未知的数据进行预估，因为y为连续值，所以是回归问题。

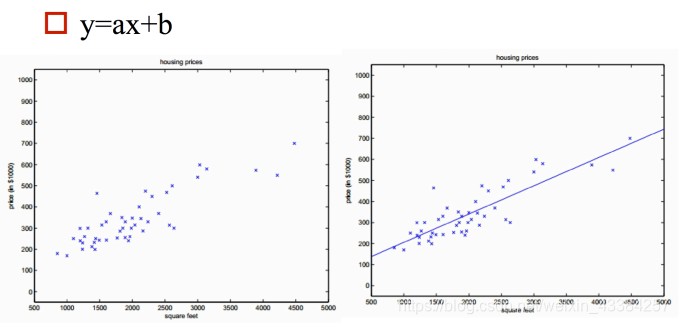
• 单特征
  结果只由一个特征决定。$h_{\theta }={\theta }_0+{\theta }_{1}x$
  
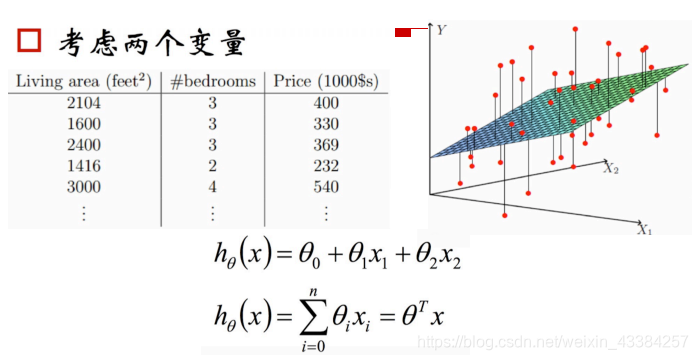
• 多特征
  结果由多个特征共同决定。$h_{\theta }={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+......++{\theta }_n{x}_n$
  

1.1 线性回归的表达式

1. 假设函数

• 线性回归的假设函数：$h_{\theta }={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+......++{\theta }_n{x}_n$
• 向量形式($\theta$和$x$都是向量)：$h_{\theta }={\theta }^{T}x$

2. 损失函数
   如何衡量已有的参数$\theta$的好坏？
   利用损失函数来衡量，损失函数度量预测值和标准答案的偏差，不同的参数有不同的偏差，所以要通过最小化损失函数，也就是最小化偏差来得到最好的参数。
   损失函数的表达式：
   $$J({\theta }_0,{\theta }_1,......,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)}-y(i)){)}^2$$
   解释：因为有m个样本，所以要平均，分母的2是为了求导方便
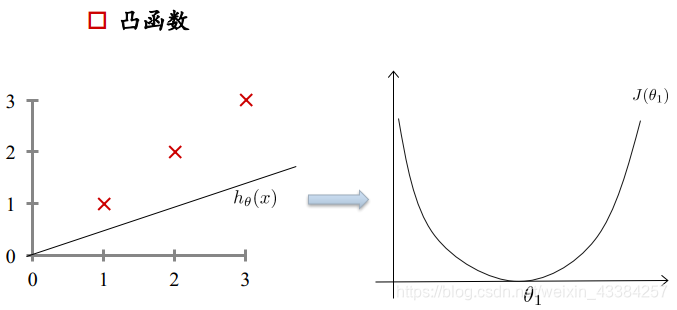
   损失函数：凸函数
3. 过拟合和欠拟合
   https://blog.youkuaiyun.com/weixin_43384257/article/details/96719641
4. 正则化解决过拟合

正则化的作用：
① 控制参数变化幅度，对变化大的参数惩罚
② 限制参数搜索空间

正则化通俗理解一下：
just right：${\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$
overfit(过拟合)：${\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3+{\theta }_4{x}^4$
$min\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+1000{\theta }_3^2+1000{\theta }_4^2$
为了使损失函数小，会导致${\theta }_3=0,{\theta }_4=0$
最终变为了：${\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$解决了过拟合

添加正则化的损失函数：$$J({\theta }_0,{\theta }_1,......,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\frac{1}{2m}\sum _{j=1}^n{\theta }_j^2$$

m：样本有m个
n：n个参数，对n个参数进行惩罚

过拟合可以简单的描述为参数过多（或者说特征太多，或者训练样本相对不足），如果λ过大，那么要想使整体的Loss下降，参数θ必然会很小，我们假设λ非常大，那么就会有很多的θ接近数值0，得到的很多接近0的数和特征相乘，就是说忽略了很多（可能导致过拟合）特征。 所以说，λ大θ小，是通过减小特征的数目（参数数目）来缓解过拟合。
eg：λ过大$⟶$${\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4$惩罚太大$⟶$可能导致${\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4$都为0$⟶$那么$h_{\theta }(x)={\theta }_0$$⟶$欠拟合了

二、逻辑回归

• 分类的本质：在空间中找到一个决策边界来完成分类的决策
• 逻辑回归：线性回归可以预测连续值，但是不能解决分类问题，我们需要根据预测的结果判定其属于正类还是负类。所以逻辑回归就是将线性回归的$(-\infty ,+\infty )$结果，通过sigmoid函数映射到(0,1) 之间。
  sigmoid：
  

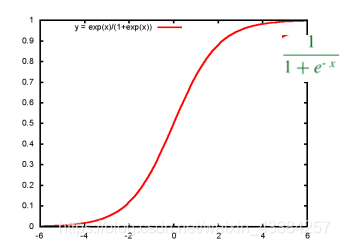
线性回归决策函数：$h_{\theta }(x)={\theta }^{T}x$
将其通过sigmoid函数，获得逻辑回归的决策函数：$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$

2.1 逻辑回归的表达式

1. 损失函数
   线性回归的损失函数为平方损失函数，如果将其用于逻辑回归的损失函数，则其数学特性不好，有很多局部极小值，难以用梯度下降法求最优。
   

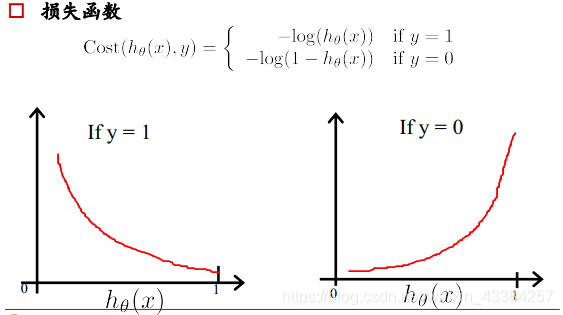
如果一个样本为正样本，那么我们希望将其预测为正样本的概率p越大越好，也就是决策函数的值越大越好，则logp越大越好，逻辑回归的决策函数值就是样本为正的概率；
如果一个样本为负样本，那么我们希望将其预测为负样本的概率越大越好，也就是(1-p)越大越好，即log(1-p)越大越好。

把上面y=1和y=0的损失函数拟合到一起：
$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}\log (h_{\theta }(x^i)+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]$$
2. 正则化解决过拟合：
$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}\log (h_{\theta }(x^i)+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$

三、梯度下降法

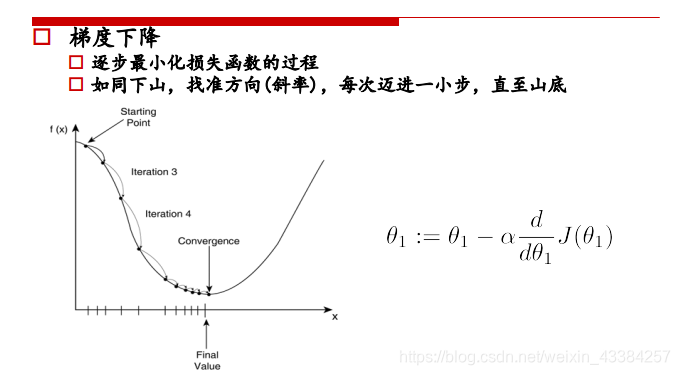
普通梯度下降法：

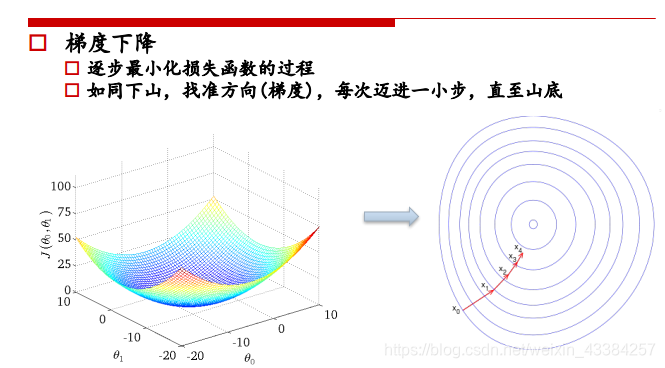
一种可以自动使J最小的${\theta }_0{\theta }_1$的算法，初始化一个$({\theta }_0,{\theta }_1)$从某个表面开始下降，初始点不同可能落在不同的局部最小值点。

• 单特征
  
  

• 多特征
  
  

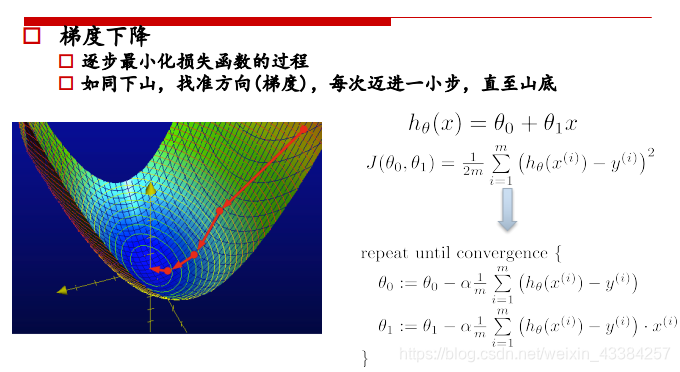
带正则化的梯度下降法：

加入正则化后更新${\theta }_j$：
$${\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$$
$${\theta }_j:={\theta }_j-\alpha (\frac{1}{m}\sum _{i=1}^m{h}_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_j)$$
$$:={\theta }_j(1-\alpha \frac{\lambda }{m})-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$
$(1-\alpha \frac{\lambda }{m})$略小于1，所以${\theta }_j(1-\alpha \frac{\lambda }{m})={\theta }_j$那么，加入正则项和不加正则项，在进行更新$\theta$时都差不多结果。

非线性假设

即使我们只考虑50x50象素的小图片，我们要分析的特征x也有2500个，如果是彩色图片将会是7500个，就算只考虑二次项，也会有3million项的特征组合，这个结果对我们之前所使用的logistic回归算法来说过于复杂。所以这种复杂的问题（特征过多），我们要使用神经网络算法。

softmax

既然logistic回归已经可以解决分类问题了，那为什么还要softmax呢？这只是忽然想到的一个问题，所以搜了一下，简单理解了一下~
下面只是简单的理解一下softmax的意义，至于具体的另外再写一篇博客把

Logistic 回归与 Softmax 回归是两个基础的分类模型，虽然听名字像是回归模型，实际上并非如此。Logistic 回归，Softmax 回归以及线性回归都是基于线性模型。其实 Softmax 就是 Logistic 的推广，Logistic 一般用于二分类，而softmax 是多分类。

Logistic 回归可以通过推广到 SoftMax 回归来解决多分类问题。下面通过实例介绍 SoftMax 回归与多个 Logistic 回归二分类的区别。

使用 SoftMax 回归或者是多个 Logistic 回归二分类解决多分类问题，取决于类别之间是否互斥，例如，如果有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的 SoftMax 回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为5）。

如果四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用 4 个二分类的 Logistic 回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。

参考：

https://blog.youkuaiyun.com/jiaoyangwm/article/details/81139362#commentBox
https://blog.youkuaiyun.com/up_XCY/article/details/88941068
https://www.cnblogs.com/zongfa/p/8971213.html
https://blog.youkuaiyun.com/huangfei711/article/details/79801968
https://blog.youkuaiyun.com/chnguoshiwushuang/article/details/80514626
https://blog.youkuaiyun.com/laobai1015/article/details/83059178