算法导论学习笔记15_最小生成树

---

1. 最小生成树（MST）

定义：图$G=(E,V)$的生成树是包含其所有结点的无环连通子图，有权图的最小生成树是其权值之和最小生成树。

下图展示了有权图的最小生成树：

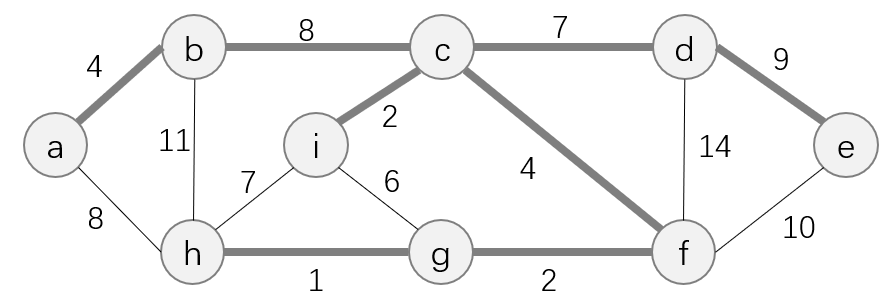
其中，加粗的边和所有的结点构成了图$G$的最小生成树。由于最小生成树中肯定不含回路，因此最小生成树中共包含图$G$中的$|V|-1$条边。

此图中，最小生成树$T$中边的权值之和为$\omega (T)=\sum _{(u,v)\in T}\omega (u,v)=4+8+7+9+2+4+1+2=37$。

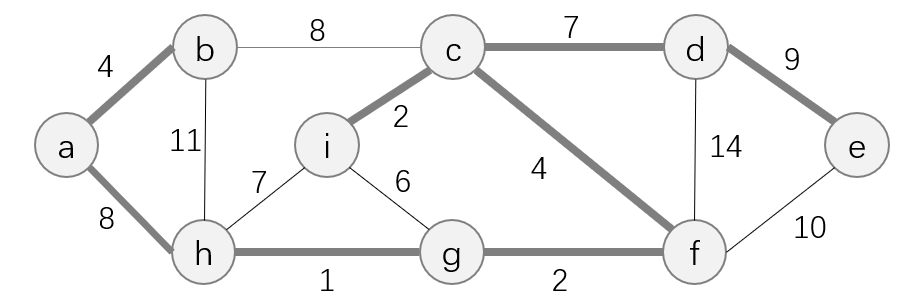
此外，有权图的最小生成树不唯一。下图所示生成树也是图$G$的最小生成树，其权值之和也为37。

2. 贪心选择性质

在利用贪心策略形成最小生成树之前，先讨论如何进行贪心选择边来形成最小生成树。

假设$T$是某棵最小生成树，$A$是最小生成树$T$的一个子集，即$A\subseteq T$，如下图蓝色加粗部分为灰色加粗部分的一个子集。

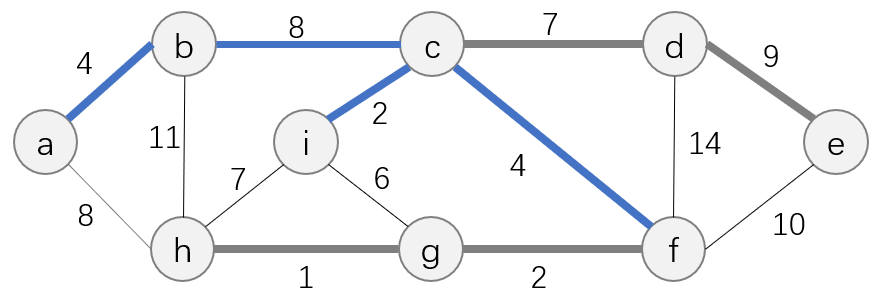
进一步是寻找一条边$(u,v)$，使得$A\cup (u,v)$仍然是某一棵最小生成树$T$的子集，称这样的边为安全边。

因此，贪心选择就是找到这样一条安全边，然后让其加入集合$A$。

下面将介绍辨认安全边的规则：

首先给出四个定义：

切割：无向图$G=(V,E)$的一个切割$(S,V-S)$是集合$V$的一个划分。例如下图中，将所有结点划分为 { a , b , d , e } \{a, b, d, e\} {a,b,d,e}和 { c , f , g , h , i } \{c, f, g, h, i\} {c,f,g,h,i}两个部分。

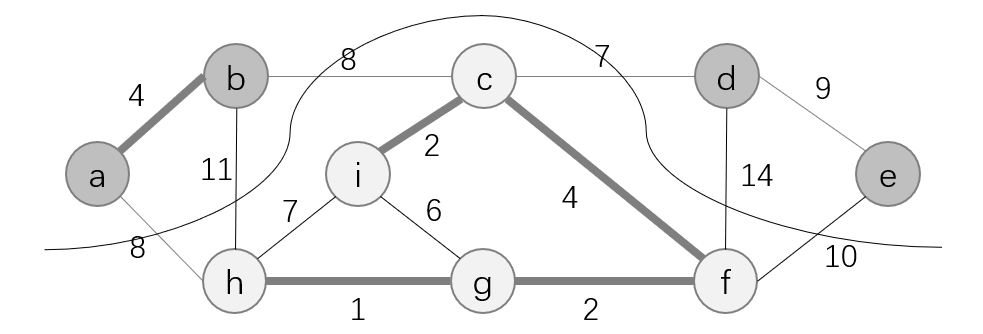
横跨：如果一条边$(u,v)\in E$的一个端点位于集合$S$， 另一个端点位于集合$V-S$， 则称该条边横跨切割$(S,V-S)$。例如上图中的$(a,h)、(b,h)、(b,c)、(c,d)、(d,f)、(f,e)$五条边就横跨切割$(S,V-S)$。

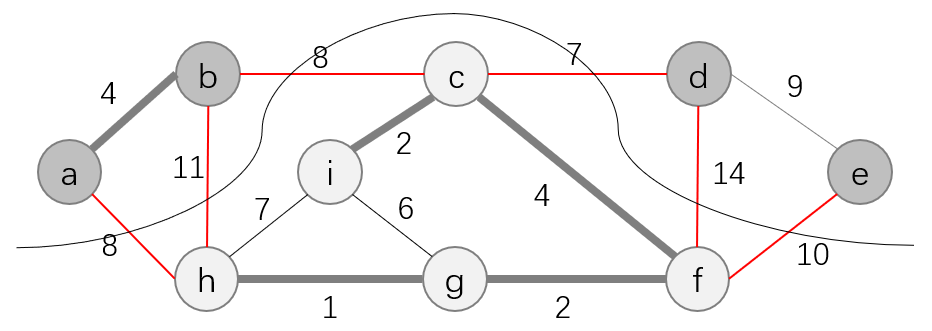
尊重：如果集合$A$中不存在横跨该切割的边，则称该切割尊重集合$A$。

轻量级边：在横跨一个切割的所有边中，权重最小的边称为轻量级边。如下图中的边$(c,d)$。

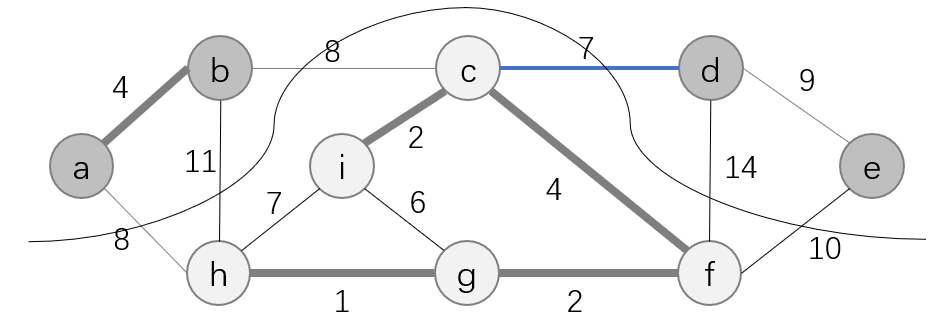
然后给出辨认安全边的规则：

定理：设$G=(V,E)$是一个在边$E$上定义了实数值权重函数$\omega$的连通无向图。设集合$A$为$E$的一个子集，且$A$包括在图$G$的某棵最小生成树中，设$(S,V-S)$是图$G$中尊重集合$A$的任意一个分割 ，又设$(u,v)$是横跨切割$(S,V-S)$的一条轻量级边。那么边$(u,v)$对于集合$A$是安全的。

根据定理的描述可知，上图中的边$(c,d)$对于集合 A = { ( a , b ) ， ( i , c ) ， ( c , f ) ， ( f , g ) ， ( g , h ) } A=\{(a, b)，(i, c)，(c, f)，(f, g)，(g, h)\} A={(a,b)，(i,c)，(c,f)，(f,g)，(g,h)}是安全边。

根据上述定理可得到推论如下：
推论：设$G=(V,E)$是一个在边$E$上定义了实数值权重函数$\omega$的连通无向图。设集合$A$为$E$的一个子集，且$A$包括在图$G$的某棵最小生成树中，并设$C=(V_c,E_c)$为森林$G_A=(V,A)$中的一个连通分量(树)。如果边$(u,v)$是连接$C$和$G_A$中某个其他连通分量的一条轻量级边，则边$(u,v)$对于集合$A$是安全的。

3. Kruskal算法

Kruskal算法找到安全边的方法是，在所有连接森林中两棵不同树的边里面，找到权值最小的边$(u,v)$。根据前面的推论可知，该权值最小的边$(u,v)$就是一条轻量级边。

Kruskal算法的流程为：首先将图$G=(V,E)$中的$|V|$个结点创建$|V|$棵树，并且将所有的边按照权重由小到大进行排序，然后按照顺序对每条边$(u,v)$进行判断，如果结点$u$和结点$v$属于两棵不同的树，则将边$(u,v)$加入最小生成树子集$A$中，并将它们各属的两棵树进行合并。通过对所有的边进行判断之后就可以得到最小生成树$T$。

Kruskal算法的伪代码如下：

MSKE_KRUSKAL(G， w)
	A = φ
	for each vertex v ∈ G.V
		MAKE_SET(v)
	sor the edges of G.E into nondecreasing order by weight w
	for each edge(u, v) ∈ G.E, taken in nondecreasing order by weight
		if FIND_SET(v) ≠ FIND_SET(v)
			A = A ∪ {(u, v)}
			UNION(u, v)
	return A

Kruskal算法的过程如下：



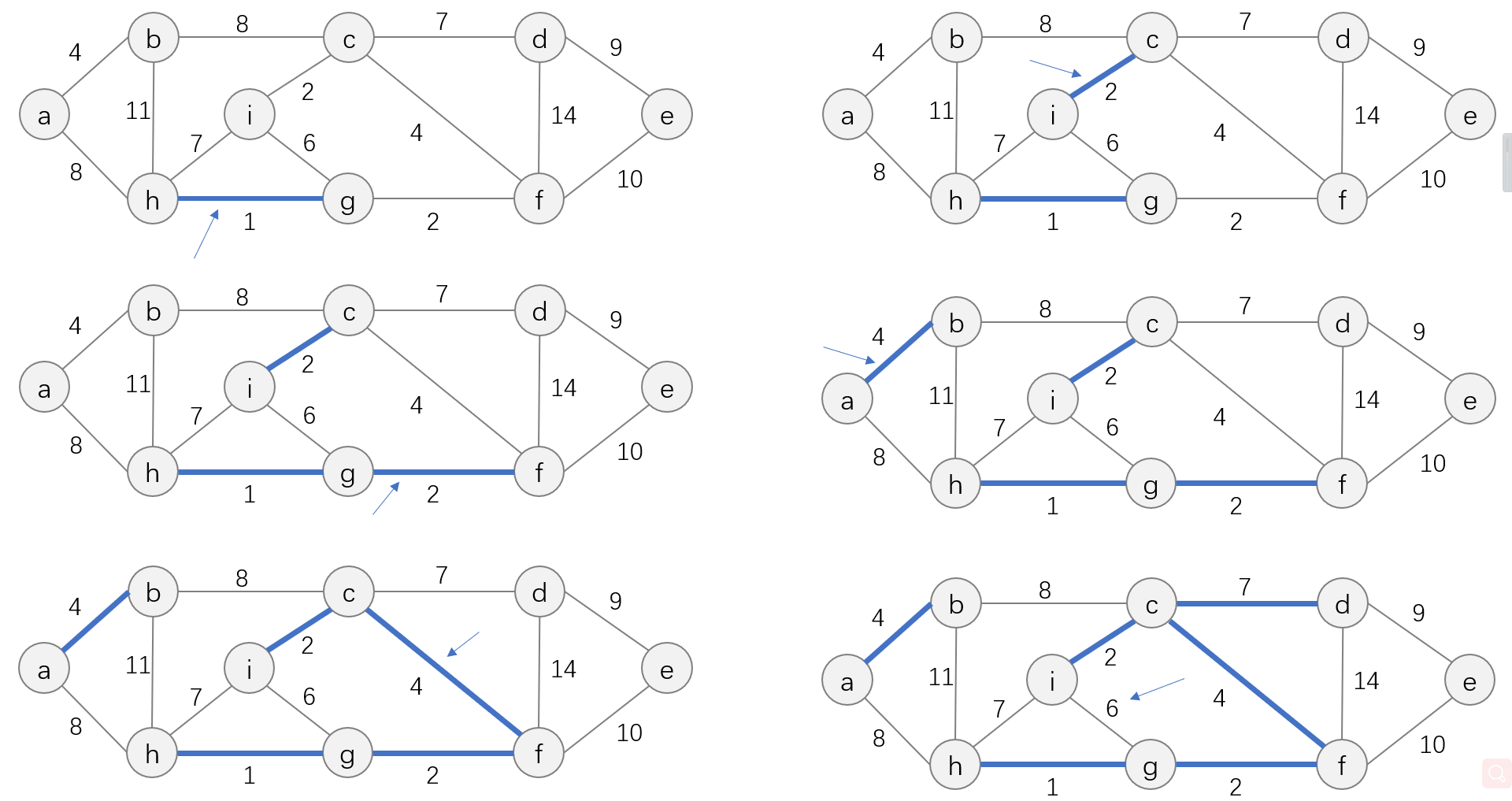
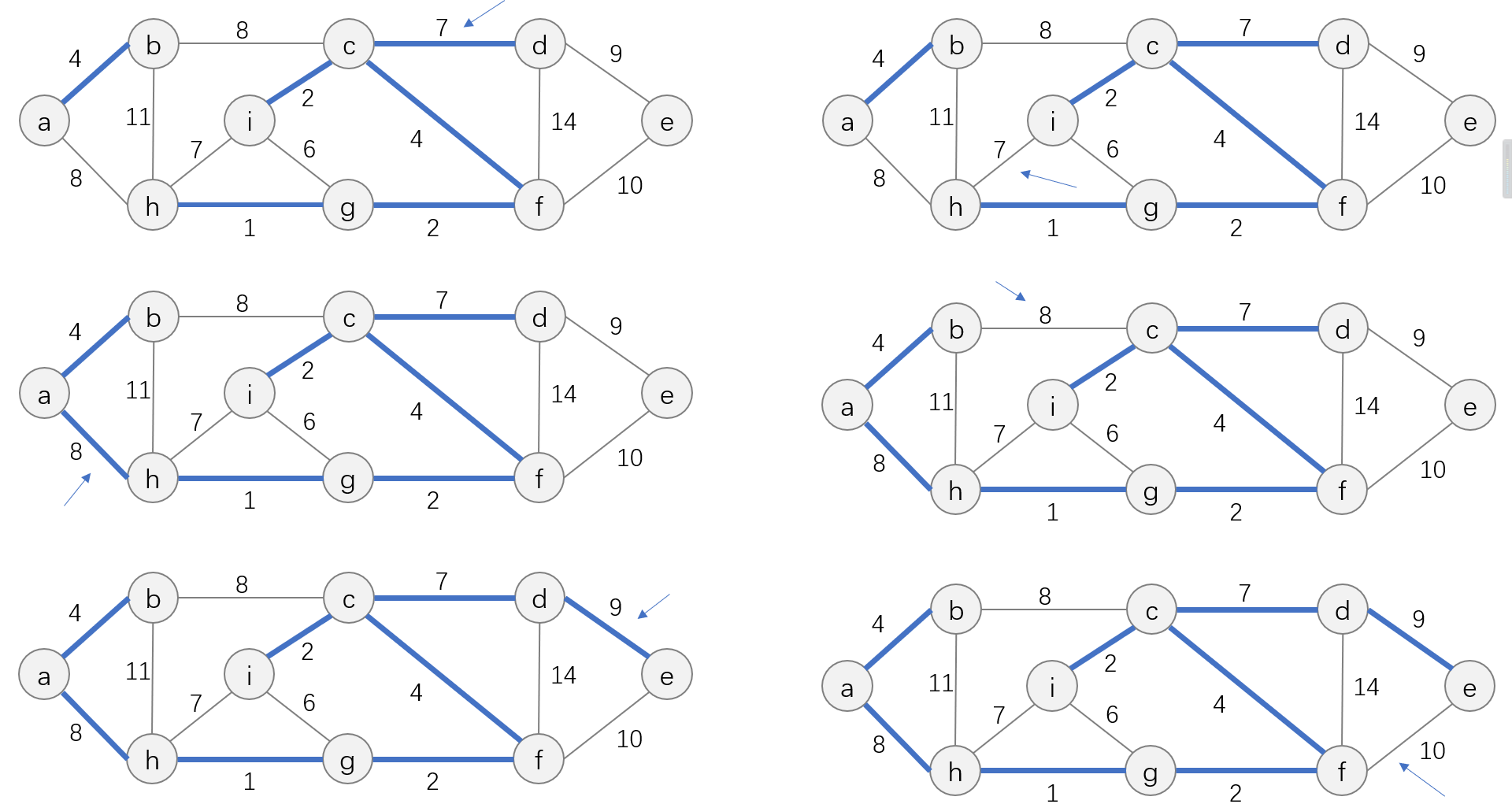
当算法初始的时候，所有的结点都是森林中的一棵树，因此权重最下的边必然是最小生成树的一条边，故图中的边$(h,g)\in A$，然后将结点$h、g$所在的两棵树合并为一棵树。通过从小到大的顺序遍历图中的所有边，最终森林中的所有树会合并为一棵树，即我们要的最小生成树$T$。

为了实现上述算法，首先确定用来表示图$G=(V,E)$的数据结构。

从伪代码可以看出，图$G$中需要有结点的集合$G.V$和边的集合$G.E$，由于我们不需要通过结点来查找边，因此不需要用邻接链表或邻接矩阵表示图。

为了简化程序，这里不打算用多个集合来表示算法运行中的树，而是在结点$v$中用属性set来表示其所属集合。因此，结点和边的数据结构如下：

struct vertex {
	char name; // vertex name
	int set; // set
};
struct edge {
	vertex* u; // vertex 1
	vertex* v; // vertex 2
	int weight = 0; // weight
};

因此，Kruskal算法的关键代码如下，完整代码见附录：

int MST::frustal() {
	int mst = 0;
	list<edge* > A;
	for (int i = 0; i < V.size(); i++) {
		V[i].set = i;
	}
	sort(E.begin(), E.end());
	for (edge& e : E) {
		if (e.u->set != e.v->set) {
			A.push_back(&e);
			unionSet(e.u->set, e.v->set);
			mst += e.weight;
		}
	}
	return mst;
}

4. Prim 算法

Prim算法与Kruskal算法类似，不过Prim算法仅将所有结点分为两个集合S和V-S，也就是最小生成树的子集中的结点和剩下的所有结点两类。

算法的每一步在连接集合S和S之外的结点的所有边中，选择一条轻量级边加入到A中，根据前文中的推论，这条规则所加入的边都是对A安全的边。因此，当算法终止时，A中的边形成一棵最小生成树。下图展示了Prim算法的贪心选择策略：

上图中，蓝色的边表示A中的边；红色的边表示连接集合S中的结点和剩余结点的边，也即当前贪心选择的候选边。Prim算法每一次做出的贪心选择就是选择上图中红色边中权值最小的边(u, v)并判断其端点$u、v$是否属于同一集合。

Prim算法的伪代码如下：

MST_PRIM(G, w, r)
	Q = ∅
	A = ∅
	for each u ∈ G.V
		u.set = 0
	r.set = 1
	for each e ∈ G.Adj[r]
		Q.push(e)
	while Q ≠ ∅
		e = EXTRACT_MIN(Q)
		if e.u.set ≠ e.v.set
			A.push(e)
			for each ev ∈ G.adj[e.v]
				if ev.v ≠ e.u
					Q.push(ev)	
			e.v.set = 1
	return A

在伪代码中，为了更快的找到当前候选边中权值最小的边，维护了一个用于保存候选边的优先队列Q。

Prim算法的运行过程如下：

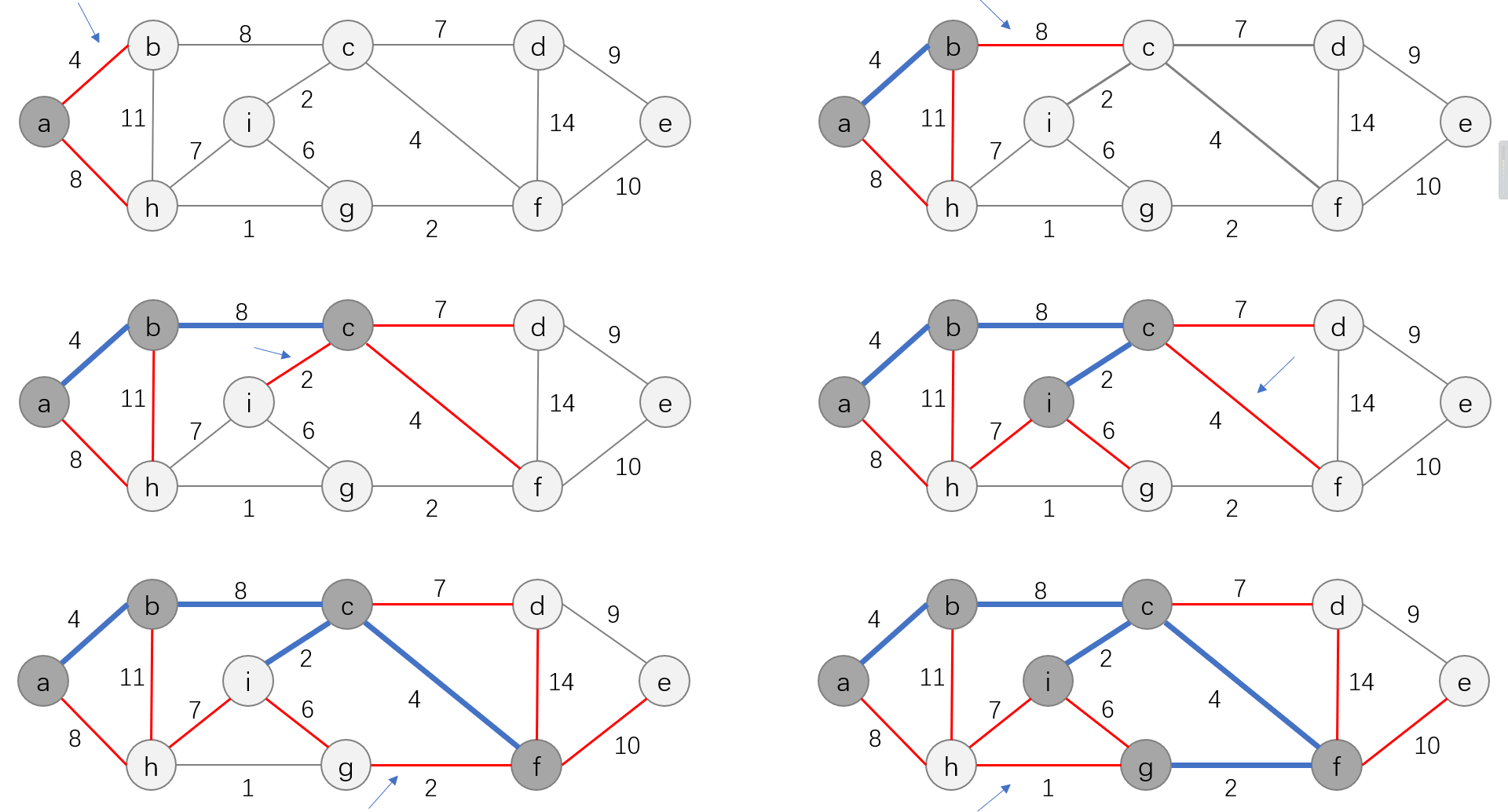
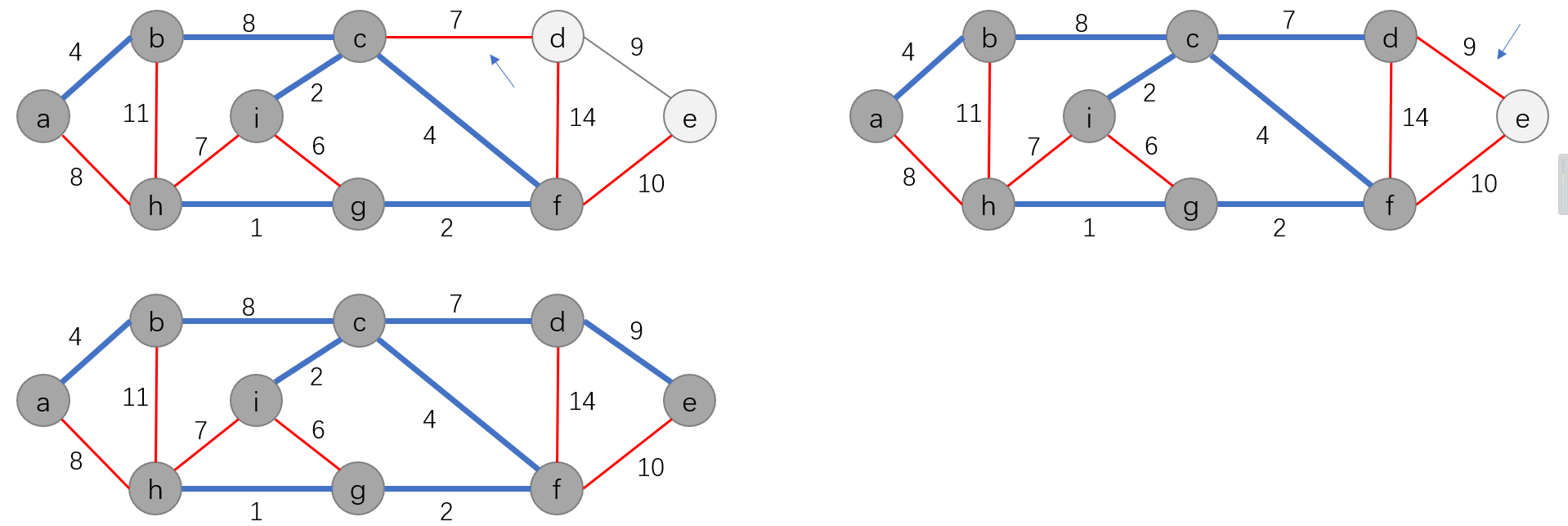
在Prim算法中，每次迭代会访问当前结点相关联的边，因此这里使用了邻接链表$G.Adj$来存储图$G$。

Prim算法的关键代码如下：

int MST::prim(char rc) {
	int mst = 0;
	vector<edge> A;
	priority_queue<edge> Q;
	vertex* r = find(rc);
	for (edge e : Adj[rc]) {
		Q.push(e);
	}
	r->set = S;
	while (!Q.empty()) {
		edge e = Q.top(); Q.pop();
		if (e.u->set != e.v->set) {
			A.push_back(e);
			mst += e.weight;
			for (edge ev : Adj[e.v->name]) {
				if(ev.v != e.u)
					Q.push(ev);
			}
			e.v->set = S;
		}
	}
	return mst;
}

5. 附录（代码）

5.1 Kruskal 算法代码

#include <iostream>
#include <vector>
#include <list>
#include <utility>
#include <queue>
using namespace std;
struct vertex {
	char name; // vertex name
	int set; // set
};
struct edge {
	vertex* u;
	vertex* v;
	int weight = 0;
};
bool operator<(const edge& A, const edge& B) {
	return A.weight < B.weight;
}

class MST{
private:
	vector<vertex> V;
	vector<edge> E;
	vertex* find(char ch) {
		// find vertex by name
		for (vertex& v : V) {
			if (ch == v.name) return &v;
		}
	}
	void unionSet(int set1, int set2) {
		for (vertex& v : V) {
			if (v.set == set1) v.set = set2;
		}
	}
public:
	void graph_init(vector<char> vData, vector<pair<pair<char, char>, int>> eData);
	int frustal();
};
void  MST::graph_init(vector<char> vData, vector<pair<pair<char, char>, int>> eData) {
	// graph initialization
	int n = vData.size();
	// save vertex
	for (int i = 0; i < n; i++) {
		vertex* p = new vertex{ vData[i], i}; // new vertex
		V.push_back(*p);
	}
	// save edge
	for (auto e : eData) {
		E.push_back(edge{ find(e.first.first), find(e.first.second), e.second });
	}

}
int MST::frustal() {
	int mst = 0;
	list<edge* > A;
	for (int i = 0; i < V.size(); i++) {
		V[i].set = i;
	}
	sort(E.begin(), E.end());
	for (edge& e : E) {
		if (e.u->set != e.v->set) {
			A.push_back(&e);
			unionSet(e.u->set, e.v->set);
			mst += e.weight;
		}
	}
	return mst;
}
int main(int argc, char* argv[]) {
	vector<char> V = { 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i' };
	vector<pair<pair<char, char>, int>> E = { {{'a', 'b'}, 4} ,{{'a', 'h'}, 8} ,{{'b', 'h'}, 11} ,{{'b', 'c'}, 8},
											  {{'h', 'i'}, 7} ,{{'h', 'g'}, 1} ,{{'i', 'c'}, 2} ,{{'i', 'g'}, 6},
											  {{'c', 'd'}, 7} ,{{'c', 'f'}, 4} ,{{'g', 'f'}, 2} ,{{'d', 'f'}, 14},
											  {{'d', 'e'}, 9} ,{{'f', 'e'}, 10} };
	MST mst;
	mst.graph_init(V, E);
	cout << mst.frustal();
	return 0;
}

5.2 Prim 算法代码

#include <iostream>
#include <vector>
#include <list>
#include <utility>
#include <unordered_map>
#include <queue>
using namespace std;
enum SET{S, V_S};
struct vertex {
	char name; // vertex name
	SET set = V_S; // set
};
struct edge {
	vertex* u;
	vertex* v;
	int weight = 0;
};
bool operator<(const edge& A, const edge& B) {
	return A.weight > B.weight;
}

class MST {
private:
	vector<vertex> V;
	unordered_map<char,list<edge>> Adj;
	vertex* find(char ch) {
		// find vertex by name
		for (vertex& v : V) {
			if (ch == v.name) return &v;
		}
		return nullptr;
	}
public:
	void graph_init(vector<char> vData, vector<pair<pair<char, char>, int>> eData);
	int prim(char r);
};
void  MST::graph_init(vector<char> vData, vector<pair<pair<char, char>, int>> eData) {
	// graph initialization
	int n = vData.size();
	// save vertex
	for (int i = 0; i < n; i++) {
		vertex* p = new vertex{ vData[i], V_S }; // new vertex
		V.push_back(*p);
	}
	// save edge
	for (auto e : eData) {
		Adj[e.first.first].push_back(edge{ find(e.first.first), find(e.first.second), e.second });
		Adj[e.first.second].push_back(edge{ find(e.first.second), find(e.first.first), e.second });
	}
}
int MST::prim(char rc) {
	int mst = 0;
	vector<edge> A;
	priority_queue<edge> Q;
	vertex* r = find(rc);
	for (edge e : Adj[rc]) {
		Q.push(e);
	}
	r->set = S;
	while (!Q.empty()) {
		edge e = Q.top(); Q.pop();
		if (e.u->set != e.v->set) {
			A.push_back(e);
			mst += e.weight;
			for (edge ev : Adj[e.v->name]) {
				if(ev.v != e.u)
					Q.push(ev);
			}
			e.v->set = S;
		}
	}
	return mst;
}
int main(int argc, char* argv[]) {
	vector<char> V = { 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i' };
	vector<pair<pair<char, char>, int>> E = { {{'a', 'b'}, 4} ,{{'a', 'h'}, 8} ,{{'b', 'h'}, 11} ,{{'b', 'c'}, 8},
											  {{'h', 'i'}, 7} ,{{'h', 'g'}, 1} ,{{'i', 'c'}, 2} ,{{'i', 'g'}, 6},
											  {{'c', 'd'}, 7} ,{{'c', 'f'}, 4} ,{{'g', 'f'}, 2} ,{{'d', 'f'}, 14},
											  {{'d', 'e'}, 9} ,{{'f', 'e'}, 10} };
	MST mst;
	mst.graph_init(V, E);
	cout << mst.prim('a');
	return 0;
}