【算法导论-贪心算法】贪心算法原理和理论以及多个实例和变形(附有代码和简单实现)

参考网址：贪心算法
参考书籍：《算法导论》

前言：

求解最优化问题的算法通常需要经过一系列的步骤，在每个步骤都面临多种选择。对于许多最优化问题，使用动态规划算法来求最优解有些杀鸡用牛刀了，可以使用更简单、更高效的算法。贪心算法(greedyalgorithm)就是这样的算法，它在每一步都做出当时看起来最佳的选择。也就是说，它总是做出局部最优的选择，寄希望这样的选择能导致全局最优解。贪心算法并不保证得到最优解，但对很多问题确实可以求得最优解。
贪心算法只需考虑一个选择（即贪心的选择），在做贪心选择时，子问题之一必是空的，因此，只留下一个非空子问题。基千这些观察，我们将找到一种递归贪心算法来解决活动调度问题，并将递归算法转化为迭代算法，以完成贪心方法的过程。它们说明了贪心算法和动态规划之间 的关系。

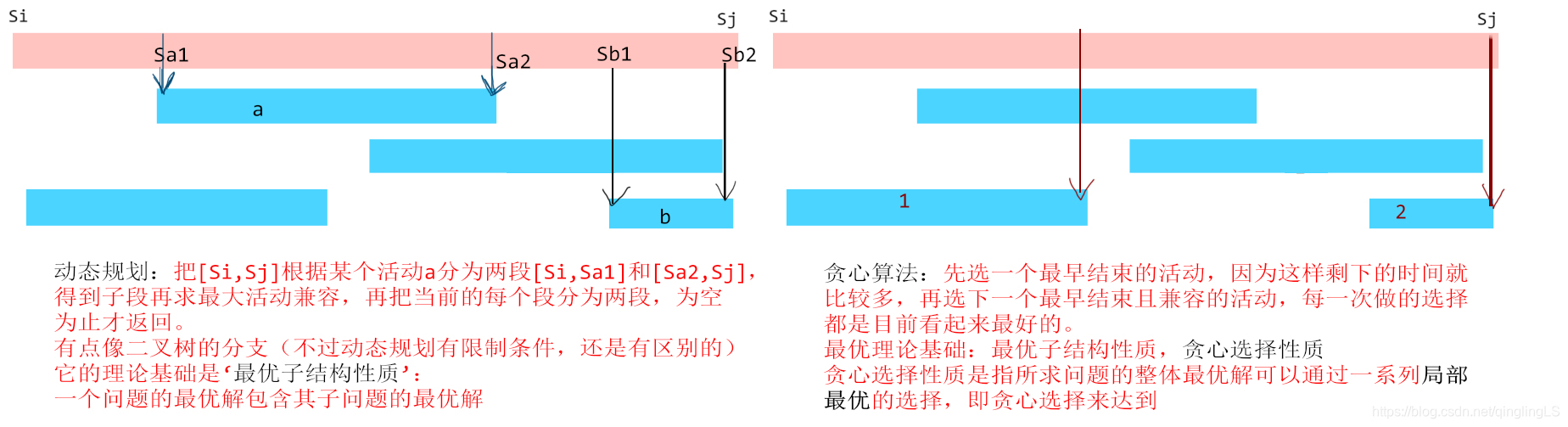
可以用贪心算法求解的问题中看到这类问题一般具有2个重要的性质：贪心选择性质和最优子结构性质。

1、贪心选择性质

所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。
这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。
动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常以自顶向下的方式进行，以迭代的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为规模更小的子问题。
对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。

2、最优子结构性质

当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。

3、贪心算法与动态规划算法的差异

贪心算法和动态规划算法都要求问题具有最优子结构性质，这是2类算法的一个共同点。
但是，对于具有最优子结构的问题应该选用贪心算法还是动态规划算法求解?是否能用动态规划算法求解的问题也能用贪心算法求解?这个后面说。

经典例1、活动安排问题：

设有$n$个活动的集合$E=1,2,\dots ,n$，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。每个活动 $Ei$ 都有一个要求使用该资源的起始时间$si$和一个结束时间$fi$ ,且$si<fi$ 。如果选择了活动i，则它在半开时间区间$[si,fi)$内占用资源。
若区间$[si,fi)$与区间$[sj,fj)$不相交，则称活动i与活动j是相容的。也就是说，当$si>=fj或sj>=fi$时，活动i与活动j相容。
要安排尽量多的活动，获得最大兼容活动集（注意不是最大时间占用！只要求活动数多，举办的活动多，不要求活动室被使用时间最高效率）
待安排的活动开始结束时间如下: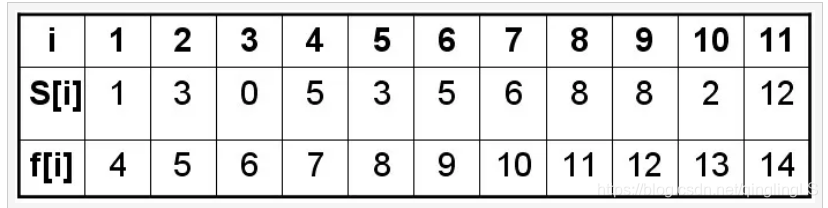

思路：

1.证明最优子结构性质：

假设$Sij$是在$ai$结束之后开始，而且在$aj$开始之前结束的那些活动的集合，假定我们希望求$Sij$的一个最大的相互兼容的活动子集，进一步假定$Aij$就是这样一个子集，$A_{ij}$一定包含至少一个活动$a_k$(如果连一个活动都不能兼容，说明这个集合无解，根本没有兼容集合)。由于最优解包含活动$a_k$,我们得到两个子问题：寻找$Sik$中的兼容活动（在$ak$结束之后开始且$ak$开始之前结束的那些活动）以及寻找$Skj$中的兼容活动（在$ak$结束之后开始且在$aj$开始之前结束的那些活动） 也就是找找那些未被活动$a_k$占用的时间是否还可以兼容活动

所以 A i j = A i k ∪ { a k } ∪ A k j A_{ij}=A_{ik} \cup \{ak\}\cup A_{kj} Aij​=Aik​∪{ ak}∪Akj​

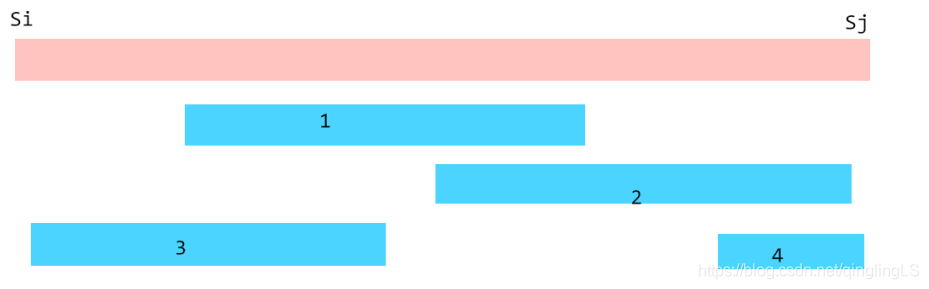
例如图中可看出 { 1 , 4 } , { 3 , 2 } , { 3 , 4 } \{1,4\},\{3,2\},\{3,4\} { 1,4},{ 3,2},{ 3,4}兼容，
如果初始的活动是
$a_{}$