python 关于基础矩阵的图像处理

（一）基本原理

本篇原理部分转载参考自以下两篇博文：
（1）https://www.cnblogs.com/wangguchangqing/p/8214032.html
（2）https://blog.youkuaiyun.com/kokerf/article/details/72191054

1. 本次测验目的：计算图像对的特征匹配，并估计基础矩阵。使用外极线作为第二个输入，通过在外极线上对每个特征点寻找最佳的匹配来找到更多的匹配。

2. 外极几何：
   
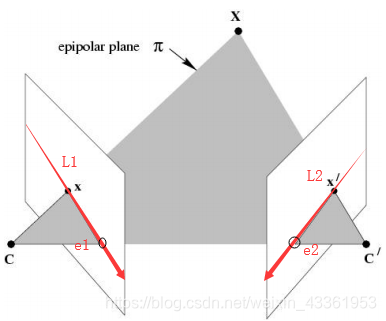
   上图为外极几何示意图，在这两个视图中，分别讲三维点X投影为x和x’，两个照相机中心之间的基线c和c’ 与图像平面相交于外极点e1和e2，L1和L2称为外极线（下文写为 l 和 l’）。

3. 本质矩阵
   （1）本质矩阵是归一化图像坐标下的基础矩阵的特殊情况。基础矩阵把要求标定相机这样一个（非本质的）的基本假设去掉了。本质矩阵描述了空间中的点在两个坐标系中的坐标对应关系。
   （2）推导：
   
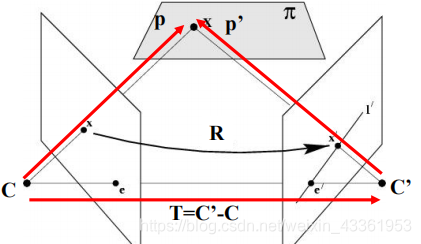
   设X在C，C’坐标系中的相对坐标分别p，p’，则有
   
   
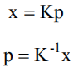
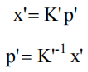
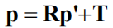
   则根据三线共面，有
   
   
   （3）性质：本质矩阵只有5个自由度：旋转矩阵R和平移矢量t各有3个自由度，由于是齐次矩阵再减去一个自由度。

4. 基础矩阵
   （1）基础矩阵 F 可以由两照相机的参数矩阵（相对旋转 R 和平移 t）表示，我们可以借助 F 来恢复出照相机参数，而 F 可以从对应的投影图像点计算出来，它体现了两视图几何（对极几何）的内在射影几何关系即基础矩阵描述了空间中的点在两个像平面中的坐标对应关系。
   （2）推导：
   根据前述， K 和 K’ 分别为两个相机的内参矩阵，有：
   
   （3）性质：假设两幅图像由中心不重合的相机获得，则基本矩阵F为所对应点x↔x′都满足下式的秩为2的3×3齐次线性矩阵：