给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。

class Solution {
List<Integer> path=new ArrayList<>();
List<List<Integer>> res=new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
int []used=new int[nums.length];
Arrays.fill(used,0);
Arrays.sort(nums);
backTrack(nums,used);
return res;
}
private void backTrack(int []nums,int[]used){
if(path.size()==nums.length){
res.add(new ArrayList<>(path));
return;
}
for(int i=0;i<nums.length;i++){
if(i>0&&nums[i]==nums[i-1]&&used[i-1]==0){
continue;
}
if(used[i]==0){
used[i]=1;
path.add(nums[i]);
backTrack(nums,used);
path.remove(path.size()-1);
used[i]=0;
}
}
}
}
为了观察回溯的过程,我在IDEA里面跑了一下,这样可以更加直观清楚的看到整个程序的运行思路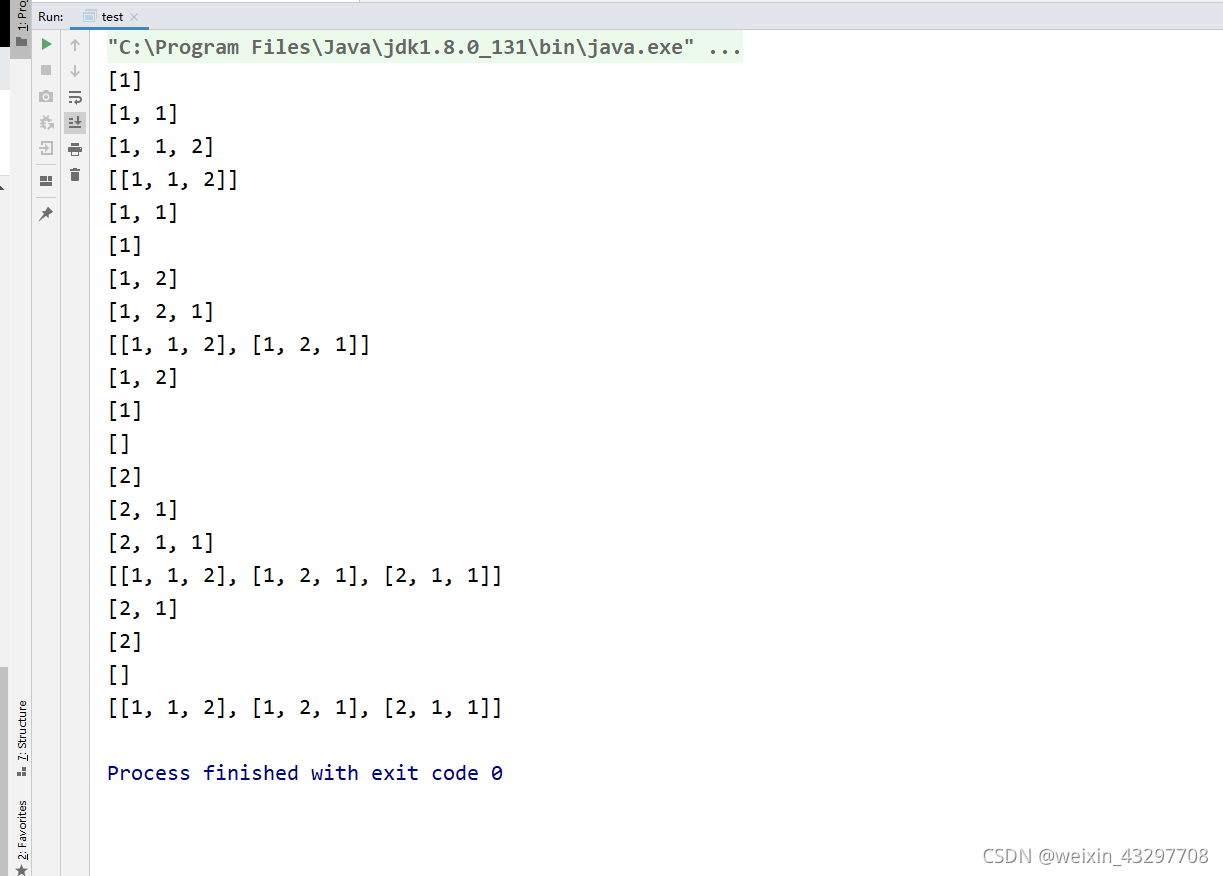




















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








