针孔相机模型

针孔相机模型就如同上图,总共包含四个坐标系,世界坐标系、相机坐标系、物理成像坐标系、像素平面坐标系。我们要理解的是这几个坐标系之间的转换。
我们看到在实际中我们的成像平面和像素平面是在光心之后的,通过针孔成像模型可以知道,得出来的像是倒像,但是我们日常用相机拍摄的时候,得出的都是正像,这是因为相机内部帮我们进行了处理,也就相当于把物理成像平面和像素平面前移到光心前了,所以我们通常看到的相机模型是这样的

像平面被移到了前面,从图中一个星点进行投影成像,在前移后的像平面下会出现其正像,由各个坐标系的轴和星点可以在像平面构成三角形
Δ
X
Y
Z
\Delta XYZ
ΔXYZ在世界坐标系构成三角形
Δ
X
c
Y
c
Z
c
\Delta X_cY_cZ_c
ΔXcYcZc其中这三角形是相似的,则
X
c
X
=
Y
c
Y
\frac{X_c}{X}=\frac{Y_c}{Y}
XXc=YYc
同时再根据另一个三角形相似
Z
c
f
=
Y
c
Y
\frac{Z_c}{f}=\frac{Y_c}{Y}
fZc=YYc
这样就可以联系起来了,注意这里的XY是成像平面上的坐标,单位还是米,不是像素坐标
X
=
f
X
c
Z
c
X=f\frac{X_c}{Z_c}
X=fZcXc
Y
=
f
Y
c
Z
c
Y=f\frac{Y_c}{Z_c}
Y=fZcYc
写成矩阵的形式
(
X
Y
1
)
=
(
f
0
0
0
0
f
0
0
0
0
1
0
)
(
R
t
0
1
)
(
X
Y
Z
1
)
\begin{pmatrix} X \\ Y \\ 1 \end{pmatrix}=\begin{pmatrix} f &0&0&0 \\ 0&f&0&0 \\ 0&0&1&0 \end{pmatrix} \begin{pmatrix} R&t \\ 0&1 \end{pmatrix}\begin{pmatrix} X \\ Y \\ Z\\ 1 \end{pmatrix}
⎝⎛XY1⎠⎞=⎝⎛f000f0001000⎠⎞(R0t1)⎝⎜⎜⎛XYZ1⎠⎟⎟⎞
- 如何将成像平面转化到像素平面
这要考虑从米的单位转换到像素平面,要注意以下几点
- 图像中的像素是有长和宽的小矩形(可以是正方形,长方形)
- 假设 d x dx dx表示每一个像素的长 d y dy dy表示每一个像素的宽(高),单位是米
- 那么 1 d x \frac{1}{dx} dx1表示一米长有几个像素,同理 1 d y \frac{1}{dy} dy1表示一米宽有几个像素
- 设 1 d x = α \frac{1}{dx}=\alpha dx1=α 1 d y = β \frac{1}{dy}=\beta dy1=β,这分别表示在X轴和Y轴上的缩放值,单位是(像素/米)
- 像素坐标和成像平面坐标系的原点是不重合的,像素坐标原点基于成像平面原点平移了
[
c
x
,
c
y
]
\left[ c_x,c_y \right]
[cx,cy]单位是像素
可以参考
那么像素坐标可以由:
( u v 1 ) = ( 1 d x 0 c x 0 1 d y c y 0 0 1 ) ( f 0 0 0 0 f 0 0 0 0 1 0 ) ( R t 0 1 ) ( X Y Z 1 ) \begin{pmatrix} u \\ v \\ 1 \end{pmatrix}=\begin{pmatrix} \frac{1}{dx} &0&c_x \\ 0&\frac{1}{dy}&c_y \\ 0&0&1 \end{pmatrix} \begin{pmatrix} f &0&0&0 \\ 0&f&0&0 \\ 0&0&1&0 \end{pmatrix} \begin{pmatrix} R&t \\ 0&1 \end{pmatrix}\begin{pmatrix} X \\ Y \\ Z\\ 1 \end{pmatrix} ⎝⎛uv1⎠⎞=⎝⎛dx1000dy10cxcy1⎠⎞⎝⎛f000f0001000⎠⎞(R0t1)⎝⎜⎜⎛XYZ1⎠⎟⎟⎞
由上式的转换之后可以得到像素坐标,单位是像素
其中 f x f_x fx f y f_y fy分别是x轴y轴上焦距的缩放,也称为焦距,当 f x = f y f_x=f_y fx=fy的时候可以理解为一个像素的长宽是相等的,是一个正方形。
- 归一化平面
归一化平面是在相机前面z=1出的平面上,在相机坐标系上进行归一化处理后才可以乘上内参矩阵转变为像素坐标
畸变
在摄像头加入了透镜后,对成像过程光线的传播产生新的影响:一是透镜本身的形状,会产生轻微折射(径向畸变);二是机械组装的时候透镜和成像平面不可能完全平行(切向畸变);这都会造成光线穿过透镜投影到的成像平面时和理想的针孔成像模型的成像位置发生变化
 我们看到图像,明明现实场景中是直线,但是在相片中就弯曲了
我们看到图像,明明现实场景中是直线,但是在相片中就弯曲了

发现一些形状边缘出现了弯曲,其实我们可以通过畸变系数找到各个点的在像素平面的位置

其中k1.k2.k3.p1.p2这些都是相机的内参,是可以通过相机的标定得到,
r
2
=
x
2
+
y
2
r^2=x^2+y^2
r2=x2+y2,值得注意的是,x、y都是归一化平面上的坐标,已经除上了Z坐标值
例题,不使用opencv的去畸变函数,直接用上面的去畸变方程,处理上面图像的畸变,并显示
//
// Created by 高翔 on 2017/12/15.
//
#include <opencv2/opencv.hpp>
#include <string>
using namespace std;
string image_file = "./test.png"; // 请确保路径正确
int main(int argc, char **argv) {
// 本程序需要你自己实现去畸变部分的代码。尽管我们可以调用OpenCV的去畸变,但自己实现一遍有助于理解。
// 畸变参数
double k1 = -0.28340811, k2 = 0.07395907, p1 = 0.00019359, p2 = 1.76187114e-05;
// 内参
double fx = 458.654, fy = 457.296, cx = 367.215, cy = 248.375;
cv::Mat image = cv::imread(image_file,0); // 图像是灰度图,CV_8UC1
int rows = image.rows, cols = image.cols;
cv::Mat image_undistort = cv::Mat(rows, cols, CV_8UC1); // 去畸变以后的图
// 计算去畸变后图像的内容
for (int v = 0; v < rows; v++)
for (int u = 0; u < cols; u++) {
double u_distorted = 0, v_distorted = 0;
// TODO 按照公式,计算点(u,v)对应到畸变图像中的坐标(u_distorted, v_distorted) (~6 lines)
// start your code here
double x=(u-cx)/fx;
double y=(v-cy)/fy;
double r2=x*x+y*y;
double x_distorted=x*(1+k1*r2+k2*r2*r2)+2*p1*x*y+p2*(r2+2*x*x);
double y_distorted=y*(1+k1*r2+k2*r2*r2)+p1*(r2+2*y*y)+2*p2*x*y;
u_distorted=fx*x_distorted+cx;
v_distorted=fy*y_distorted+cy;
// end your code here
// 赋值 (最近邻插值)
if (u_distorted >= 0 && v_distorted >= 0 && u_distorted < cols && v_distorted < rows) {
image_undistort.at<uchar>(v, u) = image.at<uchar>((int) v_distorted, (int) u_distorted);
} else {
image_undistort.at<uchar>(v, u) = 0;
}
}
// 画图去畸变后图像
cv::imshow("image undistorted", image_undistort);
cv::waitKey();
return 0;
}
结果显示

发现物体边缘部分是变直了些
双目成像
仅靠一张图片是无法知道任何一个特征点的深度信息,也就是相机坐标系中的Z坐标,两张图像就可以通过三角形关系,同意特征点知道两图像中的成像视差(左右图横坐标之差),利用三角形相似,求出点的深度信息
具体的推导过程可以参考我之前写过的博客
例题,给出一组双目相机的成像图,和对应的视差图,求出每个点的深度,得出点云
//
// Created by 高翔 on 2017/12/15.
//
#include <opencv2/opencv.hpp>
#include <string>
#include <Eigen/Core>
#include <pangolin/pangolin.h>
#include <unistd.h>
using namespace std;
using namespace Eigen;
// 文件路径,如果不对,请调整
string left_file = "./left.png";
string right_file = "./right.png";
string disparity_file = "./disparity.png";
// 在panglin中画图,已写好,无需调整
void showPointCloud(const vector<Vector4d, Eigen::aligned_allocator<Vector4d>> &pointcloud);
int main(int argc, char **argv) {
// 内参
double fx = 718.856, fy = 718.856, cx = 607.1928, cy = 185.2157;
// 间距
double d = 0.573;
// 读取图像
cv::Mat left = cv::imread(left_file, 0);
cv::Mat right = cv::imread(right_file, 0);
cv::Mat disparity = cv::imread(disparity_file,0); // disparty 为CV_8U,单位为像素
// 生成点云
vector<Vector4d, Eigen::aligned_allocator<Vector4d>> pointcloud;
// TODO 根据双目模型计算点云
// 如果你的机器慢,请把后面的v++和u++改成v+=2, u+=2
for (int v = 0; v < left.rows; v++)
for (int u = 0; u < left.cols; u++) {
Vector4d point(0, 0, 0, left.at<uchar>(v, u) / 255.0); // 前三维为xyz,第四维为颜色
// start your code here (~6 lines)
// 根据双目模型计算 point 的位置
//uchar disp = disparity.ptr<uchar>(v)[u];
//不知道为什么一定要用ptr指针来进行读取
unsigned int disp=disparity.ptr<unsigned short>(v)[u];
//uchar *disp1=disparity.ptr<uchar>(v);
// float disp=disparity.at<float>(v,u);
//uchar disp=disparity.at<uchar>(v,u);
if(disp==0) continue;
point[2]=fx*d*1000/disp;
point[0]=(u-cx)*point[2]/fx;
point[1]=(v-cy)*point[2]/fy;
pointcloud.push_back(point);
// end your code here
}
// 画出点云
showPointCloud(pointcloud);
return 0;
}
void showPointCloud(const vector<Vector4d, Eigen::aligned_allocator<Vector4d>> &pointcloud) {
if (pointcloud.empty()) {
cerr << "Point cloud is empty!" << endl;
return;
}
pangolin::CreateWindowAndBind("Point Cloud Viewer", 1024, 768);
glEnable(GL_DEPTH_TEST);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
pangolin::OpenGlRenderState s_cam(
pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
);
pangolin::View &d_cam = pangolin::CreateDisplay()
.SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
.SetHandler(new pangolin::Handler3D(s_cam));
while (pangolin::ShouldQuit() == false) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
d_cam.Activate(s_cam);
glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
glPointSize(2);
glBegin(GL_POINTS);
for (auto &p: pointcloud) {
glColor3f(p[3], p[3], p[3]);
glVertex3d(p[0], p[1], p[2]);
}
glEnd();
pangolin::FinishFrame();
usleep(5000); // sleep 5 ms
}
return;
}
结果显示
 可以看到出现了层次的效果
可以看到出现了层次的效果
鱼眼相机、全景相机
鱼眼相机
鱼眼相机是指带有鱼眼镜头的相机,是一种焦距极短并且视角接近或等于180°的镜头。16mm或焦距更短的镜头。 它是一种极端的广角镜头,“鱼眼镜头”是它的俗称。
鱼眼相机为了增加广角,镜头的原因,会造成镜像畸变,产生桶形失真,鱼眼镜头最大的作用是视角范围大,视角一般可达到220°或230°

全景相机
全景相机其内部封装多个不同朝向的传感器,通过对分画面进行图像拼接操作得到全景效果。主流产品的结构是把若干两百万图像的传感器,以及视场角独立短焦镜头封装在统一的外壳中
而随着摄像头、处理器和传感器技术的不断发展,360 度全景相机只需要一两颗鱼眼镜头就可以实现

这是由前后两个鱼眼相机组成的全景相机

这是拍出来的效果
全局快门和卷帘宽门相机
常见的电子快门的方式有Global shutter(全局快门) 和 rolling shutter(卷帘式快门)两种,全局快门是通过整幅图片在同一时间曝光实现的。传感器的所有像素点同时收集光线,同时曝光。当预设的曝光时间到了,传感器停止收集光线,并将曝光图像转成电子图像。在这个过程中,并没有实际意义上的快门存在。在曝光开始的时候,传感器开始收集光线;在曝光结束的时候,光线收集电路被切断,传感器读出值即为一副图片。
卷帘式快门与全局快门不同,它是通过控制芯片逐行曝光的方式实现的。卷帘式快门也没有实际意义上的快门,而是通过通断电控制传感器,使其不同部分在不同时间下对光的敏感度不同。逐行进行曝光,直至所有像素点都被曝光。当然,所有的动作在很短的时间内完成,一般情况为1/48至1/60秒。需要注意的是,卷帘式快门采用的是逐行曝光的方式。假如物体或摄像头在拍摄期间处于快速运动状态,拍摄结果就可能出现“倾斜”、“摇摆不定”或“部分曝光”等任一种情况。
卷帘式快门是逐行顺序曝光,所以不适合运动物体的拍摄。当采用全局快门方式曝光时,所有像素在同一时刻曝光,类似于将运动物体冻结了,所以适合拍摄快速运动的物体。但是全局快门可能出现像糊现象。像糊现象出现与否取决于曝光时间的长短。假如曝光时间过长,且物体运动过快则会出现像糊;假如曝光时间很短,类似于运动物体在瞬间被冻结了,则少有像糊。

图像曝光和读取数据的区别
卷帘快门逐行曝光,在逐行读取,未读到的数据可能会随时间变化
全局快门全部行同时曝光,数据被固定,直至数据被读取完毕

运动图像效果对比
当出现高速运动后,卷帘相机会出现明显的“果冻效应”,如左图所示。右图展示的全局相机的拍摄结果,可以发现虽然仍然出现了模糊问题,但是并没有出现果冻问题

卷帘快门在SLAM中拍摄运动物体很可能造成前后帧匹配对应不上,出现丢失或者误匹配,影响系统的稳定性和精度
一般情况下SLAM中为了避免运动物体对整个系统产生较大影响,一般都会采用全局快门相机,其缺点是价格昂贵
三种方法遍历图像
OpenCV中常用的遍历图像的方法主要有三中,包括基于at,ptr和迭代器的方法,实验结果是是ptr的效果最佳
#include <iostream>
#include <ctime>
#include <opencv2/opencv.hpp>
int main()
{
// Mat
//cv::Mat image =cv::Mat::zeros(1000, 1000, CV_8UC3);
cv::Mat image = cv::imread("./test.png");//按照原图读入,否则下面对像素值修改时会现段错误出错
cv::imshow("initial",image);
cv::waitKey();
cv::Mat image1=image.clone();
// By at
clock_t atBegin = clock();
for (int y = 0; y < image1.rows; y++)
{
for (int x = 0; x < image1.cols; x++)
{
image1.at<cv::Vec3b>(y,x) = cv::Vec3b(100, 100, 100);
}
}
clock_t atFinish = clock();
std::cout << "Time: " << (atFinish - atBegin)*1.0 / CLOCKS_PER_SEC << std::endl;
cv::imshow("aa",image1);
cv::waitKey(0);
// By ptr
cv::Mat image2=image.clone();
clock_t ptrBegin = clock();
for (int y = 0; y < image2.rows; y++)
{
for (int x = 0; x < image2.cols; x++)
{
image2.ptr<cv::Vec3b>(y)[x]= cv::Vec3b(100, 100, 100);
}
}
clock_t ptrFinish = clock();
std::cout << "Time: " << (ptrFinish - ptrBegin)*1.0 / CLOCKS_PER_SEC << std::endl;
cv::imshow("bb",image2);
cv::waitKey(0);
// By Iterator
cv::Mat image3=image.clone();
clock_t iteratorBegin = clock();
cv::Mat_<cv::Vec3b>::iterator begin = image3.begin<cv::Vec3b>();
cv::Mat_<cv::Vec3b>::iterator end = image3.end<cv::Vec3b>();
for (; begin != end; begin++)
{
(*begin) = cv::Vec3b(100, 100, 100);
}
clock_t iteratorFinish = clock();
std::cout << "Time: " << (iteratorFinish - iteratorBegin)*1.0 / CLOCKS_PER_SEC << std::endl;
cv::imshow("cc",image3);
cv::waitKey(0);
return 0;
}
结果


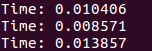
可以看到,遍历是ptr指针效率最高

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








