diffusion原理推导

diffusion原理推导

sd3：图像经过vae的encoder，采样成latent feature（高斯分布），作为原始feature。unet作为diffusion的主要模块，输入是不同阶段的图像feature 、 噪声和时间步，预测的是噪声。去噪是通过后一时刻的图像feature一步步减去预测的噪声，恢复到原来的图像feature，然后通过vae的decoder恢复成原始图像。

总结：diffusion的前向加噪过程是由慢到快地改变原始图像，最后符合一个01的高斯分布。反向去噪的过程是通过一个神经网络通过后一时刻的相关的μ_t​和方差β_​t得到t-1时刻的分布。训练过程随机预测T时刻中的某一个时刻，随机生成一个标准正态分布的噪声$ϵ$生成加噪图像，再送进预测噪声的神经网络中。
diffusion是一种特殊的vae，加噪声作为编码过程，去噪声作为解码过程，latent-feature一直都是图片，细节损失较少，生成的图像质量高；优化的目标也是最大似然，训练比较稳定。
https://segmentfault.com/a/1190000043744225
https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
1、前向加噪
准确来说，加噪不是给上一时刻的图像加上噪声值，而是从一个均值与上一时刻图像相关的正态分布里采样出一幅新图像。

xt​可以通过一个标准正态分布的样本ϵt−1​算出来

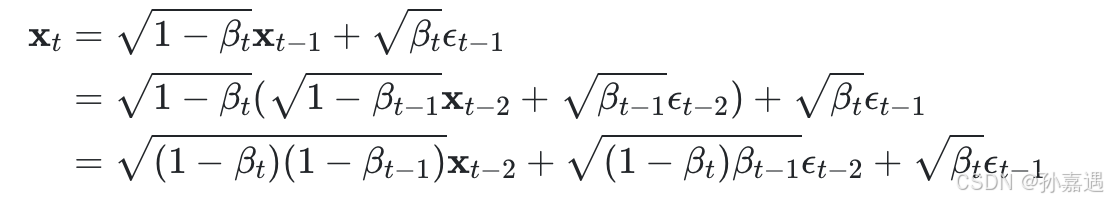
根据正态分布和的性质，后两项的方差合在一起

递推到x_0: β_t​从β_1=10^(−4)到β_T​=0.02线性增长。这样，β_t​变大，α_t​也越小，α_t​趋于0的速度越来越快。
加噪声公式能够从慢到快地改变原图像，让图像最终均值为0，方差为I。

2、反向去噪
加噪声的逆操作，通过网络去拟合这个相关（后一时刻）的μ_t​和方差β_​t。

在x_0样本下，利用多条件贝叶斯公式

求解出来x_{t-1}的分布：

神经网络拟合均值时，x_t​是已知的，式子里唯一不确定的只有ϵ_t​。既然如此，神经网络不预测均值，直接预测一个噪声ϵ_θ​(x_t​,t)（其中θ为可学习参数），让它和生成x_t​的噪声ϵ_t​的均方误差最小。

3、训练算法和采样

为什么最后一步的z=0呢？