POJ 2516 Minimum Cost(最小费用最大流)

POJ 2516 Minimum Cost(最小费用最大流)

Dearboy, a goods victualer, now comes to a big problem, and he needs your help. In his sale area there are N shopkeepers (marked from 1 to N) which stocks goods from him.Dearboy has M supply places (marked from 1 to M), each provides K different kinds of goods (marked from 1 to K). Once shopkeepers order goods, Dearboy should arrange which supply place provide how much amount of goods to shopkeepers to cut down the total cost of transport.

It’s known that the cost to transport one unit goods for different kinds from different supply places to different shopkeepers may be different. Given each supply places’ storage of K kinds of goods, N shopkeepers’ order of K kinds of goods and the cost to transport goods for different kinds from different supply places to different shopkeepers, you should tell how to arrange the goods supply to minimize the total cost of transport.
Input
The input consists of multiple test cases. The first line of each test case contains three integers N, M, K (0 < N, M, K < 50), which are described above. The next N lines give the shopkeepers’ orders, with each line containing K integers (there integers are belong to [0, 3]), which represents the amount of goods each shopkeeper needs. The next M lines give the supply places’ storage, with each line containing K integers (there integers are also belong to [0, 3]), which represents the amount of goods stored in that supply place.

Then come K integer matrices (each with the size N * M), the integer (this integer is belong to (0, 100)) at the i-th row, j-th column in the k-th matrix represents the cost to transport one unit of k-th goods from the j-th supply place to the i-th shopkeeper.

The input is terminated with three "0"s. This test case should not be processed.
Output
For each test case, if Dearboy can satisfy all the needs of all the shopkeepers, print in one line an integer, which is the minimum cost; otherwise just output “-1”.
Sample Input
1 3 3
1 1 1
0 1 1
1 2 2
1 0 1
1 2 3
1 1 1
2 1 1

1 1 1
3
2
20

0 0 0
Sample Output
4
-1

题目大意：

n个客户，m个仓库，l件物品。

n行l列 表示n个客户对l件物品的需求量

m行l列 表示m个仓库对l件物品的的供给量

l行 表示l个物品从i仓库到j客户的一个物品的运费价格

判断是否可以满足客户需求，如果满足求出最小的运费。

解题思路：

这个题建图一开始困难的地方就是在那k个货物上。
k个货物没法建图。我们就想把这k个货物分开来建图，一个货物建一个图，这样就好建图了。
对于每一个货物x，建立一个超级原点，连每个供货商y，流量就是y供货商有多少个货物x，花费是0。
然后对于每个商店z 我们链接超级汇点，流量是z商店对x货物的需求，花费都是0.
然后供货商 和 商店之间连边，流量可以设为inf 也可设为供货商对这个商品的拥有量。花费就是 x这个货物在这个供货商到 商店之间运送的花费。
（流量/花费）

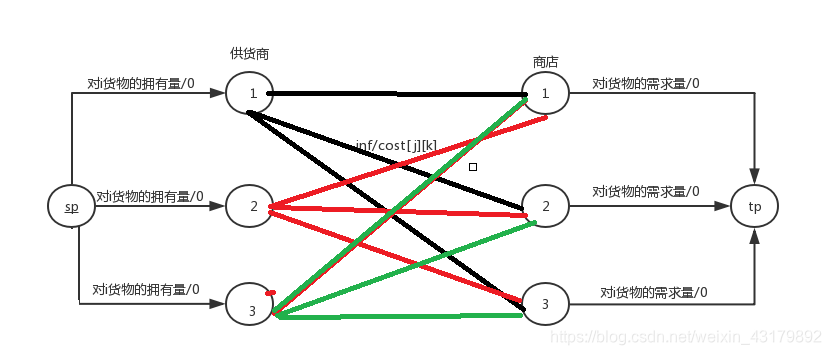
然后对每个货物 都建一次图，都跑一个最小费用流，最后加起来就是我们要的答案了
对于-1的情况，任何一个货物，只要让所有供货商的存货和所有商店的需求 比较就行

AC代码：

#include <iostream>
#include <queue>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 1e2+10;
const int maxm = 1e5+10;
struct node{
	int to;
	int cap;//流量
	int cost;//权值
	int flow;//已经流了多少流量 
	int next;
}side[maxm];
int n,m,k;
int sp,tp;
int head[maxn],cnt = 0;//建图
int dis[maxn];//最短路
int pre_point[maxn];//前驱结点
int pre_side[maxn];
int vis[maxn];
void init(){
	memset(head,-1,sizeof(head));
	cnt = 0;
}
void add(int x,int y,int cap,int cost){
	side[cnt].to = y;
	side[cnt].cap = cap;
	side[cnt].cost = cost;
	side[cnt].next = head[x];
	side[cnt].flow = 0; 
	head[x] = cnt++;

	//反向边
	side[cnt].to = x;
	side[cnt].flow = 0;
	side[cnt].cap = 0;//反向流量初始为0
	side[cnt].cost = -cost;//反向花费为负值
	side[cnt].next = head[y];
	head[y] = cnt++;
}

//用最短路的方式找增广路。找一条花费最小的增广路
bool spfa(int s,int e){
	memset(pre_side,-1,sizeof(pre_side));
	memset(pre_point,-1,sizeof(pre_point));
	memset(dis,inf,sizeof(dis));
	memset(vis,0,sizeof(vis));
	dis[s] = 0;
	vis[s] = 1;
	queue<int> q;
	q.push(s);
	while(q.size()){
		int now = q.front();
		q.pop();
		vis[now] = 0;
		for(int i = head[now];i!=-1;i=side[i].next){
			if(side[i].cap>side[i].flow){
				int to = side[i].to;
				if(dis[to]>dis[now]+side[i].cost){
					dis[to] = dis[now]+side[i].cost;
					pre_side[to] = i;//哪条边
					pre_point[to] = now;
					if(!vis[to]){
						q.push(to);
						vis[to] = 1;
					}
				}
			}	
		}
	}
	if(dis[e]==inf){//没有找到增广路
		return false;
	}else return true;
}
int min_cost_flow(int s,int e){
	int ans_flow = 0;
	int ans_cost = 0;
	int u,mn;
	while(spfa(s,e)){
		u = e;
		int f=0x3f3f3f3f;
		for(int u=pre_side[e];u!=-1;u=pre_side[side[u^1].to]){
			if(f>side[u].cap-side[u].flow)//一条增广路上的最小的流就是增广的值,cap-flow 增广的值
				f=side[u].cap-side[u].flow;
		}
		ans_flow+=f;///加到总的流量上

		for(int i=pre_side[e];i!=-1;i=pre_side[side[i^1].to]){
			side[i].flow+=f;
			side[i^1].flow -=f;
			ans_cost+=side[i].cost*f;
		}
	
	}
	return ans_cost;
}
int need[maxn][maxn];
int have[maxn][maxn];
int cost[maxn][maxn][maxn]; 
int main(){
	while(~scanf("%d%d%d",&n,&m,&k)){
		if(n==0&&m==0&&k==0) break;
		init();
		for(int i=1;i<=n;i++){
			for(int j=1;j<=k;j++)
				scanf("%d",&need[i][j]);//第i个商店对第j中货物的需求 
		} 
		for(int i=1;i<=m;i++){
			for(int j=1;j<=k;j++){
				scanf("%d",&have[i][j]);//第i个供货商拥有j货物多少个
	 
			}
		}
		for(int i=1;i<=k;i++){
			for(int j=1;j<=n;j++){
				for(int q=1;q<=m;q++){
					scanf("%d",&cost[i][j][q]);//第i个货物 从q供货商到j商店的花费 
				}
			}
		}
		
		//判断是否能够 
		int flag = 1;
		for(int i=1;i<=k;i++){
			int HAVE = 0;
			for(int j=1;j<=m;j++){
				HAVE+=have[j][i];
			} 
			int NEED = 0;
			for(int j=1;j<=n;j++){
				NEED+=need[j][i]; 
			} 
			if(NEED>HAVE){
				flag = 0;
				break;
			}
		}
		if(flag == 0){
			printf("-1\n");
			continue;
		}
		int sum = 0; 
		for(int i=1;i<=k;i++){
			init();
			sp = 1;
			tp = 1+n+m+1;
			for(int j=1;j<=m;j++){
				int hh = have[j][i];//注意是hava[j][i]不是[i][j]; 
				add(1,j+1,hh,0);
			}
			for(int j=1;j<=n;j++){
				int nn = need[j][i];
				add(1+m+j,tp,nn,0);
			}		
			int u,v;
			for(int j=1;j<=m;j++){
				int flow = have[j][i];
				u = j+1;
				for(int q=1;q<=n;q++){
					int cc = cost[i][q][j];
					v = q+m+1;
					add(u,v,flow,cc);
				}
			}
			int tmp = min_cost_flow(sp,tp);
			sum+=tmp;
		}
		cout<<sum<<endl;
	}
	return 0;
}