最小生成树 - 普里姆算法java

最小生成树 - 普里姆算法java

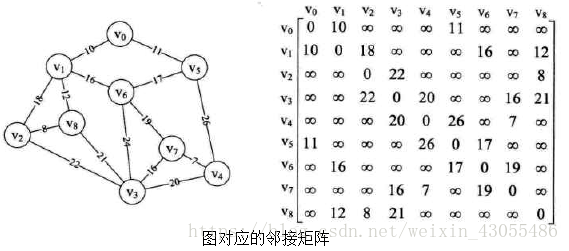把图用矩阵表示

---

【】先拿随机点作为起始点进行树的生长
【】把最小树已连接的点看做整体，从已被纳入树的点来寻找最近的可连接的点
【】筛选可以连接新的点的节点，找出它的最小的路径的点
【】如果最小长度等于无限长则说明已无法连接新的点，即全全部点已连接

  public class MinSpanTree {
    private int vertexSize; // 顶点个数
    private int[][] matrix; // 矩阵
    private boolean[] isVisited; // 标记被纳入到最小树的点
    private static final int MAX_WEIGHT = Integer.MAX_VALUE;
    private int[] minWeights; // 记录最小生成树的权值集合
    private int[] next; // 记录点可生成下一个没有纳入到树的最小权值的点
    private boolean[] ends; // 标记无法访问到新的点的点

    /**
     * 生成图
     */
    private void createGraph(int index) {
        vertexSize = index;
        matrix = new int[index][index];

        int[] a0 = { 0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT,
                MAX_WEIGHT, MAX_WEIGHT };
        int[] a1 = { 10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16,
                MAX_WEIGHT, 12 };
        int[] a2 = { MAX_WEIGHT, 18, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT,
                MAX_WEIGHT, 8 };
        int[] a3 = { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, 24, 16, 21 };
        int[] a4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT,
                7, MAX_WEIGHT };
        int[] a5 = { 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17,
                MAX_WEIGHT, MAX_WEIGHT };
        int[] a6 = { MAX_WEIGHT, 16, MAX_WEIGHT, 24, MAX_WEIGHT, 17, 0, 19,
                MAX_WEIGHT };
        int[] a7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19,
                0, MAX_WEIGHT };
        int[] a8 = { MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT,
                MAX_WEIGHT, 0 };

        matrix[0] = a0;
        matrix[1] = a1;
        matrix[2] = a2;
        matrix[3] = a3;
        matrix[4] = a4;
        matrix[5] = a5;
        matrix[6] = a6;
        matrix[7] = a7;
        matrix[8] = a8;
    }

    /**
     * 拿到已被添加到树的点下一个没有被添加到树的权值最小的点
     */
    public int getminWeight(int index) {
        int minWeight = MAX_WEIGHT;
        int nextIndex = 0;
        for (int i = 0; i < matrix[index].length; i++) {
            if (!isVisited[i] && matrix[index][i] != 0
                    && matrix[index][i] != MAX_WEIGHT) {
                if (matrix[index][i] < minWeight) {
                    minWeight = matrix[index][i];
                    nextIndex = i;
                }
            }
        }
        next[index] = nextIndex;
        if (minWeight == MAX_WEIGHT) {
            ends[index] = true;
        }
        return minWeight;
    }

    public int getMineTree() {
        ends = new boolean[vertexSize];
        minWeights = new int[vertexSize];
        next = new int[vertexSize];
        isVisited = new boolean[vertexSize];
        int sum = 0;
        int minWeight = 0;

        isVisited[0] = true; // 第一个点

        while (minWeight != MAX_WEIGHT) { // 判断点还能否产生新的分支
            int index = 0;
            minWeight = MAX_WEIGHT;
            for (int i = 0; i < isVisited.length; i++) {
                if (isVisited[i] && !ends[i]) { // 搜寻已在树内且还可产生新分支的点
                    if (getminWeight(i) < minWeight) {
                        minWeight = getminWeight(i);
                        index = i;
                    }
                }
            }
            if (minWeight != MAX_WEIGHT) {
                isVisited[next[index]] = true;
                minWeights[next[index]] = minWeight;
                sum += minWeight;
            }
        }
        return sum;
    }

    public static void main(String[] args) {
        MinSpanTree mst = new MinSpanTree();
        mst.createGraph(9);
        System.out.println(mst.getMineTree());
    }

}