2. 模型评估与选择
2.1 经验误差与拟合
1. 概念
- 模型:本书中指从数据中学得的结果
- 学习/训练(learning/ training): 通过执行某个学习算法从数据中学得模型
- 训练数据:学习/训练中使用的数据
- 训练样本:训练数据中的每个样本(sample)
- 训练集(set):训练样本组成的集合
2. 误差
- 训练/经验误差:学习器在在训练集上的误差
- 泛化误差:在新样本上的误差 (希望得到泛化误差小即在新样本上表现好的的学习器)
3. P和NP概念理解
-
多项式时间/P时间(Polynomial time):多项式时间在决定型机器上是最小的复杂度类别 ,算法复杂度通常表示为一个函数f(n),多项式时间中n必须为多项式,即 f ( n ) = n k f(n) = n^k f(n)=nk
-
P = “确定性计算机”能够在“多项式时间”解决的所有问题 。即一个问题可以在多项式时间里找到解决的算法
- 给出一段分支程序
if (x == 0) {
one();
} else {
two();
}
- NP = NP是指非确定性多项式(non-deterministic polynomial,缩写NP)。所谓的非确定性是指,可用一定数量的运算去解决多项式时间内可解决的问题。不太理解!!!
- “非确定性计算机”能够在“多项式时间”解决的所有问题。幻想出来一种机器,叫做“非确定性计算机”(nondeterministic computer),它可以同时运行这程序的两个分支,one() 和 two()。它的用处就在于,当你不知道 x 的大小的时候,根据 one() 和 two() 是否“运行成功”,你可以验证出 x 是否为零。即在多项式时间内验证一个解的问题。
-------------------------------NP问题例子-------------------------------------
-
例如,著名的推销员旅行问题(Travel Saleman Problem or TSP):假设一个推销员需要从香港出发,经过广州,北京,上海,…,等 n 个城市, 最后返回香港。 任意两个城市之间都有飞机直达,但票价不等。假设公司只给报销 C 元钱,问是否存在一个行程安排,使得他能遍历所有城市,而且总的路费小于 C?
推销员旅行问题显然是 NP 的。因为如果你任意给出一个行程安排,可以很容易算出旅行总开销。但是,要想知道一条总路费小于 C 的行程是否存在,在最坏情况下,必须检查所有可能的旅行安排! 这将是个天文数字。 -
旅行推销员问题是数图论中最著名的问题之一,即“已给一个n个点的完全图,每条边都有一个长度,求总长度最短的经过每个顶点正好一次的封闭回路”。
-
我的理解是np问题是要遍历所有可能情况,耗时很大。
=======================================================
4. P = NP?问题理解
-
“P=NP?”问题的目标,就是想要知道 P 和 NP 这两个集合是否相等。为了证明两个集合(A 和 B)相等,一般都要证明两个方向:
A 包含 B
B 包含 ANP 肯定包含了 P。因为任何一个非确定性机器,都能被当成一个确定性的机器来用。你只要不使用它的“超能力”,在每个分支点只探索一条路径就行。所以“P=NP?”问题的关键,就在于 P 是否也包含了 NP。也就是说,如果只使用确定性计算机,能否在多项式时间之内,解决所有非确定性计算机能在多项式时间内解决的问题。
5. 过拟合/欠拟合 (overfitting/underfitting)
- 过拟合概念:学习器将训练样本学得太好了,将训练样本自身的一些特点当做了所有潜在样本都会具有的一般性质,使泛化(特殊到一般归纳)性能下降,即学到了训练样本不太一般的特性
-
过拟合无法避免,只能缓解,是机器学习的关键障碍,各类算法都有针对过拟合的措施
-
机器学期面临的问题通常为NP难问题或更难,有效的学习算法必然是在多项式时间内运行完成,;只要相信P≠NP,过拟合就不可避免。
-
反证法:
过拟合为np问题
假设过拟合问题可在多项式时间内解,则过拟合为p问题
前提条件是相信P≠NP,则过拟合不不可解
我的理解是只要相信不是所有的np问题,即所有需要遍历所有情况的问题,(例如过拟合中会将训练样本的的特性都学完??)都可以在多项式时间内解决(变成p问题)即找不到最优解?(NFL?绪论中最后提到每种问题出现的概率其实是一样的,所以需要归纳偏好,针对具体问题确定偏好,选择算法,这个算法未必是最优解???)过拟合就不可避免。
2.2. 评估方法
2.2.1. 概念
- 预测:对训练集学习,建立从输入空间(样本空间)到输出空间(样例空间,即结果)的映射
- 测试testing:学得模型后,使用模型进行预测
- 测试样本:被预测的样本(新样本)
- 独立同分布:假设样本空间中全体样本服从一个未知的分布D, 我们获得的每个样本都是独立地从D上采样获得,即iid
2.2.2. 模型选择(model selection)问题
- 定义:对于一个学习算法,使用不同参数配置,会产生不同模型,选用哪一种参数配置的问题就是模型选择问题
- 理想解决方案:评估候选模型的泛化误差(在新样本上的误差),选泛化误差最小的模型。
- 但泛化误差无法直接获得,即新样本无法直接获得
- 训练误差有过拟合现象不适合作为标准
- 因此现实中我们通过实验测试评估学习器的泛化误差,进而选择一种参数配置即模型选择
2.2.3. 评估方法
- 上文提到通过实验测试评估泛化误差来选择模型。
- 实验测试需使用一个测试集:测试学习器对新样本的判别能力
再以测试集上的测试误差近似泛化误差
-
测试样本:假设从样本真实分布中独立同分布采样而得
-注意:测试集尽量与训练集互斥。即测实样本尽量不在训练集中出现。否则结果过会过于乐观 -
但只有一个包含样例的数据集D,我们对D进行适当处理,从中产生训练集S和测试集T。
方法如下:
- 留出法(hold-out)
将数据集D划分为两个互斥集合:训练集S,测试集T。在S训练出模型后用T评估其测试误差
- S/T的划分要尽可能保持数据分布的一致性。用分层采样
- 缺点:单次使用留出法结果不稳定可靠:不同的划分导致不同的S/T。相应的模型评估也有差别。S小则结果偏差较大;T小则方差较大
- S和T的划分比例还没有完美解决方案,常见做法S占2/3~4/5
- 交叉验证法
将D划分为k个大小相似的互斥子集,每次用k-1个子集的并集作为S,剩下的作为T。
- 分层采样,保持一致性
- 最终返回k次测试结果的均值

-
因存在多种划分方式,k折交叉验证通常要随机使用不同的划分重复p次
-
最终评估结果是这p次k折交叉验证结果的均值
-
留一法:LOO,每个子集含一个样本
- 优点:准确:使用的S与D相比只少了一个样本
- 缺点:数据集较大时,训练量太大
- 自助法(bootstrapping)
- 留出法、交叉验证法缺点:保留了一部分样本用于测试,实际评估的模型用的S比D小,受训练样本规模变化影响;留一法受影响较小,但计算复杂度太高
自助法:D包含m个样本,每次从D中有放回地挑选一个样本放入D1,重复执行m次,得到包含m个样本数据集D1。
- 样本在m次采样中始终不被采样到的概率是 ( 1 − m ) m (1-m)^m (1−m)m,极限为0.368。
- 优点:
- 将D1用作S, D-D1用作T,仍有数据总量1/3,没在D1中出现的样本用于测试,
- 实际和期望评估的模型都使用m个训练样本
- 适用于数据集较小时。数据量足够时,用留出法和交叉验证法
- 缺点:
- 会引入估计偏差
,
- 会引入估计偏差
2.2.4. 调参与最终模型
- 调参(parameter tuning):模型评估与选择时,除了选择学习算法,还需对算法进行参数设定,参数配置不同,学得模型也有显著差别。
- 调参工程量往往很大,如深度学习
- 验证集(validation set):模型评估与选择中用于评估测试的数据集
- 训练数据分为:
- 训练集: S
- 验证集:T
- 测试数据:在实际使用中遇到的数据
在研究对比不同算法的泛化性能时用:
- 测试集上的泛化效果:估计模型实际使用时的泛化能力
- 验证集上的性能:进行模型选择和调参
为什么要划分?:防止过度拟合
总结:

- training set是用来训练模型或确定模型参数的,如ANN中权值等;
- validation set是用来做模型选择(model selection),即做模型的最终优化及确定的,如ANN的结构;
- test set则纯粹是为了测试已经训练好的模型的推广能力。当然,test set这并不能保证模型的正确性,他只是说相似的数据用此模型会得出相似的结果。
- 但实际应用中,一般只将数据集分成两类,即training set 和test set,大多数文章并不涉及validation set。
2.3. 性能度量(performance measure):本节主要研究分类任务(离散)
- 性能度量:衡量模型泛化能力的评价标准,反映了任务需求(上一节讲的都是实验估计方法)
- 给定样例集D{(X1,Y1),(X2,Y2)…,(Xm,Ym)}
要评估学习器f的性能,就要把预测结果f(x)和真实标记y进行比较 - *均方误差(mean squard error):回归(连续)任务常用


2.3.1错误率与精度
- 分类任务中常用性能度量
- 错误率(error rate):分类错误的样本数占样本总数的比例。E=a/m
- 精度(accuracy):1-E
- 对样例集D的分类错误率:
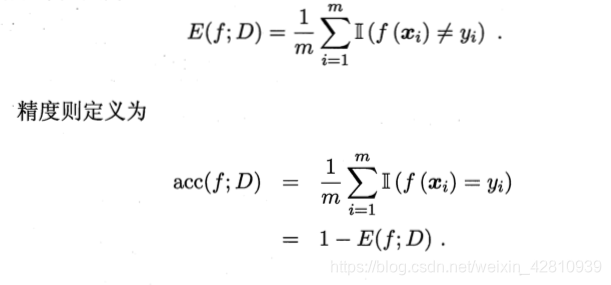

2.3.2. 查准率、查全率、F1
错误率和精度不能满足所有任务需求。信息检索、web搜索中常出现:检索出的信息有多少比例是用户感兴趣的。等需求,查准率查全率更适合此类需求的性能度量
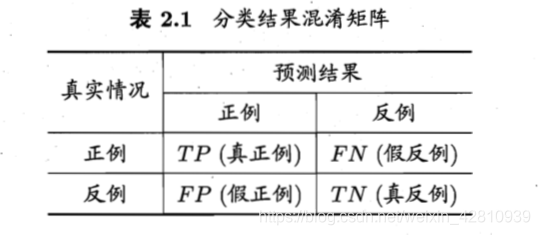
1. 将样例划分为四种情形(根据样例的真实类别y和学习器预测类别f**)
- True/False表示学习器预测结果的正确与否
- Positives/Negatives:表示学习器预测结果
TP(true positive):真正例(被模型预测为正的正样本)
FP(false positive):假正例(被模型预测为正的负样本)
TN(true negative):真反例
FN(false negative):假反例
- TP + FP + TN + FN = 样例总数
TPR真正例率:查全率
FPR假正例率:分母为真实类别为负样本总数

2. 查准率P = T P T P + F P \frac{TP} {TP + FP} TP+FPTP
- P(Precision, 精度): 是针对预测结果而言的,它表示的是预测为正的样本中有多少是真正的正样本。
3. 查全率R = T P T P + F N \frac{TP} {TP + FN} TP+FNTP
- R召回率(Recall, 又称为 TPR): 是针对原来的样本而言的,它表示的是预测结果与真实类别相一致的(即被预测正确的结果)的样本中有多少被预测为正的正样本。
4. P 、R关系
-
二者矛盾
-
P-R图

- 性能优着曲线完全包住性能低者(面积越大,性能越好)
- 平衡点BEP:综合考虑查准率查全率,是P = R时的取值
- F1度量
-

-
F1度量的一般形式:Fβ

-
- 有多个二分类混淆矩阵时要在各混淆矩阵上分别计算出P、R记为(P1,R1)…(
P
n
,
R
n
)
P_n,R_n)
Pn,Rn)
- 宏查准率macro-P
- 宏查全率macro-R
- 宏F1
- 也可先将各混淆矩阵的对应元素平均,得到TP FP TN FN 的平均值,基于平均值算出
- 微查准率micro-P
- 微查全率
- 微F1
2.3.3 ROC、AUC
1. 分类学习器的预测类别
- 测实样本产生一个实值或概率预测,将之与一个分类阈值threshold进行比较分类(即上节提到的学习器预测类别)
- 正类(正例):大于阈值
- 反类(反例):小于阈值
很多情形下, 我们可以根据学习器的预测结果对样例排序, 排在前面的是学习器认为"最可能"的正例的样本, 排在后面的是学习器认为"最不可能"是正例的样本. 以某个截断点(cut point)将样本分为两部分,前一部分为正例,后一部分为反例
- 更重视P:则在排序靠前位置截断
- 更重视R:在排序靠后位置进行截断
2. ROC
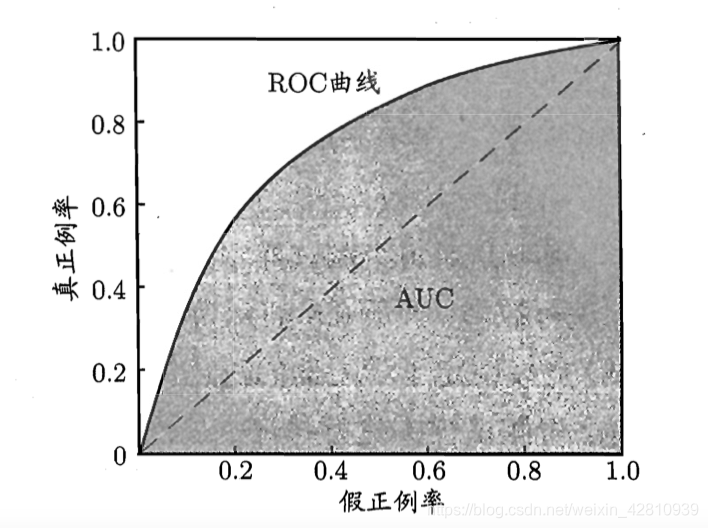
- 1)定义:ROC.(receiver operating characteristic), 其显示的是分类器的真正率TPR和假正率TFR之间的关系
3. AUC
1)AUC(area under ROC curve), 即 ROC 曲线下方的面积
考虑的是样本预测的排序质量
在正负失衡的情况下,从ROC曲线看分类器的表现仍然较好(图c),然而从P-R曲线来看,分类器就表现的很差, 也就是说样本不均衡时, 使用 P-R 曲线更能区分不同分类器的性能.
2.3.4 代价敏感错误率与代价曲线
前面介绍的一些性能度量,都假设了均等代价
1. 为权衡不同类型错误造成的不同损失,为错误赋予非均等代价(unequal cost)
-
在非均等代价下,更希望最小化总体代价而不是错误次数
-
非均等代价下,**代价曲线(cost curve)**可以反映出学习器的期望总体代价,ROC不可以

-
ROC曲线上每个点转化为代价平面上一条线段,所有线段下界围成的面积为在所有条件下学习器的期望总体代价
2.4 比较检验
机器学习中性能比较很复杂,不单单通过实验评估就可以
统计假设检验(hypothesis test)为比较性能提供重要依据
2.4.1 假设检验
此假设是对学习器泛化错误率分布的猜想,只能知道测试错误率,可由此推出泛化错误率
1. 对单个学习器的泛化性能假设检验
- 二项分布
一次留出法估计 - t检验
多次重复留出法或交叉验证法得到多个测试错误率
2. 对多个不同学习器如下
- 在一个数据集上比较两个算法的性能
- 交叉验证t检验
- 对两个学习器
- McNemar检验
- 对二分类问题
- 在一个数据集上对多个算法比较
- 基于算法排序的Friedman检验
- Nemenyi 后续检验(post-hoc test)
2.5 偏差与方差
了解学习算法为什么具有这样的性能:偏差-方差分解(bias-variance decomposition)工具
- 方差(使用样本数相同的不同训练集):
- 刻画数据扰动造成的影响

- 刻画数据扰动造成的影响
- 噪声:刻画学习问题本身的难度

- 偏差(期望输出与真实标记的差别)bias
- 刻画学习算法的拟合能力

- 刻画学习算法的拟合能力
泛化误差为偏差方差与噪声之和

-
偏差方差冲突
-
三者关系图

3.线性模型
3.1 基本形式
3.1.1.概念
- 示例/样本(instance/sample)/特征向量:数据集中的每条记录
- 属性空间/样本空间/输入空间:属性张成的空间,例如色泽、根蒂、敲声作为三个坐标轴,张成用于描述西瓜的三维空间。
- 特征向量(feature vector):样本空间中每个点对应一个坐标向量。因此一个示例也称为一个“特征向量”
- 矢量和矩阵

行向量的元素是用空格或逗号隔开,列向量则用分号隔开。
3.1.2. 线性模型(linear model):用于预测结果f(x)
A. 线性:量和量之间按比例、成直线的关系,一阶导数为常数,空间和时间上代表规则和光滑的运动
B. 非线性non-linear:则指不按比例、不成直线的关系,代表不规则的运动和突变,一阶导数不为常数。
- 给定由d个属性描述的示例x = (x1,x2,… x d x_d xd)
-
定义:线性模型试图学得一个通过属性的线性组合来进行预测的函数

-
向量形式: f ( x ) = w T x + b f(x) = w^Tx + b f(x)=wTx+b
其中w = (w1,w2,…, w d w_d wd),可以认为是各属性的权重,x = (x1; x2;…;xd),都是矩阵)
- w T w^T wT为w矩阵的转置
- wi的大小直观表达了各属性在预测中的重要性
3.2 线性回归
3.2.1. 概念
- 输出标记
- arg 是变元(即自变量argument)的英文缩写。
arg min 就是使后面这个式子达到最小值时的变量的取值
arg max 就是使后面这个式子达到最大值时的变量的取值 - 均方误差:
- 欧几里得距离:m维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离)。在二维和三维空间中的欧氏距离就是两点之间的实际距离。
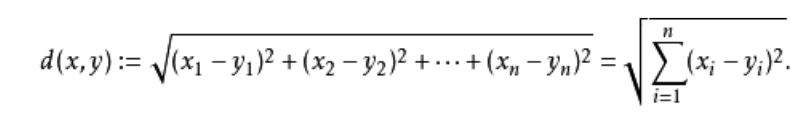
3.2.2. 线性回归(linear regression)
本节讨论如何用线性模型进行回归学习
- 给定数据集(示例集)D = {(X1,Y1),…,(Xm,Ym)}
1. 定义:线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记
2. 输入属性数目只有一个时
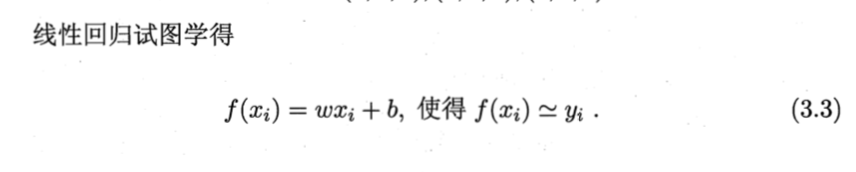
-
离散属性值之间存在序order关系时,连续化将其转化为连续值,例如:
- 二值属性“身高”:“高”和“矮”可以转化为{1.0, 0.0}
- 三值属性“高度”:
-
不存在序关系,若有k个属性值,则转化为k维向量
- “瓜类”:例如属性"瓜类"的取值"西瓜" “南瓜” "黄瓜"可转化为(0 , 0 , 1) , (0, 1 ,0), (1 ,0, 0)。
-
对于连续型数据,我们也可以通过一些方法将其离散化。离散化有很多的好处,比如能够使我们的模型更加的简单,因为相对于连续类型数据,离散类型数据的可能性更少。对于某些模型比如计算广告中常用的逻辑回归,是非常需要我们输入离散化的特征的。
3. 线性模型中如何确定w和b:均方误差最小化(最小二乘法)
即:f(xi)表示学习器模型的预测输出,yi是真实值

均方误差有非常好的几何意义,它对应于**“欧氏距离”**。(见概念)
-
最小二乘法:使均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归中,最小二乘法就是找到一条直线,使所有样本到直线的欧氏距离之和最小。
-
线性回归模型的最小二乘“参数估计”:求解w,b使均方误差E(w,b) = Σ 1 m ( y i − w x i − b ) Σ^m_1(y_i-wx_i-b) Σ1m(yi−wxi−b)最小化的过程(重点在求解参数w和b)
要求均方误差E的最小值,可以用求极值的方法,即:
将均方误差E对w和b分别求偏导并令其为0,求出w,b
计算过程如下:
4. 多元线性回归(更一般的情况,数据集D,样本由d个属性描述)
此时试图学得:
参数估计w,b:最小二乘法
求解过程见下图:

求导过程:

参考: https://www.jianshu.com/p/e2c20f0c3f7e
5. 对数线性回归(逼近y的衍生物)
当线性模型预测值f(x)逼近真实标记y时,就得到了线性回归模型,即之前讨论的
也可以令模型预测值逼近y的衍生物,我们为便于观察将线性回归模型简写为y = ωTx + b 。例如假设我们的样本所对应的输出标记是在指数尺度上变化,可用输出标记的y = g-1(ωTx + b)作为线性模型逼近的目标:lny = ωTx + b ,这就是对数线性回归
- lny = ωTx + b 形式上是线性回归,但实际上是让e^(ωTx + b)逼近y,是求输入空间到输出空间的ωTx + b函数映射

6. 广义线性模型(generalized linear model)
对数函数起到了将线性回归模型的预测值f和真实标记y联系起来的作用
更一般地,单调可微函数g(.),令
- 这个模型叫广义线性模型(3.15)
- 单调可微函数g(.)为联系函数(link function)
- 对数线性回归是广义线性模型在g(.) = ln(.)时特例(?)
3.3 对数几率回归(Logistic Regression)(逼近y的对数几率函数ln y 1 − y \frac{y}{1-y} 1−yy )
通常写成
就得到我们熟悉的Logistic Regression的形式
- 其实就相当于线性模型的输出加了一个激活函数,这个激活函数就是大名鼎鼎的sigmoid函数,其实也叫做logistic function,所以Logistic Regression中的Logistic是出自 Logistic function,而Logistic function 就是我们常说的sigmoid函数。此函数可以把x映射到(0,1),恰恰符合我们的概率取值。
https://blog.youkuaiyun.com/u011995719/article/details/77529962
3.3.1 单位阶跃函数(unit-step function)
上一节讨论用线性模型进行回归学习
要做的是分类任务时:
- 分类任务:找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值f(x)联系起来
二分类任务:输出标记y∈{0,1},线性回归模型产生的预测值z是实值,需要将实值z转换为0/1,可用单位阶跃函数实现


- 单位阶跃函数不连续,所以不可微,连续函数要单调可微,所以单位阶跃函数不能直接用作
g
−
g^-
g−(.)。
因此我们想找到近似单位阶跃函数的,单调可微的替代函数----------对数几率函数
3.3.2 对数几率函数(logistic function)(对率函数)
- 和对数函数ln不同
- 近似单位阶跃函数的替代函数
- 单调可微
对数几率函数:y =
1
1
+
e
−
z
\frac{1}{1+e^-z}
1+e−z1 是一种“Sigmoid”函数

- 将对率函数用作
g
−
g^-
g−带入3.15广义线性模型y =
g
−
1
g^-1
g−1(ωTx + b)
得到(即令z = ωTx + b )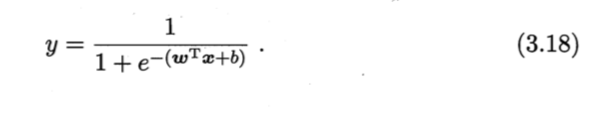
分式化整式再取对数得到: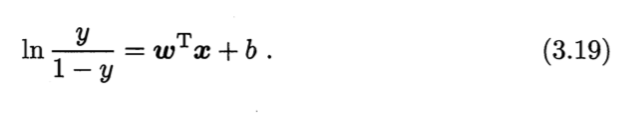
计算过程如下图:
- 几率(odds):
y
1
−
y
\frac{y}{1-y}
1−yy
y为样本x为正例的可能性,1-y为x作为反例的可能性 - 对数几率(logit/ log odds):ln y 1 − y \frac{y}{1-y} 1−yy
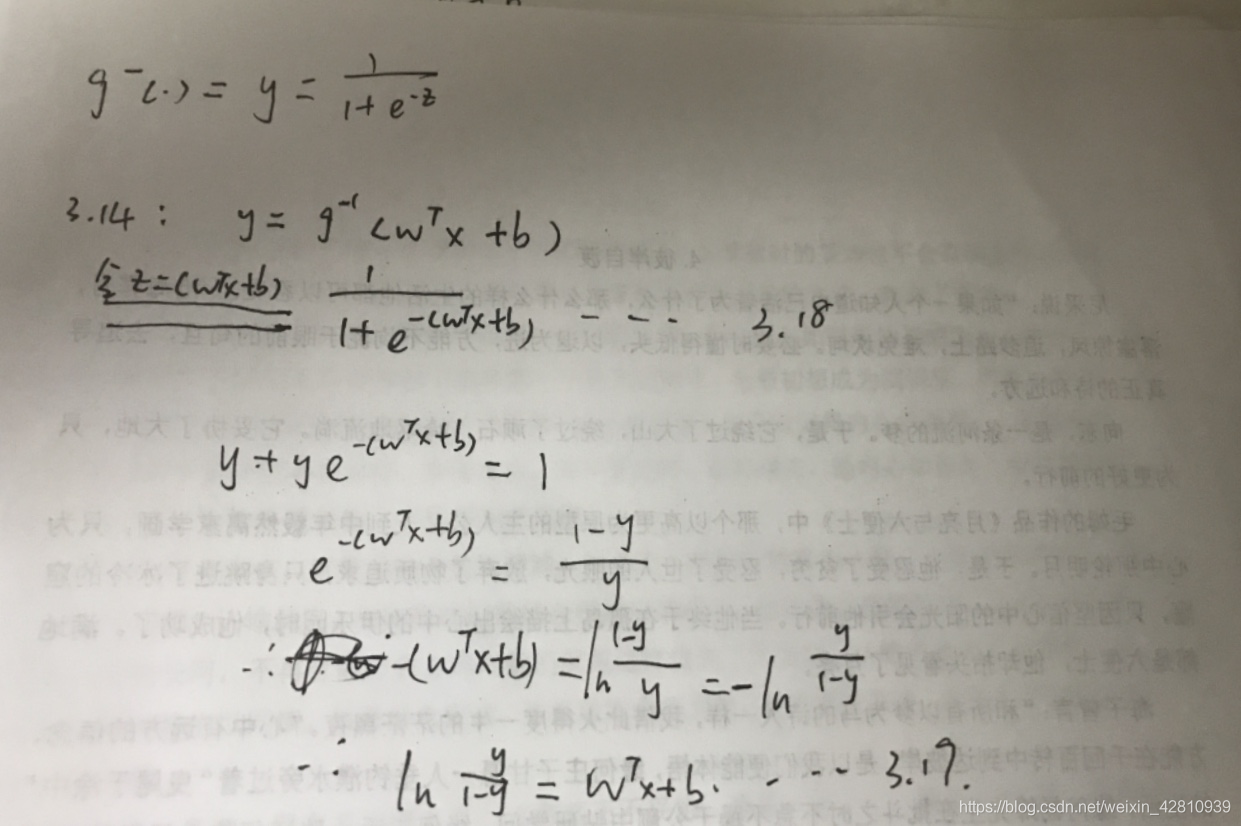
所以3.18是在用线性回归模型的预测结果z= ωTx + b 去逼近真实标记y的对数几率(式3.19)
3.3.3 对应得到的模型称为“对数几率回归”
- 不仅预测类别,还得到近似概率预测
- 是任意阶可导的凸函数
3.3.4 确定式3.18中的w和b(极大似然法)

名字虽然叫回归,但是是一种分类学习方法
可通过极大似然法(maximum likelihood method)估计w和b的值,(目前还未仔细研究)

总结起来,最大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
- 原理:极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
即另每个样本属于其真实标记的概率越大越好
参考:https://blog.youkuaiyun.com/qq_39355550/article/details/81809467

3.25中似然项可重写为:

3.26带入3.25

后面的求解可通过梯度下降法gradient descent method、牛顿法Newton method求解。


3.4 线性判别分析LDA
一种经典的线性学习方法
3.4.1 线性判别分析(LDA)
1. LDA思想
给定训练样例集,将样例投影到一条直线上,使同类样例的投影点尽可能接近、异类尽可能远离。
对新样本分类时,将样本投影到这条直线,根据投影点位置确定新样本类别
2. LDA二维示意图(二分类问题)

LDA是找一个投影,这个投影:
同类距离要小,异类距离要大,这个距离用协方差矩阵衡量:
- 要使同类样例投影点尽可能接近:让两个同类样例投影点的协方差尽可能小:
投影后的类内距离用 wTΣ0w来衡量,其中 Σ0是第0类的协方差矩阵(在此仅考虑二分类问题)。 w T Σ 0 w + w T Σ 1 w w^TΣ_0w+w^TΣ_1w wTΣ0w+wTΣ1w 尽可能小 - 要使异类样例投影点尽可能远离:
可以采用类别中心之差来衡量,即∥∥wTμ0−wTμ1∥∥2
,其中μ0,μ1分别是第0类和第1类的均值向量。让两类样本的中心之间的距离尽可能大: ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 ||w^Tμ_0-w^Tμ_1||^2_2 ∣∣wTμ0−wTμ1∣∣22 尽可能大 - 同时考虑1、2,让协方差作为分子尽可能小,中心间距离作为分母尽可能大,可得到最大化目标J


 ###### 定义:
###### 定义:
- 类内散度矩阵:
S
w
S_w
Sw

- 类间散度矩阵:
S
b
S_b
Sb

重写J:得到广义瑞利商(这就是LDA欲最大化的目标)

https://www.jianshu.com/p/be4017dd42bd
确定w(还没仔细研究)
- 一些概念
- 拉格朗日乘子法(类似高数的条件极值的求法)
- 奇异值分解
- 实对角矩阵
https://blog.youkuaiyun.com/Banach_I/article/details/51078451 - 贝叶斯决策理论
LDA被视为一种经典的监督降维技术
3.4.3 LDA推广到多分类任务中
- 概念
- 矩阵的迹(trace):矩阵对角线上元素之和
-
全局散度矩阵:类内Sw+类间Sb


-
多分类LDA有多种实现方法,常见采用优化目标

3.5 多分类学习
- 基于一些几本策略,利用二分类学习器来解决多分类问题:如LDA推广
- 本节主要介绍如何对多个分类器进行拆分
3.5.1. 多分类学习的基本思路:拆解法
- 即将多分类任务拆为若干个二分类任务求解
- 对问题拆分成若干个二分类任务
- 为每个二分类任务训练一个分类器
- 测试时:对分类器们的预测结果进行集成,获得最终的多分类结果
3.5.2.拆分策略
- OVO
- OVR
- MVM

1. ovo
给定含有m个样例的数据集D, y i ∈ C 1 , C 2 , . . . . . . . . C N y_i∈{C_1,C_2,........C_N} yi∈C1,C2,........CN
- 将N个类别两两配对,产生N(N-1)/2个分类任务
- 被预测的最多的类别作为最终分类结果
2. ovr
- 预测置信度
每次将一个类的样例作为正例,所有其他类作为反例训练N个分类器 - 测试时若只有一个分类器预测为正类,则对应类别标记作为最终分类结果
- 多个预测正类,则预测置信度最大的分类器的类别标记作为分类结果
3. ovo和ovr区别
- ovo存储开销和测试时间开销通常比ovr更大
- 但在类别很多时,因为ovo每个分类器只用到两个类的样例,ovr要使用全部训练样例,所以ovo训练时间开销更小。
4. MvM
- 每次将若干个类作为正类,若干个其他类作为反类。
- ovo、ovr是mvm的特例
5. ECOC编码(纠错输出码(error correcting output codes))
1). ECOC能将多类问题两类化:对输出类别进行编码
即每个类别对应一个长度为m的二进制串(m个分类器),共形成n(类别数)个二进制串。(见编码矩阵)
- MvM的正反类构造要有特殊的设计,用到MvM技术:
- ECOC将编码的思想引入类别拆分,并尽可能在解码的过程中具有容错性。
2)编码矩阵(coding matrix)
二元码:正反类
三元码:停用类
1、编码:对n个类别做m次划分,产生m个训练集,训练出m个分类器
- 如图,4个类别做5次划分,训练出5个分类器f
2、解码:M个分类器分别对测实样本进行预测,预测标记Yi组成一个编码,返回其与自身编码距离最小的类别作为最终预测结果
- 如图,5个分类器f的预测结果连个起来形成了测试示例的编码:-1-1+1-1+1
- C1自身编码:-1+1-1+1+1
- C1类对应的自身编码和预测结果的测试示例编码比较,求距离,距离最小的编码作为预测结果。
- 例如C1和测试示例编码欧式距离2 3 \sqrt{3} 3,而最小距离是C3的2,所以预测结果是C3

3、ECOC纠错功能:
- 在测试阶段,假如某个分类器出错了,例如f2出错导致C3的错误编码(-1,-1,+1,-1,+1),仍能产生正确的最终分类结果C3.
- ECOC编码越长,需要训练的分类器越多,纠错能力越强,存储计算开销增大
- ECOC编码能起到理想纠错作用的重要条件是:在每一位编码上出错的概率相当且独立。
3.6 类别不平衡问题
3.6.1 类别不平衡(class-imbalance)
指分类任务中不同类别的训练样例数目差别很大。本节假设正例样例较少
1. 线性分类器角度
预测几率
y
/
(
1
−
y
)
y/(1-y)
y/(1−y) 反映了正例可能性和反例可能性比值
观测几率
m
+
/
m
−
m^+/m^-
m+/m−,代表真实几率
- 只要预测几率高于观测(真实)几率则判定为正例

但分类器基于预测几率进行决策,所以要对预测值进行调整,使决策时,实际是在执行3.47.做到这一点可用:
2. 类别不平衡学习的基本策略:再缩放(rescaling)/再平衡
令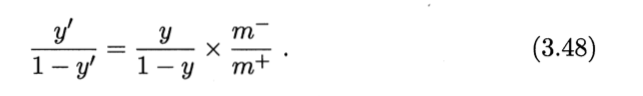
再缩放实际操作不平凡,因为训练集是真实样本总体的无偏采样往往不成立。解决这个问题可采用:
- 欠采样:去除一些反例(时间开销小于过采样)
- EasyEnsemble算法,将反例化分为若干个集合供不同学习器使用,每个学习器都进行了欠采样,但全局不会丢失信息
- 过采样:增加一些正例(不能对初始正例样本进行重复采样,会导致过拟合)
- SMOTE算法,对正例插值
- 阈值移动:在用训练好的分类器预测时,将3.48嵌入到决策过程中
5. 神经网络(neural networks)
5.1 神经元(neuron)模型
5.1.1 概念
- 神经网络:神经网络是由具有适应性的简单单元(神经元模型)组成的广泛并行互连的网络,他的组织能够模拟生物神经系统对真实世界物体作出的交互反应。(机器学习中讨论神经网络学习)
- 神经元模型:神经网络中最基本的成分
5.1.2 神经元模型
1. M-P神经元模型


- 神经元接受n个其他神经元传来的输入信号
- 输入信号通过
∑
1
i
w
i
⋅
x
i
∑^i_1w_i⋅x_i
∑1iwi⋅xi+b
的连接进行传递:总输入值z = ∑ 1 i ∗ w i ⋅ x i − θ ∑_1^i*w_i⋅x_i-θ ∑1i∗wi⋅xi−θ = w T x + b w^Tx + b wTx+b - 总输入值和阈值比较
- 通过激活函数f(z)处理输出,得到加权值通过激活函数f/σ非线性化的最终输出结果(现实生活中,很多分类是非线性的,通过激活函数非线性化)

2. 激活函数
- 引入激活函数的原因:如果不用激活函数(相当于f(x)=x),每一层输出都是上一层输入的线性组合,与只有一个隐藏层效果相当。
①理想激活函数:阶跃函数(0、1)
理想的激活函数是a所示的阶跃函数,它将输入值映射为输出值“0”或“1”,显然“1”对应于神经元兴奋,“0”对应于神经元抑制。 然而阶跃函数具有不连续、不光滑等不太好的性质,因此实际常用Sigmoid函数作为激活函数,它将可能在较大范围内变化的输入值挤压到(0,1)输出值范围内。
②sigmoid型函数(挤压函数squashing function)
sigmoid型函数是一类S型曲线函数,对数几率回归中也用到,作为单位阶跃函数的替代函数
- 常用sigmoid函数:

tanh函数可以看做是放大并平移的logistic函数:


3. 神经网络(多个神经元按一定的层次结构连接)
一个神经网络:包含了许多参数的数学模型,模型是若干个函数(例如 y j y_j yj = = ∑ i ∗ w i ⋅ x i − θ j ∑_i*w_i⋅x_i-θ_j ∑i∗wi⋅xi−θj)相互嵌套带入而得,即把许多神经元按一定层次结构连接起来
5.2 感知机与多层网络
5.2.1 感知机(perceptron)
1. 感知机:由两层神经元组成,

2. 感知机实现与或非运算,假定f为阶跃函数,激活函数y = f(Σi wi*xi - θ)

- 与运算:分配权重令w1 = w2 = 1 ; 设置阈值θ = 2 ,则y = f(x1+x2-2)
- Xn ∈{0,1}, 所以X1+X2 = 2或1或0 ,只有二者同时为1时,阶跃函数y(0)才能取值为1,做到逻辑与运算
- 或运算:分配权重令w1 = w2 = 1 ; 设置阈值θ = 0.5 ,则y = f(x1+x2-0.5)
- 只有当x1,x2同时为0,y(-0.5)=0,其他情况x1,x2只要有一个为1,y值为1
- 非运算:分配权重令w1 =-0.6, w2 = 0 ; 设置阈值θ = -0.5 ,则y = f(-0.6*x1 + 0.5)
- x1 = 1时,y(-0.1)= 0
- x1 = 0时, y(0.5)= 1 实现非运算
3. 更一般情况,给定训练数据集,w和θ可以通过学习得到
1、权重和阈值统一为权重的学习:将θ看作一个哑结点(固定输入为-0.1)所对应的连接权重Wn+1.则权重w和阈值θ的学习就可统一为权重的学习
2、感知机的学习规则
训练样例(x,y),若当前感知机输出为y^
学习率:η
调整感知机权重:
若感知机预测正确则y = y^, △wi = 0,权重wi不变
3、 感知机学习能力有限,只拥有一层功能神经元(只有输出层神经元进行激活函数处理)
一层功能神经元,解决线性可分问题
4、与或非问题都是线性可分问题,
若两类模式线性可分,存在一个线性超平面能将这两类分开,感知及学习过程一定收敛,可以求到合适的权重向量w(w1;w2…;wn+1),wn+1为阈值θ
5、异或为非线性可分问题,感知机学习过程会发生震荡(fluctuation),不能求到合适的w

6、 解决非线性可分问题,如异或问题,使用多层功能神经元
- 隐含层:输入输出层之间的神经元(有激活函数功能)
没有隐含层的神经网络是线性的,只能处理线性可分的问题,就相当于线性的Logistic模型。 - 两层感知机解决异或问题,(感知机由两层神经元组成)

7、更一般的常见神经网络:多层前馈神经网络

输入层:接受外界输入,不进行函数处理
隐层和输出层神经元:对信号进行加工
4. 神经网络的学习过程:
根据训练数据调整:
- 神经元间“连接权”(connection weight)
- 每个功能神经元的阈值
神经网络学到的东西蕴含在连接权与阈值中
5.3 误差逆传播算法(反向传播算法)
欲训练多层网络,需要更强大算法:
5.3.1 误差逆传播算法(BP算法)
- 可用于多层前馈神经网络和其他类型如:训练递归神经网络
通常说BP网络时:一般指BP算法训练的多层前馈神经网络

-
假设隐层和输出层神经元都使用sigmoid函数
假定神经网络输出 = f(βj - θj)
网络在训练样例上的均方误差 -
确定参数(权重w和阈值θ的学习就可统一为权重的学习,即求权重值)
输入层d到隐层q的权值:dq
隐层q到输出层l:ql
隐藏神经元阈值:q
输出层神经元阈值:l
共有dq +ql +q +l = (d+l+1)q + l 个参数需要确定 -
参数更新估计
和5.1类似

任意参数v(也是权重值)更新估计式:v+△v → v
2. 推导(以隐层到输出层的连接权Whj为例)
- 思路
要对参数Whj进行更新,则要求出5.6中的均方误差对Whj的偏导
(这是 BP算法基于梯度下降策略,以目标的负梯度方向对参数进行调整)
要求这个偏导,就要把他链式法则展开有三个偏导要求解

则我们需要求出几个式子:(见图片)


- 均方误差公式Ek
- 输出值y公式
- 第j个输出神经元yj的输入总值βj
- 第一个和第三个偏导直接求出
- 中间的偏导用sigmoid函数的性质求
- 这三个偏导全都用 y j k y^k_j yjk(带上角标)表示,则均方误差和输出神经元的梯度都可以求出,同理阈值θj和γh也可以求出
求出了更新的隐层和输出层之间的连接权Whj,我们也可以把输入层和隐层的连接权Vhj求出来,和上面步骤相同,为了使求解过程清晰,我们最好把Ek再次展开,这次展开有两层,具体推导过程见下图:


https://blog.youkuaiyun.com/aaalswaaa1/article/details/84453155
- 标准BP算法的工作流程

- BP算法的目标:最小化训练集D上的累积误差:

3.累积BP算法
- 上面讨论的是针对一个训练样例更新连接权和阈值,是基于单个Ek推导的,叫标准BP算法。参数更新比较频繁,需要多次迭代
- 若类似标准BP算法推导出基于累积误差最小化的更新规则,就得到累积误差逆传播算法,即累积BP算法。累积BP直接针对累积误差最小化,读取整个训练集D一遍后才对参数进行更新,更新频率低。
- 训练集D非常大时,标准B往往会更快获得较好的解
- BP网络过拟合
由于其强大的表达能力,其训练误差持续降低,测试误差却可能上升,造成过拟合。
有两种策略缓解过拟合:
-
早停(early stopping)
将训练数据分为:训练集、验证集- 训练集:计算梯度、更新连接权和阈值
- 验证集:估计误差
若训练集误差降低、验证集误差升高则停止训练、返回具有最小验证集误差的连接权和阈值。
-
正则化(regularization)
基本思想:在误差目标函数中增加一个用于描述网络复杂度的部分,如:连接权和阈值的平方和。(训练过程会偏向比较小的连接权和阈值,使网络输出更光滑,对过拟合缓解)
令Ek表示第k个训练样例上的误差,则5.16

变为(wi表示连接权和阈值)
5.4 全局最小与局部极小
5.4.1 参数寻优(找全局最小)
神经网络的训练过程可看做参数寻优过程,即在参数空间中找一组最优参数使E(关于w和θ的函数)最小。
两种最优:
局部极小、全局最小

参数空间梯度为零的点(变化率为零),只要其误差函数值小于邻点的误差函数值,就是局部极小点。如图,有两个局部极小,一个全局最小。

基于梯度的搜索是最广泛的参数寻优方法:例如梯度下降法是沿着负梯度方向搜索最优解。若Ek在当前点的梯度为0则达到局部极小,参数的迭代更新在此停止。
- 若Ek只有一个局部极小则,则这个局部极小就是全局最小
- 若Ek有多个局部极小,则称参数寻优陷入了局部极小,为了跳出局部极小,进一步接近全剧最小,采用以下策略:
1、 多组不同参数值训练,取其中误差最小的解作为最终参数
2、用模拟退火(simulated)技术:在每一步都以一定概率接受比当前解更差的结果。可能也会造成跳出全局最小
3、使用随机梯度下降,计算梯度时加入了随机因素,即使达到了局部最小点,算出的梯度仍可能不为零,就可跳出
4、也常用遗传算法(genetic algorithms)
5.5 其他常见神经网络
5.5.1 RBF(radial basis function 径向基函数)网络
是一种单隐层前馈神经网络,隐层神经元的激活函数是径向基函数,输出值是对隐层神经元输出的线性组合。
假定输入为d维向量x,输出实值,RBF网络表示为:


两步训练RBF网络:
- 确定神经元中心ci
- BP算法确定参数wi和βi
5.5.2 ART(Adaptive Resonance Theory 自适应谐振理论)网络
-
ART是竞争学习的重要代表
竞争学习:神经网络中常用无监督学习策略,络的输出神经元相互竞争,每一时刻仅有一个竞争获胜的神经元被激活。胜者通吃原则 -
ART比较好地缓解了竞争型学习中的**“可塑性-稳定性窘境”(stability-plasticity dilemma**),可塑性是指神经网络要有学习新知识的能力,而稳定性则是指神经网络在学习新知识时要保持对旧知识的记忆。
-
ART具有一个很重要的优点:可进行增量学习incremental learning或在线学习online learning。
5.5.3 SOM(Self-Organizing Map, 自组织映射)
-
竞争学习型的无监督神经网络,可将高维输入数据映射到低维空间同时保持输入数据在高维空间的拓扑结构,即将高位空间中相似的样本点映射到网络输出层中的邻近神经元。
-
SOM的训练过程:在接收到一个训练样本后,每个输出层神经元会计算该样本与自身携带的权向量之间的距离,距离最近的神经元成为竞争获胜者,称为最佳匹配单元,然后,最佳匹配单元及其邻近神经元的权向量将被调整,以使得这些权向量与当前输入样本的距离缩小,这个过程不断迭代,直至收敛。
5.5.4 级联相关网络 结构自适应网络的重要代表。
一般的神经网络模型通常假定网络结构是事先固定的,训练的目的是利用训练样本来确定合适的连接权、阈值等参数,不同的是结构自适应网络是将网络结构也作为学习的目标之一。
5.5.5 递归神经网络 (recurrent neutral networks)
-
与前馈神经网络不同,recurrent neutral networks允许网络中出现环形结构,从而可让一些神经元的输出反馈回来作为输入信号。
-
Elman网络
常见的递归神经网络之一,结构与多层神经网络相似,但隐层神经元的输出被反馈回来,与下一时刻输入层神经元提供的信号一起,作为隐层神经元在下一时刻的输入。
隐层神经元通常采用sigmoid激活函数,而网络的训练则常通过推广的BP算法进行。
5.5.6 Boltzmann机
- Boltzmann是一种“基于能量的模型”。
- 能量最小化时达到理想状态,网络的训练就是在最小化这个能量函数。
- 常见结构

-
神经元分为两层,显层与隐层。
显层用于表达数据的输入与输出,隐层则被理解为数据的内在表达。 -
Boltzmann机中的神经元都是布尔型的,即只能取0\1(抑制/激活)两种状态(激活、抑制),
- Boltzmann机的训练过程
就是将每个训练样本视为一个状态向量s,使其出现的概率尽可能大。
标准的Boltzmann机是一个全连接图,训练网络的复杂度很高,这使其难以用于解决现实任务
现实中常采用受限Boltzmann机(Restricted Boltzmann Machine,RBM)仅保留显层与隐层之间的连接。
- CD(对比散度 contrastive divergence)算法训练

5.6 深度学习
参数越多,模型复杂度越高。复杂模型训练效率低,易陷入过拟合。但随着云计算大数据时代到来,计算能力的提高,提高了训练效率,训练数据的大幅增加,降低过拟合风险。所以复杂模型----以为代表 ,开始受到关注。
5.6.1 深度学习
典型深度学习:是很深层的神经网络
提高容量:增加隐层数目
模型复杂度:增加隐层神经元数目。但增加隐层数目更有效(因为不仅增加了神经元数目,还增加了激活函数的嵌套层数)
但是增加了层数,就由单隐层变成了多隐层,难以用经典算法例如BP训练,误差在多隐层内逆传播时往往会发散,不能收敛到稳定状态。
- 为了训练多隐层网络,我们用无监督逐层训练
基本思想:
- 预训练
每次训练一层隐结点,将上一层隐结点的输入作为输出 - 微调(fine-tuning)训练
- 例如,深度信念网络deep belief network,DBN每层都是一个受限Boltzmann机,即整个网络可视为若干个RBM堆叠而得,在使用无监督逐层训练时,首先训练第一层,然后将第一层预训练好的隐结点视为第二层的输入结点,对第二层进行预训练,各层训练完成后,再利用BP算法等对整个网络进行训练。
“预训练+微调”的做法可视为将大量参数分组,对每组先找到局部看起来比较好的设置,然后再基于这些局部较优的结果联合起来进行全局寻优。这样就利用了模型大量参数所提供的自由度的同时,有效的节省了训练开销。
- “权共享”(weight sharing)
是另一种节省训练的开销的策略,即让一组神经元使用相同的连接权。这个在卷积神经网络Convolutional Neural Network,CNN中起到重要作用.CNN复合多个“卷积层”和“采样层”对输入信号进行加工,然后在连接层实现与输出目标之间的映射。
无论是DBN还是CNN,
- 其多隐层堆叠、每层对上一层的输出进行处理的机制,可看作是在对输入信号进行逐层加工,
- 从而把初始的、与输出目标之间联系不太密切的输入表示,转化成与输出目标联系更密切的表示
- 使得原来(仅基于最后一层输出映射)难以完成的任务成为可能。
即将低层特征表示转化为高层特征表示,用简单模型完成复杂分类任务。深度学习就是特征学习
6. 支持向量机
6.1 间隔与支持向量
6.1.1 划分超平面
-
分类学习的基本思想:基于训练样本集D = {(x1,y1),(x2,y2),…,(xm,ym}, yi∈{-1,+1},在样本空间找到一个划分超平面,将不同类别样本分开

应找位于两类样本正中间的,对训练样本局部扰动的容忍性最好,产生的分类结果最健壮(鲁棒robust),对未见示例的泛化能力最强。 -
样本空间中任意点x到超平面(w,b)的距离公式推导:

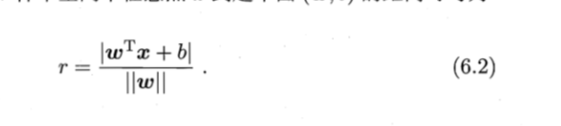
推导过程如下图:

-
正反例分类
该公式被称为最大间隔假设,yi=+1 表示样本为正样本,yi=−1 表示样本为负样本,式子前面选择大于等于+1,小于等于-1只是为了计算方便,原则上可以是任意常数,但无论是多少,都可以通过对 w 的变换使其为 +1 和 -1 。

等价于
- 支持向量
距离超平面最近的,使6.3等号成立的(wTx + b = 1)训练样本点 - 间隔γ(margin):
两个异类支持向量到超平面距离和:
r = ∣ 1 ∣ ∣ ∣ ∗ ∗ w ∗ ∗ ∣ ∣ \frac{|1|}{||**w**||} ∣∣∗∗w∗∗∣∣∣1∣
- 最大间隔的划分超平面(即找使6.3不等式成立的参数w和b使间隔γ最大)

最大化间隔就是最小化||w||,即最小化它的平方,所以重写6.5:
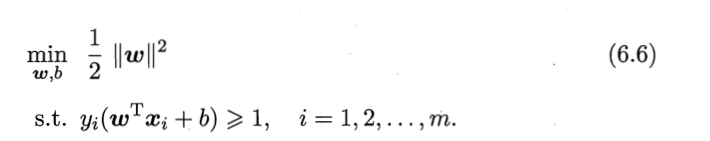
6.2 svm支持向量机
式6.5就是支持向量机的基本型。
关键词:二分类 正确分割 间隔最大化 凸二次规划
1. 支持向量机SVM(support vector machines)
是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。由简至繁的模型包括:
- 当训练样本线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
- 当训练样本近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
- 当训练样本线性不可分时,通过核技巧和软间隔最大化,学习一个非线性支持向量机;
2. 线性可分支持向量机(6.1.1讨论的模型)

现讨论之前未谈及的问题;
- 什么是线性可分
如果一个线性函数能够将样本分开,称这些数据样本是线性可分的。 - 那么什么是线性函数呢?其实很简单,在二维空间中就是一条直线,在三维空间中就是一个平面,以此类推,如果不考虑空间维数,这样的线性函数统称为超平面。
我们看一个简单的二维空间的例子,O代表正类,X代表负类,样本是线性可分的,但是很显然不只有这一条直线可以将样本分开,而是有无数条,我们所说的线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线。
-
那么为什么要间隔最大?

一般来说,一个点距离划分超平面的远近可以表示分类预测的确信度,如图中的A B两个样本点,B点被预测为正类的确信度要大于A点,所以SVM的目标是寻找一个超平面,使得离超平面较近的异类点之间能有更大的间隔,即不必考虑所有样本点,只需让求得的超平面使得离它近的点间隔最大。 -
间隔γ的计算(SVM基本型)前面已讨论得到

-
凸二次规划
该基本型是一个凸二次规划问题,可以采用拉格朗日乘子法(高数中条件极值的求法)对其对偶问题求解求解,
具体来说,对每条约束添加拉格朗日乘子αi≥0(入),则拉格朗日函数为:
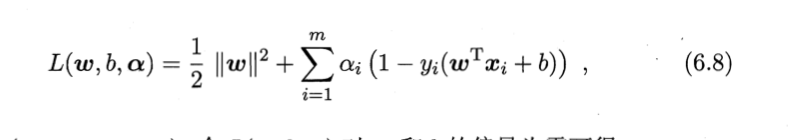

因为是凸二次规划问题,得到6.6的对偶问题


分析一下,对于任意的训练样本 (xi,yi),
- 若 αi=0,则其不会在公式(13)中的求和项中出现,也就是说,它不影响模型的训练;
- 若 αi>0,则yif(xi)−1=0,也就是 yif(xi)=1,即该样本一定在边界上,是一个支持向量。
这里显示出了支持向量机的重要特征:当训练完成后,大部分样本都不需要保留,最终模型只与支持向量有关
3. 非线性支持向量机和核函数(kernel function)
训练样本线性不可分:如异或问题

对于这样的问题,可以将训练样本从原始空间映射到一个更高维的空间,使得样本在这个空间中线性可分。并且如果原始空间维数是有限的,即属性是有限的,那么一定存在一个高维特征空间使样本可分。
令ϕ(x)表示将 x 映射后的特征向量,于是在特征空间中,划分超平面所对应的的模型可表示为:

类似6.6,把x换成φ(x):

得到:

类似6.11,得到对偶问题:


直接计算ϕ(xi)Tϕ(xj)困难,这是样本xi xj映射到特征空间后的内积,于是设想一个函数,将内积等于它们在原始样本空间中通过函数k计算的结果,不必计算高维的内积:

于是带入重写6.21:

同样类似得到模型:
- 这里的函数 κ(xi,xj) 就是核函数,在实际应用中,通常人们会从一些常用的核函数里选择(根据样本数据的不同,选择不同的参数,实际上就得到了不同的核函数)

或者通过函数组合得到:

4.线性支持向量机(软间隔支持向量机)与松弛变量
在前面的讨论中,我们假设训练样本在样本空间或者特征空间中是线性可分的,但在现实任务中往往很难确定合适的核函数使训练集在特征空间中线性可分,退一步说,即使瞧好找到了这样的核函数使得样本在特征空间中线性可分,也很难判断是不是由于过拟合造成。
为解决这一问题,引入软间隔概念
-
软间隔(soft margin)
不要求所有样本满足约束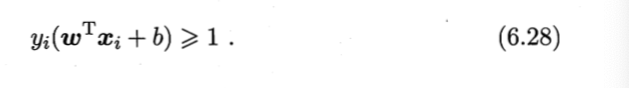
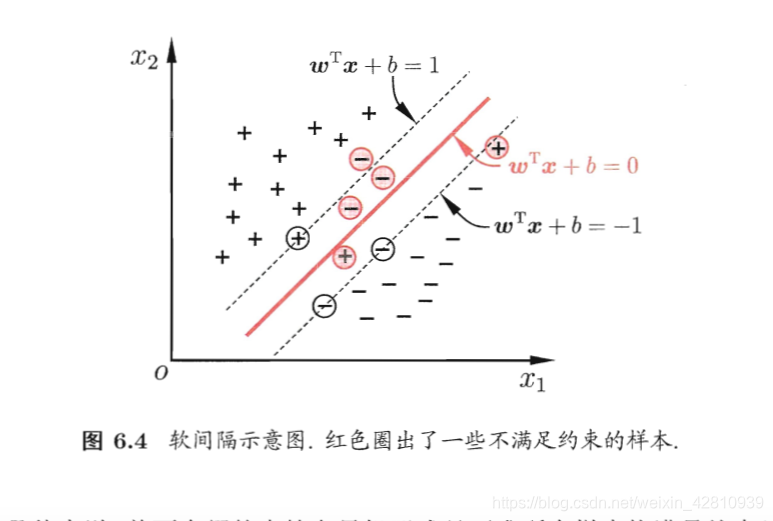
-
优化目标
不满足约束的样本还是应该尽可能少,所以优化目标可写为:

C无穷大式,等价于硬间隔中的6.6目标
C有限值:允许一些样本不满足约束

损失函数数学性质不好,所以找替代损失,通常为凸的连续函数,

采用hinge损失,引入松弛变量


其对偶问题,与线性可分支持向量机的对偶问题解法一致,拉格朗日函数为:


https://blog.youkuaiyun.com/qq_35992440/article/details/80987664
6.3 支持向量回归SVR
对于回归问题,希望学得一个形如6.7的回归模型


6.4 核方法
SVM:

SVR:

- 二者学得的模型总能表示成核函数的线性组合
6.4.1 表示定理(representer theorem)
我们还有更一般的结论:表示定理

- 正则化项Ω要单调递增,不要求为凸函数
- 损失函数
ℓ
\ell
ℓ 无限制
对一般的损失函数,6.57最优解都可以表示成核函数的线性组合
6.4.2 核方法
最常见:核化(引入核函数)把线性学习器拓展为费线性学习器。
以LDA为例通过核化进行非线性拓展,得到核线性判别分析KLDA
类似LDA,把x换成φ


把J作为
e
l
l
ell
ell损失函数,再令正则化项Ω = 0
则h(x)写为
和5.9转化一下,得到w


求解过程类似3.4节LDA

























 1043
1043

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










